Спор о струне

Спор о струне, спор о колеблющейся струне, спор о звучащей струне — научная дискуссия, развернувшаяся в XVIII веке между крупнейшими учёными того времени вокруг изучения колебаний струны. В спор оказались вовлечены Д’Аламбер, Эйлер, Д. Бернулли, Лагранж. Дискуссия касалась определения понятия функции и оказала решающее влияние на множество разделов математики: теорию дифференциальных уравнений в частных производных, математический анализ и теорию функций вещественной переменной, теорию тригонометрических рядов Фурье и теорию обобщённых функций и пространств Соболева.

Возможность теоретического изучения колебаний с точки зрения механики появилась с открытием законов Ньютона (1687) и разработкой анализа бесконечно малых, интегрального и дифференциального исчислений. Однако различные исследования велись и до этого момента Галилеем, Мерсенном, Декартом, Гюйгенсом и др.^[1] В 1625 году Мерсенном была обнаружена зависимость между частотой ${\displaystyle \nu }$, натяжением ${\displaystyle T}$, площадью поперечного сечения ${\displaystyle A}$ и длиной ${\displaystyle l}$ струны, выражающаяся в пропорциональности^[2]

${\displaystyle \nu \propto {\frac {1}{l}}{\sqrt {\frac {T}{A}}}}$

Закон Мерсенна был объяснен теоретически Тейлором почти через столетие, в 1713 году. В его работе исследуется отклонение струны от начального положения, выраженное в виде функции ${\displaystyle y=y(x)}$.

Тейлор полагал, что в любой фиксированный момент времени струна должна иметь форму синусоиды ${\displaystyle y=k\sin(\pi x/l)}$ (что на самом деле оказывается простейшей формой колеблющейся струны)^[2], амплитуда которой зависит от времени, и что при любом начальном условии струна стремится перейти в такое «основное» состояние (что, как оказалось, не соответствует действительности).^[1] Этот подход, иногда называемый «методом стоячих волн», был продолжен Д. Бернулли, однако получил строгое обоснование лишь в работах Фурье.

Тейлор также установил, что сила натяжения, действующая на бесконечно-малый элемент струны и направленная в сторону её отклонения, пропорциональна второй производной ${\displaystyle d^{2}y/dx^{2}}$. В дальнейшем Д’Аламбер стал рассматривать зависимость отклонения не только от пространственной координаты ${\displaystyle x}$, но и от времени ${\displaystyle t}$. Это позволило строго применить второй закон Ньютона, что, однако, потребовало переосмысления природы производной, рассматриваемой Тейлором: она стала частной производной ${\displaystyle \partial ^{2}y/\partial x^{2}}$. Ускорение элемента описывалось другой частной производной: ${\displaystyle \partial ^{2}y/\partial t^{2}}$.

В 1747 году Д’Аламбер переформулировал закон, найденный Тейлором, в терминах дифференциальных уравнений с частными производными и записал уравнение колебания струны в современном виде, называемом волновым уравнением:^[2]

${\displaystyle {\frac {\partial ^{2}y}{\partial t^{2}}}=a^{2}{\frac {\partial ^{2}y}{\partial x^{2}}}.}$

Д’Аламбер применяет следующий подход к решению уравнения колебания струны. Полагая ${\displaystyle a=1}$, он заметил, что при выполнении уравнения колебаний струны справедливо равенство^[3]

${\displaystyle d\left({\frac {\partial y}{\partial x}}\pm {\frac {\partial y}{\partial t}}\right)=\left({\frac {\partial ^{2}y}{\partial t^{2}}}\pm {\frac {\partial ^{2}y}{\partial x\partial t}}\right)(dt\pm dx),}$

и сделал вывод, что коэффициент при дифференциальной форме ${\displaystyle dt\pm dx}$ является функцией от ${\displaystyle (t\pm x)}$ и может быть вычислен интегрированием правой части этого равенства. Это позволяет записать линейную систему на первые частные производные от ${\displaystyle y}$, решение которой даёт полный дифференциал функции ${\displaystyle y}$. Последняя восстанавливается повторным интегрированием. Этот метод позволяет записать решение уравнения колебания струны в виде

${\displaystyle y(t,x)=\phi (t+x)+\psi (t-x),}$

где ${\displaystyle \phi }$ и ${\displaystyle \psi }$ — некоторые произвольные функции, определяемые из начальных условий. Д’Аламбер назвал такое решение общим, подчёркивая, что оно представляет собой целое множество различных решений уравнения^[4].

Аналогичное решение вскоре получил Эйлер, сформулировав то, что мы сейчас назвали бы задачей Коши с заданной начальной формой струны и нулевой начальной скоростью. Выведя уравнение колебания струны и рассматривая его для произвольного ${\displaystyle a}$, он получил решение

${\displaystyle y=\phi (x+at)+\psi (x-at),}$

незначительно отличающееся от решения Д’Аламбера.^[5] В 1766 году Эйлер разрабатывает новый метод, известный сейчас как метод характеристик: переходя к координатам ${\displaystyle u=x+at,v=x-at}$, он записывает исходное уравнение в виде^[5]

${\displaystyle {\frac {\partial ^{2}y}{\partial u\,\partial v}}=0,}$

который легко поддается интегрированию.

Несмотря на то, что Д’Аламбер и Эйлер получили практически одинаковые по форме решения уравнения колебания, они по-разному воспринимали их смысл. Ключевая проблема состояла в том, что полученные решения содержали произвольные функции. Однако общепринятого определения функции на тот момент не было, и среди математиков существовали разные мнения о том, какие функции допустимо рассматривать в анализе, а какие нет. Разногласия по этому вопросу между Д’Аламбером и Эйлером вылились в серию публикаций, начавших спор о струне, к которому впоследствии присоединились другие учёные.^[6]

В зарождающемся математическом анализе XVII—XVIII веков присутствовали два основных подхода: наглядный нестрогий механико-геометрический и формальный алгебраический. С этих двух точек зрения воспринималось и понятие функции. С механистической точки зрения, восходящей к Ньютону и Барроу, функция — это переменная величина, изменяющаяся с течением времени. Последнее в данном случае выступает в качестве аргумента^[7]. Другой подход к функции, восходящий к Ферма и Декарту, но впервые явно сформулированный Иоганном Бернулли (отцом Даниила Бернулли, о котором пойдёт речь ниже), состоит в том, что «функцией переменной величины… называется количество, составленное каким угодно способом из этой переменной величины и постоянных»^[8], то есть некоторая формула, аналитическое выражение от аргумента (не обязательно являющееся аналитической функцией в современном понимании). Класс допустимых операций, с помощью которых можно было получать функции, также варьировался, однако обычно включал в себя арифметические действия, извлечение корня и переходы к пределам, что позволяло рассматривать бесконечные ряды^[9][10]. Первый подход доставлял более широкий класс функций, однако ни строгого определения, ни эффективных методов работы со столь общим понятием функции к середине XVIII в. математики не имели^[11], и в анализе, а также геометрических приложениях исследовались функции, задаваемые одной формулой^[12].

Д’Аламбер рассматривал задачу о струне в первую очередь с позиции чистого математика и не считал своей целью объяснение таких физических эффектов, как гармоническое звучание струны или явление обертонов. Это может показаться несколько странным, но подобный подход к задачам, изначально происходящим из физики, оказался чрезвычайно эффективным в науке XVIII века^[13][14]. Так, рассматривая колебание струны с закрепленными концами и нулевой начальной скоростью, Д’Аламбер записывает решение в виде

${\displaystyle y(t,x)={\frac {1}{2}}(f(x-at)+f(x+at)),}$

полагая при этом, что функция ${\displaystyle f(x)}$, определяющая положение струны в начальной момент времени, должна быть задана каким-то одним правилом, действующим для всех вещественных чисел (чтобы решение было определено для любого момента времени), но таким, чтобы она была нечётной и периодической, с периодом длины 2l (где l — длина струны), что требуется для выполнения граничных условий^[13].

Начальное состояние струны, деформированной на небольшом интервале

анимация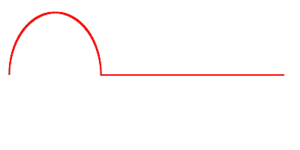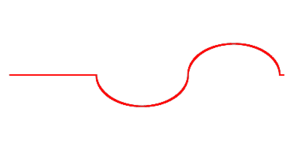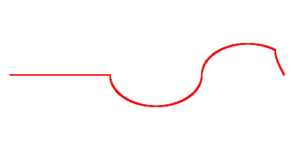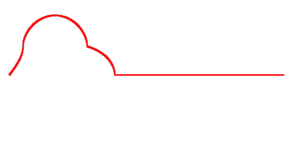

Для Эйлера, напротив, было понятно, что струне в начальный момент времени можно придать форму практически произвольной кривой, начерченной «свободным влечением руки»^[6]. Из физических соображений он предложил рассмотреть функцию, определённую на интервале ${\displaystyle 0\leq x\leq l}$, а затем продолжить эту функцию, пользуясь её нечетностью и периодичностью, на все вещественные числа. Получившийся объект, однако, не был «функцией» в том смысле, который в него вкладывал Д’Аламбер (и даже сам Эйлер ранее)^[15]. Впоследствии Эйлер предлагал также считать, что начальное условие (а, следовательно, и решение) может быть задано не одним аналитическим выражением, а несколькими («кусочно-аналитическое» задание), а впоследствии и вообще отказался от аналитического задания^[6]. В частности, он допускал негладкие функции c «изломами» графика — которые естественно представить себе, рассматривая струну, оттянутую в одной точке^[16].

Начальное состояние струны, оттянутой в одной точке

анимация

Д’Аламбер отмечал, что рассматривать произвольную кривую нельзя, поскольку это «противоречит всем правилам анализа»^[17], и настаивал на том, что начальное условие обязано задаваться одной периодической, нечетной и всюду дифференцируемой функцией^[16]. Отдельной критике подверглось использование функций «с изломами». Д’Аламбер писал, что само уравнения колебания требует, чтобы решение имело как минимум вторые частные производные. Однако если начальное условие имело излом в какой-то точке, то и решение, получемое по найденным формулам, оказывалось негладким в какой-то момент времени в любой наперед заданной точке. Тем самым, оно не могло удовлетворять уравнению в точках изломов^[16]. Здесь особую роль сыграло свойство гиперболических уравнений в частных производных (к которым относится уравнение колебания струны) сохранять гладкость начального условия, а не увеличивать её (что происходит в случае эллиптических уравнений)^[18].

Основной ответ Эйлера на общие возражения состоял в том, что изучение уравнений с частными производными существенно отличается от «обычного анализа» функций одной переменной, где в основном рассматриваются преобразования отдельных аналитических выражений, и нет необходимости рассматривать «смешанные» функции^[19]. Ответ на возражения по поводу негладких решений сводился к тому, что оно будет отличаться от гладкой лишь на «бесконечно-малую» величину, и это различие можно игнорировать — что, конечно, не могло устроить Д’Аламбера^[16]. Другой аргумент состоял в том, что Эйлер предложил «забыть» об исходном уравнении, и считать, что явление описывается найденным общим решением, а не уравнением^[20].

Даниил Бернулли вступил в спор между Эйлером и Д’Аламбером, подвергнув критике их решения с точки зрения физики как чрезвычайно абстрактные. В своих публикациях он отмечал, что это замечательные математические результаты, но спрашивал: «при чём здесь звучащие струны?»^[21].

Исходя из представлений о природе колебаний, он развивает идею о важной роли «чистых колебаний» синусоидальной формы, появившуюся ещё у Тейлора. Его догадка заключалась в том, что произвольное колебание может быть представлено как «наложение», или сумма, нескольких чистых колебаний (принцип суперпозиции), что соответствовало наблюдением за струной: издаваемый ею звук состоит из основного тона и множества обертонов. Бернулли нашёл решение уравнения колебания в виде суммы тригонометрического ряда и утверждал (опять же исходя из физических соображений), что таким рядом можно представить произвольную функцию. Это предположение он не мог подтвердить математически — в частности, он не знал формулы для вычисления коэффициентов такого ряда. Тем не менее он полагал, что его решение не только имеет бо́льший физический смысл, чем решения Д’Аламбера и Эйлера, но и является более общим^[22].

В то время ряды были важным объектом изучения, и многие математики (включая Ньютона) рассматривали степенные ряды (с вещественными показателями степеней) как универсальный способ записи произвольных функций^[23]. Однако необходимого уровня понимания тригонометрического ряда на тот момент достигнуто не было, и ни Д’Аламбер, ни Эйлер не согласились с тем, что тригонометрический ряд способен описывать достаточно широкий класс функций. Это непонимание усиливалось распространенным тогда представлением, что если два аналитических выражения совпадают на каком-то участке числовой оси, то они совпадают всюду. Так, Эйлер не мог поверить в то, что тригонометрическим рядом можно описать поведение струны, возмущённой только на небольшом участке. Возражения также вызывало требование периодичности функции, представимой в виде ряда, естественно следующее из периодичности слагаемых^[24][25].

Лишь в много более поздних работах Фурье (начало XIX века) было показано, что даже недоступные для описания степенным рядом (и не являющиеся аналитическими в современном понимании) функции с изломами могут быть представлены на некотором отрезке тригонометрическим рядом. Дальнейшие исследования вопросов сходимости рядов Фурье привели Кантора к построению теории множеств и в конечном итоге к появлению современного функционального анализа^[26].

Результаты Фурье ответили на один из ключевых вопросов в споре о струне: о представимости широкого класса функций тригонометрическим рядом. Однако другой источник разногласий — парадокс, связанный с возможностью негладкости начальных условий, а, следовательно, и решений — оставался открытым не только в XVIII, но и в XIX веке. Он был разрешён только в XX веке с появлением аппарата обобщённых функций (распределений)^[6]. Основы этой теории были заложены в конце 1936 года С. Л. Соболевым в результате исследования задачи Коши для гиперболических уравнений (к которым относится и уравнение колебания струны) и в дальнейшем строго развиты Лораном Шварцем в 1950-х годах^[27].

Идея состоит в замене уравнения колебания на эквивалентное ему (в некотором смысле) интегральное уравнение, решение которого ищется уже не в классе дважды гладких функций, а в так называемых соболевских пространствах, представляющих собой пополнение пространства непрерывных функций по некоторой специальной метрике. Можно также считать, что производные негладкой функции, стоящие в левой части уравнения колебания струны, являются обобщённой функцией, и равенство справедливо в смысле обобщённых функций^[28].

• История математики с древнейших времен до начала XIX столетия / Под ред. А. П. Юшкевича. — М.: Наука, 1970. — Т. II, математика XVII столетия. — 300 с.
• История математики с древнейших времен до начала XIX столетия / Под ред. А. П. Юшкевича. — М.: Наука, 1972. — Т. III, математика XVIII столетия. — 495 с.
• Стиллвелл, Дж. Математика и её история. — Ижевск: Институт компьютерных исследований/РХД, 2004. — 530 с.
• Wheeler, G. F., Crummett W. P. The vibrating string controversy // American Journal of Physics. — American Association of Physics Teachers, 1987. — Vol. 55, № 1. — P. 33—37. — doi:10.1119/1.15311.
• Christensen, T. Eighteenth-Century Science and the Corps Sonore: the Scientific Background to Rameau’s Principle of Harmony // Journal of Music Theory. — 1987. — Vol. 31. — P. 23—50.
• Ravetz J. R. Vibrating Strings and Arbitrary Functions // The Logic of Personal Knowledge: Essays Presented to M. Polanyi on his Seventieth Birthday. — London: Routledge, 1961. — P. 71—88.
• Kleiner, I. Evolution of the function concept: A brief survey // The College Mathematics Journal. — 1989. — Vol. 20. — P. 282—300.
• Ларин А. А. Зарождение математической физики и теории колебаний континуальных систем в «Споре о струне» // Вестник Национального технического университета «Харьковский политехнический институт». История науки и техники. — 2008. — № 8.