Уравнение Дира́ка — релятивистски инвариантное уравнение движения для биспинорного классического поля электрона, применимое также для описания других точечных фермионов со спином 1/2; установлено Полем Дираком в 1928 году.
Моме́нт и́мпульса — векторная физическая величина, характеризующая количество вращательного движения и зависящая от того, сколько массы вращается, как она распределена в пространстве и с какой угловой скоростью происходит вращение.

Теоре́ма Нётер или первая теорема Нётер утверждает, что каждой дифференцируемой симметрии действия для физической системы с консервативными силами соответствует закон сохранения. Теорема была доказана математиком Эмми Нётер в 1915 году и опубликована в 1918 году. Действие для физической системы представляет собой интеграл по времени функции Лагранжа, из которого можно определить поведение системы согласно принципу наименьшего действия. Эта теорема применима только к непрерывным и гладким симметриям над физическим пространством.
Краевая задача — задача о нахождении решения заданного дифференциального уравнения, удовлетворяющего краевым (граничным) условиям в концах интервала или на границе области. Краевые задачи для гиперболических и параболических уравнений часто называют начально-краевыми или смешанными, потому что в них задаются не только граничные, но и начальные условия.

Фу́нкция Гри́на — функция, используемая для решения линейных неоднородных дифференциальных уравнений с граничными условиями . Названа в честь английского математика Джорджа Грина, который первым развил соответствующую теорию в 1830-е годы.
Лагранжева механика — формулировка классической механики, введённая Луи Лагранжем в 1788 году. В лагранжевой механике траектория объекта получается при помощи отыскания пути, который минимизирует действие — интеграл от функции Лагранжа по времени. Функция Лагранжа для классической механики вводится в виде разности между кинетической энергией и потенциальной энергией.
Дифференциа́льное уравне́ние в ча́стных произво́дных — дифференциальное уравнение, содержащее неизвестные функции нескольких переменных и их частные производные.
Характеристи́ческая фу́нкция случа́йной величины́ — один из способов задания распределения. Характеристические функции могут быть удобнее в тех случаях, когда, например, плотность или функция распределения имеют очень сложный вид. Также характеристические функции являются удобным инструментом для изучения вопросов слабой сходимости. В теорию характеристических функций внесли большой вклад Ю. В. Линник, И. В. Островский, К. Р. Рао, Б. Рамачандран.
Те́нзор эне́ргии-и́мпульса (ТЭИ) — симметричный тензор второго ранга (валентности), описывающий плотность и поток энергии и импульса полей материи и определяющий взаимодействие этих полей с гравитационным полем.
Волновое уравнение в физике — линейное гиперболическое дифференциальное уравнение в частных производных, задающее малые поперечные колебания тонкой мембраны или струны, а также другие колебательные процессы в сплошных средах и электромагнетизме (электродинамике). Находит применение и в других областях теоретической физики, например при описании гравитационных волн. Является одним из основных уравнений математической физики.
Эллипти́ческий интегра́л — некоторая функция  над полем действительных или комплексных чисел, которая может быть формально представлена в следующем виде:
над полем действительных или комплексных чисел, которая может быть формально представлена в следующем виде:
 ,
,
Фо́ккера-Пла́нка приближе́ние — описание физической кинетики частиц в газе в случае, когда распределение частиц по скоростям имеет почти изотропный характер. В основном применяется для описания электронов в газах при воздействии электрического поля.
Гипергеометри́ческая фу́нкция — одна из специальных функций. Определяется внутри круга  как сумма гипергеометрического ряда
как сумма гипергеометрического ряда

Задача Кеплера вообще представляет собой проблему отыскания движения двух сферически-симметричных тел, взаимодействующих гравитационно. В классической теории тяготения решение этой проблемы было найдено самим Исааком Ньютоном: оказалось, что тела будут двигаться по коническим сечениям, в зависимости от начальных условий — по эллипсам, параболам или гиперболам. В рамках общей теории относительности (ОТО) с пуристической точки зрения эта задача представляется плохо поставленной, так как модель абсолютно твёрдого тела невозможна в релятивистской физике, а не абсолютно твёрдые тела не будут при взаимодействии сферически-симметричными. Другой подход включает переход к точечным телам, правомерный в ньютоновской физике, но вызывающий проблемы в ОТО. Помимо этого, кроме положений и скоростей тел необходимо задать также и начальное гравитационное поле (метрику) во всём пространстве — проблема начальных условий в ОТО. В силу указанных причин точного аналитического решения задачи Кеплера в ОТО не существует, но есть комплекс методов, позволяющих рассчитать поведение тел в рамках данной задачи с необходимой точностью: приближение пробного тела, постньютоновский формализм, численная относительность.

Спонта́нное наруше́ние симме́три́и — способ нарушения симметрии физической системы, при котором исходное состояние и уравнения движения системы инвариантны относительно некоторых преобразований симметрии, но в процессе эволюции система переходит в состояние, для которого инвариантность относительно некоторых преобразований начальной симметрии нарушается. Спонтанное нарушение симметрии всегда связано с вырождением состояния с минимальной энергией, называемого вакуумом. Множество всех вакуумов имеет начальную симметрию, однако каждый вакуум в отдельности — нет. Например, шарик в жёлобе с двумя ямами скатывается из неустойчивого симметричного состояния в устойчивое состояние с минимальной энергией либо влево, либо вправо, разрушая при этом симметрию относительно изменения левого на правое.
Эллипсоидальные координаты — трёхмерная ортогональная система координат  , являющаяся обобщением двумерной эллиптической системы координат. Данная система координат основана на использовании софокусных поверхностей второго порядка.
, являющаяся обобщением двумерной эллиптической системы координат. Данная система координат основана на использовании софокусных поверхностей второго порядка.
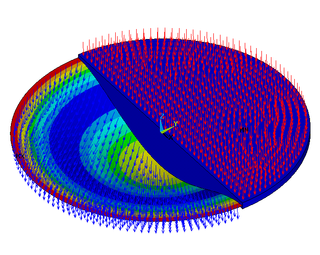
Изгиб пластин в теории упругости относится к расчёту деформаций в пластинах, под действием перпендикулярных к плоскости пластины внешних сил и моментов. Величину отклонения можно определить, решив дифференциальные уравнения соответствующей теории пластин в зависимости от допущений на малость тех или иных параметров. По этим прогибам можно рассчитать напряжения в пластине. При известных напряжениях можно использовать теорию разрушения, чтобы определить, нарушение целостности плиты при данной нагрузке. Деформация пластины является функцией двух координат, поэтому теория пластин формулируется в общем случае в терминах дифференциальных уравнений в двумерном пространстве. Также считается, что пластина изначально имеет плоскую форму.
Комплексная дифференциальная форма — дифференциальная форма с комплексными коэффициентами, обычно рассматривается на комплексных многообразиях.
























