Основна́я теоре́ма а́лгебры — утверждение о том, что поле комплексных чисел алгебраически замкнуто, то есть что всякий отличный от константы многочлен с комплексными коэффициентами имеет по крайней мере один корень в поле комплексных чисел. Утверждение справедливо и для многочленов с вещественными коэффициентами, так как всякое вещественное число является комплексным с нулевой мнимой частью.
Теорема Декарта или правило знаков Декарта, — теорема, утверждающая, что число положительных корней многочлена с вещественными коэффициентами равно числу перемен знаков в ряду его коэффициентов или на чётное число меньше этого числа.

Рациона́льная фу́нкция, или дро́бно-рациона́льная фу́нкция, или рациона́льная дробь — это числовая функция, которая может быть представлена в виде дроби, числителем и знаменателем которой являются многочлены. К этому виду может быть приведено любое рациональное выражение, то есть алгебраическое выражение, без радикалов.
Дискримина́нт многочлена — математическое понятие, обозначаемое буквами D или Δ.
Ко́мпле́ксный ана́лиз, тео́рия фу́нкций ко́мпле́ксного переме́нного — раздел математического анализа, в котором рассматриваются и изучаются функции комплексного аргумента.
Неприводимый многочлен — многочлен, неразложимый на нетривиальные многочлены. Неприводимые многочлены являются неприводимыми элементами кольца многочленов.
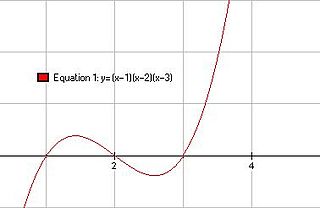
Корень многочлена

Теоре́ма Ра́уса — Гу́рвица предоставляет возможность определить, является ли данный многочлен устойчивым по Гурвицу. Была доказана в 1895 г. А. Гурвицем и названа в честь Э. Дж. Рауса и А. Гурвица.
Интегральная формула Коши — соотношение для голоморфных функций комплексного переменного, связывающее значение функции в точке с её значениями на контуре, окружающем точку.
Теоре́ма Ги́льберта о нуля́х — теорема, устанавливающая фундаментальную взаимосвязь между геометрией и алгеброй. Использование этой взаимосвязи является основой алгебраической геометрии.

Теорема Тейлора даёт приближение к функции, дифференцируемой k раз, вблизи данной точки с помощью многочлена Тейлора k-го порядка. Для аналитических функций многочлен Тейлора в данной точке является частичной суммой их ряда Тейлора, который, в свою очередь, полностью определяет функцию в некоторой окрестности точки. Точное содержание теоремы Тейлора до настоящего времени не согласовано. Конечно, существует несколько версий теоремы, применимых в различных ситуациях, и некоторые из этих версий содержат оценки ошибки, возникающей при приближении функции с помощью многочлена Тейлора.
Алгоритм вычисления собственных значений — алгоритм, позволяющий определить собственные значения и собственные векторы заданной матрицы. Создание эффективных и устойчивых алгоритмов для этой задачи является одной из ключевых задач вычислительной математики.
Комбинаторная теорема о нулях — алгебраическая теорема, связывающая коэффициент многочлена при определённом одночлене с его значениями. Теорема даёт нижнюю оценку на размеры комбинаторного параллелепипеда, на котором многочлен не равен тождественно нулю. Эта оценка зависит от степени старшего одночлена по каждой переменной.
Выразимость в радикалах означает возможность выразить число или функцию через простейшие числа или функции при помощи извлечения корня целой степени и арифметических операций — сложения, вычитания, умножения, деления.







































