Фундамента́льная гру́ппа — одна из простейших конструкций в алгебраической топологии. Сопоставляется группа всякому связному топологическому пространству. Для подмножеств плоскости эта группа измеряет количество «дырок». Наличие «дырки» определяется невозможностью непрерывно продеформировать (стянуть) некоторую замкнутую кривую в точку.
Алгебраи́ческая тополо́гия — раздел топологии, изучающий топологические пространства путём сопоставления им алгебраических объектов, а также поведение этих объектов под действием различных топологических операций.
В этом глоссарии приведены определения основных терминов, используемых в общей топологии. Курсивом выделены ссылки внутри глоссария.
В математике, если заданы две группы (G, ∗) и (H, •), гомоморфизм групп из (G, ∗) в (H, •) — это функция h : G → H, такая, что для всех u и v из G выполняется
Функтор — особый тип отображений между категориями. Его можно понимать как отображение, сохраняющее структуру. Функторы между малыми категориями являются морфизмами в категории малых категорий. Совокупность всех категорий не является категорией в обычном смысле, так как совокупность её объектов не является классом. Один из способов преодолеть подобные теоретико-множественные трудности — добавление в ZFC независимой от неё аксиомы о существовании недостижимых кардиналов.
Локально тривиальное расслоение — расслоение, которое локально выглядит как прямое произведение.
Теория гомоло́гий — раздел математики, который изучает конструкции некоторых топологических инвариантов, называемых группами гомологий и группами когомологий. Также теориями гомологий называют конкретные конструкции групп гомологий.
Гомотопи́ческие гру́ппы — инвариант топологических пространств, одно из основных понятий алгебраической топологии.
Теорема Зейферта — ван Кампена выражает фундаментальную группу топологического пространства через фундаментальные группы двух открытых подмножеств, покрывающих пространство.
Гомотопические группы сфер — один из основных объектов изучения теории гомотопий, области алгебраической топологии. Гомотопические группы сфер классифицируют отображения между многомерными сферами с точностью до непрерывной деформации. Гомотопические группы сфер являются дискретными алгебраическими объектами, а именно конечнопорождёнными абелевыми группами. Несмотря на то, что классификация конечнопорождённых абелевых групп очень проста, точная структура гомотопических групп сфер до конца неизвестна.
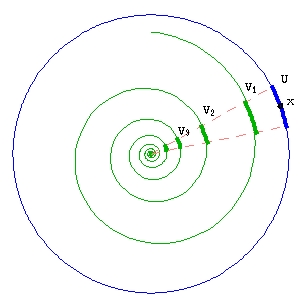
В математике монодро́ми́ей называется явление, состоящее в преобразовании некоторого объекта при обнесении его вдоль нетривиального замкнутого пути.
Фуксова модель — это представление гиперболической римановой поверхности R как факторповерхности верхней полуплоскости H по фуксовой группе. Любая гиперболическая риманова поверхность позволяет такое представление. Концепция названа именем Лазаря Фукса.
Асферическое пространство — топологическое пространство в котором все гомотопические группы 
кроме 
тривиальны. Для симплектических многообразий значение термина немного отличается; смотри симплектически асферическое многообразие.
Трёхмерное многообразие — топологическое пространство, локально устроенное как трёхмерное евклидово пространство 
. Иными словами, многообразие размерности три. Является центральным понятием трёхмерной топологии.
Абелианиза́ция — способ превратить произвольную группу в абелеву. Является полезным инструментом в теории групп, который находит применение в алгебраической топологии.
Первая группа гомологий топологического пространства — абелева группа, состоящая из петель в этом пространстве, рассматриваемых с точностью до гомологичности. Такие петли описывают форму пространства и измеряют количество его дыр. Первая группа гомологий является простейшим вариантом групп гомологий топологического пространства — одного из центральных понятий теории гомологий и алгебраической топологии.
Первая группа когомологий топологического пространства — абелева группа, состоящая из аддитивных целозначных функций на первой группе гомологий этого пространства. Она является простейшим вариантом групп когомологий — одного из центральных понятий теории гомологий и алгебраической топологии.
![{\displaystyle {\tilde {h}}_{*}\colon \pi _{1}(X)/[\pi _{1}(X),\pi _{1}(X)]\to H_{1}(X)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e5c24681eed4f201336b16ca897642127928f9bb)
