Теорема Жордана — Гёльдера

Теорема Жордана — Гёльдера гласит:

Если у группы $\displaystyle G$ существует композиционный ряд $\{1\}=G_{0}\varsubsetneq G_{1}\varsubsetneq \cdots \varsubsetneq G_{n}=G$ , то его длина $\displaystyle n$ и все факторы $\displaystyle G_{i+1}/G_{i}$ определены однозначно, с точностью до перестановок и изоморфизмов^[1].

Это классический вариант теоремы Жордана — Гёльдера. Он относится к случаю, когда композиционный ряд конечен, то есть включает конечное число подгрупп группы $\displaystyle G$ . Теорема Жордана — Гёльдера остается справедливой и в случае восходящих трансфинитных композиционных рядов^[2].

Литература

↑ Винберг Э. Б. Курс алгебры. — 3-е изд. — М.: Факториал Пресс, 2002. — ISBN 5-88688-0607.
↑ Sharipov, R.A. (2009). "Transfinite normal and composition series of groups". arXiv:0908.2257 [math.GR].

См. также

Простая группа

Похожие исследовательские статьи

Алгебраи́ческая тополо́гия — раздел топологии, изучающий топологические пространства путём сопоставления им алгебраических объектов, а также поведение этих объектов под действием различных топологических операций.

Ряд Фурье́ — представление функции $\text{[math]}$ с периодом $\text{[math]}$ в виде ряда

\text{[math]}

Крива́я или ли́ния — геометрическое понятие, определяемое в разных разделах математики различно.

В этой статье приведены основные термины, используемые в теории групп. Курсив обозначает внутреннюю ссылку на данный глоссарий. В конце приводится таблица основных обозначений, применяемых в теории групп.

Симметрическая группа — группа всех перестановок заданного множества $\text{[math]}$ относительно операции композиции.

Преобразование Фурье́ — операция, сопоставляющая одной функции вещественной переменной другую функцию вещественной переменной. Эта новая функция описывает коэффициенты («амплитуды») при разложении исходной функции на элементарные составляющие — гармонические колебания с разными частотами.

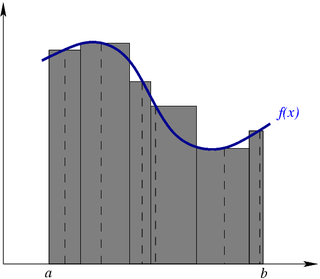
<span class="mw-page-title-main">Интеграл Римана</span> простейшее определение интеграла

Интегра́л Ри́мана — наиболее широко используемый вид определённого интеграла. Очень часто под термином «определённый интеграл» понимается именно интеграл Римана, и он изучается самым первым из всех определённых интегралов во всех курсах математического анализа. Введён Бернхардом Риманом в 1854 году, и является одной из первых формализаций понятия интеграла.

Мера Жордана — один из способов формализации понятия длины, площади и $\text{[math]}$ -мерного объёма в $\text{[math]}$ -мерном евклидовом пространстве.

Теорема Жордана — классическая теорема топологии, гласящая, что замкнутая плоская кривая без самопересечений делит плоскость на две различные части: «внутреннюю» и «внешнюю».

<span class="mw-page-title-main">Жордан, Мари Энмон Камиль</span> французский математик

Мари́ Энмо́н Ками́ль (Камилл) Жорда́н — французский математик, известный благодаря своим фундаментальным работам в теории групп и «Курсу анализа». Он родился в Лионе и учился в Политехнической школе. По образованию Жордан был инженером; позже он преподавал в Политехнической школе и Коллеж де Франс.

Ко́мпле́ксный ана́лиз, тео́рия фу́нкций ко́мпле́ксного переме́нного — раздел математического анализа, в котором рассматриваются и изучаются функции комплексного аргумента.

Вы́чет в комплексном анализе — объект, характеризующий локальные свойства заданной функции или формы.

Нера́венство Гёльдера в функциональном анализе и смежных дисциплинах — это фундаментальное свойство пространств $\text{[math]}$ .

В теории динамических систем, пример Данжуа — пример $\text{[math]}$ -диффеоморфизма окружности с иррациональным числом вращения, имеющего канторово инвариантное множество. М. Эрманом были затем построены примеры такого диффеоморфизма в классе гладкости $\text{[math]}$ для любого $\text{[math]}$ . Эта гладкость не может быть далее увеличена: для диффеоморфизмов с липшицевой производной имеет место теорема Данжуа, утверждающая, что такой диффеоморфизм с иррациональным числом вращения сопряжён иррациональному повороту.

Теорема о классификации простых конечных групп — теорема теории групп, классифицирующая с точностью до изоморфизма простые конечные группы.

В математике ряд подгрупп — это цепь подгрупп вида $\text{[math]}$ . Ряды подгрупп могут упростить изучение группы $\text{[math]}$ сводя его к изучению подгрупп этой группы и к изучению взаимосвязей между ними. Ряды подгрупп могут формировать важные инварианты заданной группы $\text{[math]}$ .

<span class="mw-page-title-main">Гёльдер, Отто</span> немецкий математик

Отто Людвиг Гёльдер — немецкий математик, родился в Штутгарте. Наиболее известен по неравенству Гёльдера, условию Гёльдера и теореме Жордана — Гёльдера, среди других известных результатов — теорема Гёльдера о том, что гамма-функция не удовлетворяет никакому линейному дифференциальному уравнению с рациональными коэффициентами, а также доказательство совершенности симметрических групп $\text{[math]}$ при $\text{[math]}$ .

Центр группы в теории групп — множество всех таких элементов данной группы, которые коммутируют со всеми её элементами:

\text{[math]}

Теорема Гёльдера — одно из утверждений, связанных с немецким математиком Отто Гёльдером. Возможные значения:

Теорема Гёльдера в анализе — утверждение о том, что гамма-функция не удовлетворяет никакому линейному дифференциальному уравнению с рациональными коэффициентами.
Теорема Гёльдера в теории групп — утверждение о совершенности симметрических групп $\text{[math]}$ при $\text{[math]}$ .
Теорема Гёльдера в теории упорядоченных групп — утверждение о том, что всякая архимедова упорядоченная группа коммутативна и у-изоморфна подгруппе аддитивной группы вещественных чисел.
Теорема Жордана — Гёльдера.

Упорядоченная группа — группа, для всех элементов которой определён линейный порядок, согласованный с групповой операцией. Вообще говоря, группа может быть не коммутативной.

Эта страница основана на статье Википедии.
Текст доступен на условиях лицензии CC BY-SA 4.0; могут применяться дополнительные условия.
Изображения, видео и звуки доступны по их собственным лицензиям.