Теорема Косниты

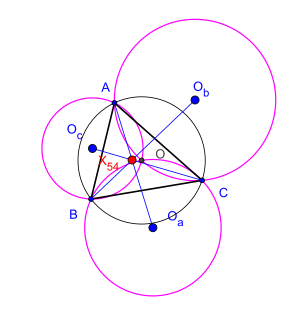
Теорема Косниты — это свойство некоторых окружностей, связанных с произвольным треугольником.

Пусть $ABC$ — произвольный треугольник, $O$ — центр его описанной окружности, а $O_{a},O_{b},O_{c}$ — центры описанных окружностей трёх треугольников $OBC$ , $OCA$ и $OAB$ соответственно. Теорема утверждает, что три прямых $AO_{a}$ , $BO_{b}$ и $CO_{c}$ пересекаются в одной точке ^[1]. Этот факт был установлен Румынским математиком Цезарем Коснита (Cezar Coşniţă, 1910-1962) ^[2].

Точка, в которой прямые пересекаются, известна как точка Косниты треугольника (название дал Ригби в 1997). Точка является изогонально сопряжённой центру девяти точек^[3]^[4]. Точка имеет обозначение $X(54)$ среди замечательных точек треугольника в списке Кимберлинга^[5]. Теорема является частным случаем теоремы Дао о 6 центрах описанных окружностей для вписанного шестиугольника^[6]^[7]^[8]^[9].

Свойства

Треугольник T с вершинами A, B и C; O — центр описанной окружности (красная).
A*, B* и C* — точки, симметричные точкам A, B и C относительно противоположной стороны.
M — точка пересечения окружностей Массельмана.
Зелёная окружность — окружность девяти точек, N — её центр.
K — точка Коснита.

Точка Косниты K тесно связана с точкой M Массельмана (с точкой пересечения окружностей Массельмана). См. рис. и теорему Массельмана. Точка Массельмана $M$ является точкой инверсии точки Косниты относительно окружности, описанной вокруг треугольника $T$ .

↑ Weisstein, Eric W. Kosnita Theorem (англ.) на сайте Wolfram MathWorld.
↑ Ion Pătraşcu (2010), A generalization of Kosnita's theorem Архивная копия от 10 мая 2017 на Wayback Machine (in Romanian)
↑ Grinberg, 2003, с. 105–111.
↑ Rigby, 1997, с. 156-158.
↑ Clark Kimberling (2014), Encyclopedia of Triangle Centers Архивная копия от 19 апреля 2012 на Wayback Machine, section X(54) = Kosnita Point. Accessed on 2014-10-08
↑ Dergiades, 2014, с. 243–246.
↑ Cohl, 2014, с. 261–264.
↑ Duong, 2016, с. 25-39.
↑ X(3649) = KS(INTOUCH TRIANGLE) (неопр.). Дата обращения: 7 февраля 2017. Архивировано 26 апреля 2017 года.

Литература

John Rigby. Brief notes on some forgotten geometrical theorems // Mathematics and Informatics Quarterly. — 1997. — Т. 7. — С. 156-158. (как процитировано у Кимберлинга).
Darij Grinberg. On the Kosnita Point and the Reflection Triangle // Forum Geometricorum^[англ.]. — 2003. — Т. 3. — С. 105–111.
Nikolaos Dergiades. Dao’s Theorem on Six Circumcenters associated with a Cyclic Hexagon // Forum Geometricorum^[англ.]. — 2014. — Т. 14. — С. 243–246. — ISSN 1534-1178.
Telv Cohl. A purely synthetic proof of Dao's theorem on six circumcenters associated with a cyclic hexagon // Forum Geometricorum^[англ.]. — 2014. — Т. 14. — С. 261–264. — ISSN 1534-1178.
Ngo Quang Duong. Some problems around the Dao's theorem on six circumcenters associated with a cyclic hexagon configuration // International Journal of Computer Discovered Mathematics. — 2016. — Т. 1. — С. 25-39. — ISSN 2367-7775.

Похожие исследовательские статьи

<span class="mw-page-title-main">Теорема Фейербаха</span> окружность девяти точек касается вписанной и вневписанных окружностей

Теорема Фейербаха — результат геометрии треугольника. Теорема была сформулирована и доказана Карлом Вильгельмом Фейербахом в 1822 году.

<span class="mw-page-title-main">Ортоцентр</span> точка пересечения высот треугольника

Ортоцентр — точка пересечения высот треугольника или их продолжений. Традиционно обозначается латинской буквой $\text{[math]}$ . В зависимости от вида треугольника ортоцентр может находиться внутри треугольника, вне его или совпадать с вершиной. Ортоцентр относится к замечательным точкам треугольника и перечислен в энциклопедии центров треугольника Кларка Кимберлинга как точка X(4).

Серединный треугольник — треугольник, построенный на серединах сторон данного треугольника, частный случай серединного многоугольника.

Прямая Симсона — прямая, проходящая через основания перпендикуляров на стороны треугольника из точки на его описанной окружности. Её существование опирается на теорему Симсона.

Теорема Наполеона — утверждение евклидовой планиметрии о равносторонних треугольниках:

Если на каждой стороне произвольного треугольника построить по равностороннему треугольнику, то треугольник с вершинами в центрах равносторонних треугольников — тоже равносторонний

Формула Эйлера — теорема планиметрии, связывает расстояние между центрами вписанной и описанной окружностей и их радиусами.

Вписанная в треугольник окружность — окружность внутри треугольника, касающаяся всех его сторон; наибольшая окружность, которая может находиться внутри треугольника. Центр этой окружности является точкой пересечения биссектрис треугольника и называется инцентром треугольника.

В евклидовой геометрии описанный четырёхугольник — это выпуклый четырёхугольник, стороны которого являются касательными к одной окружности внутри четырёхугольника. Эта окружность называется вписанной в четырёхугольник. Описанные четырёхугольники являются частным случаем описанных многоугольников.

Вписанный четырёхугольник — это четырёхугольник, вершины которого лежат на одной окружности. Эта окружность называется описанной. Обычно предполагается, что четырёхугольник выпуклый, но бывают и самопересекающиеся вписанные четырёхугольники. Формулы и свойства, данные ниже, верны только для выпуклых четырёхугольников.

Набор окружностей Джонсона состоит из трёх окружностей одинакового радиуса r, имеющих одну общую точку пересечения H. В такой конфигурации окружности обычно имеют четыре точки пересечения — это общая точка пересечения H, через которую проходят все три окружности, и по дополнительной точке для каждой пары окружностей. Если любые две окружности не пересекаются они имеют лишь одну общую точку — H, и в этом случае считается, что H является и их попарной точкой пересечения также. Если же окружности совпадают, принимается за попарную точку пересечения точка, диаметрально противоположная точке H. Три точки попарных пересечений окружностей Джонсона образуют опорный треугольник Δ ABC фигуры. Конфигурация названа именем Роджера Артура Джонсона.

Центр окружности девяти точек — одна из замечательных точек треугольника. Её часто обозначают как $\text{[math]}$ .

Центр Шпикера — замечательная точка треугольника, определяемая как центр масс периметра треугольника; то есть центр тяжести однородной проволоки, проходящей по периметру треугольника.

Теорема Лестера — утверждение в геометрии треугольника, согласно которому в любом разностороннем треугольнике две точки Ферма, центр девяти точек и центр описанной окружности лежат на одной окружности. Названа именем канадского математика Джун Лестер.

В евклидовой геометрии теорема Массельмана — это свойство некоторых окружностей, определённых для произвольного треугольника.

Точка Шиффлера — замечательная точка треугольника, являющаяся пересечением прямых Эйлера четырёх треугольников $\text{[math]}$ , $\text{[math]}$ , $\text{[math]}$ , $\text{[math]}$ , где $\text{[math]}$ — инцентр $\text{[math]}$ . Теорема Шиффлера утверждает, что эти четыре линии действительно пересекаются в одной точке.

Центральные прямые — это некоторые специальные прямые, связанные с треугольником и лежащие в плоскости треугольника. Особое свойство, которое отличает прямые как центральные прямые, проявляется через уравнение прямой в трилинейных координатах. Это особое свойство также связано с понятием центр треугольника. Понятие центральной прямой было введено Кларком Кимберлингом в статье, опубликованной в 1994 году.

Японская теорема о вписанном четырёхугольнике утверждает, что центры окружностей, вписанных в определённые треугольники внутри вписанного в окружность четырёхугольника, являются вершинами прямоугольника.

<span class="mw-page-title-main">Конциклические точки</span>

Конциклические точки — точки, находящиеся на одной окружности. Три точки на плоскости, не лежащие на одной прямой, всегда лежат на одной окружности, поэтому иногда термин «конциклические» прилагают только к наборам из 4 или более точек.

В планиметрии окружность Ламуна — это специальная окружность, которую можно построить в любом треугольнике $\text{[math]}$ . Она содержит центры описанных окружностей шести треугольников, на которые треугольник $\text{[math]}$ разрезают три его медианы. Пусть для определенности $\text{[math]}$ , $\text{[math]}$ , $\text{[math]}$ — 3 вершины треугольника $\text{[math]}$ , и пусть $\text{[math]}$ — его центроид. Пусть $\text{[math]}$ , $\text{[math]}$ и $\text{[math]}$ — середины сторон $\text{[math]}$ , $\text{[math]}$ и $\text{[math]}$ соответственно. Тогда центры шести описанных окружностей шести треугольников, на которые треугольник разбивается медианами: $\text{[math]}$ , $\text{[math]}$ , $\text{[math]}$ , $\text{[math]}$ , $\text{[math]}$ и $\text{[math]}$ , лежат на общей окружности, которая называется окружностью Ламуна.

<span class="mw-page-title-main">Точка Фейербаха</span> точка касания окружности девяти точек и вписанной окружности треугольника

Точка Фейербаха — точка касания вписанной окружности к окружности девяти точек треугольника. Точка Фейербаха является касательной точкой треугольника, что означает то, что её определение не зависит от расположения и размеров треугольника. Точка внесена с кодом X(11) в энциклопедию центров треугольника Кларка Кимберлинга и названа именем Карла Вильгельма Фейербаха.

Эта страница основана на статье Википедии.
Текст доступен на условиях лицензии CC BY-SA 4.0; могут применяться дополнительные условия.
Изображения, видео и звуки доступны по их собственным лицензиям.