Теорема Манна — Вальда

Теорема Манна — Вальда (англ. Mann–Wald theorem) или теорема о непрерывном отображении (англ. continuous mapping theorem, CMT) — положение теории вероятностей, которое утверждает, что непрерывные функции сохраняют предел даже в том случае, если их аргументы — последовательности случайных величин. Непрерывная функция в определении Гейне отображает сходящуюся последовательность в другую сходящуюся последовательность: если x_n → x, то g(x_n) → g(x). Теорема утверждает, что этот результат сохраняется и при замене детерминированной последовательности {x_n} на последовательность случайных величин {X_n}, а понятие сходимости для вещественных чисел — на один из типов сходимости случайных величин.

Теорема впервые доказана Манном и Вальдом в 1943 году^[1].

Формулировка

Пусть {X_n}, X — случайные элементы, определённые на метрическом пространстве S. Пусть функция g: S→S′ (где S′ есть другое метрическое пространство) разрывна в точках из множества D_g причём Pr[X ∈ D_g] = 0. Тогда^[2]^[3]^[4]

$X_{n}\ {\xrightarrow {d}}\ X\quad \Rightarrow \quad g(X_{n})\ {\xrightarrow {d}}\ g(X);$
$X_{n}\ {\xrightarrow {p}}\ X\quad \Rightarrow \quad g(X_{n})\ {\xrightarrow {p}}\ g(X);$
$X_{n}\ {\xrightarrow {\!\!as\!\!}}\ X\quad \Rightarrow \quad g(X_{n})\ {\xrightarrow {\!\!as\!\!}}\ g(X).$

См. также

Теорема Слуцкого

Примечания

↑ Amemiya, 1985, p. 88
↑ Van der Vaart, 1998, Theorem 2.3, page 7
↑ Billingsley, 1969, p. 31, Corollary 1
↑ Billingsley, 1999, p. 21, Theorem 2.7

Литература

Анатольев, Станислав. Эконометрика для продолжающих. Курс лекций (рус.). — Москва, 2006. — 60 с.
Amemiya, Takeshi. Advanced Econometrics (неопр.). — Cambridge, MA: Harvard University Press, 1985. — ISBN 0-674-00560-0.
Billingsley, Patrick^[англ.]. Convergence of Probability Measures (неопр.). — John Wiley & Sons, 1969. — ISBN 0-471-07242-7.
Billingsley, Patrick. Convergence of Probability Measures (неопр.). — 2nd. — John Wiley & Sons, 1999. — ISBN 0-471-19745-9.
Mann, H. B.; Wald, A.^[англ.]. On Stochastic Limit and Order Relationships (англ.) // Annals of Mathematical Statistics^[англ.] : journal. — 1943. — Vol. 14, no. 3. — P. 217—226. — doi:10.1214/aoms/1177731415. — JSTOR 2235800.
Van der Vaart, A. W. Asymptotic statistics (неопр.). — New York: Cambridge University Press, 1998. — ISBN 0-521-49603-9.

Похожие исследовательские статьи

Математи́ческое ожида́ние — понятие в теории вероятностей, означающее среднее значение случайной величины. В случае непрерывной случайной величины подразумевается взвешивание по плотности распределения. Математическое ожидание случайного вектора равно вектору, компоненты которого равны математическим ожиданиям компонентов случайного вектора.

Интегральный признак Коши́ — Макло́рена — признак сходимости убывающего положительного числового ряда. Признак Коши — Маклорена даёт возможность свести проверку сходимости ряда к проверке сходимости несобственного интеграла соответствующей функции на $\text{[math]}$ , последний часто может быть найден в явном виде.

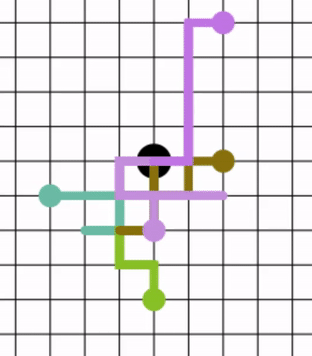
<span class="mw-page-title-main">Случайное блуждание</span>

Случайное блуждание — математический объект, известный как стохастический или случайный процесс, который описывает путь, состоящий из последовательности случайных шагов в каком-нибудь математическом пространстве.

Ле́мма Фату́ — техническое утверждение, используемое при доказательстве различных теорем в функциональном анализе и теории вероятностей. Оно даёт одно из условий, при которых предел почти всюду сходящейся функциональной последовательности будет суммируемым.

Центра́льные преде́льные теоре́мы (ЦПТ) — класс теорем в теории вероятностей, утверждающих, что сумма достаточно большого количества слабо зависимых случайных величин, имеющих примерно одинаковые масштабы, имеет распределение, близкое к нормальному.

Характеристи́ческая фу́нкция случа́йной величины́ — один из способов задания распределения. Характеристические функции могут быть удобнее в тех случаях, когда, например, плотность или функция распределения имеют очень сложный вид. Также характеристические функции являются удобным инструментом для изучения вопросов слабой сходимости. В теорию характеристических функций внесли большой вклад Ю. В. Линник, И. В. Островский, К. Р. Рао, Б. Рамачандран.

Последовательность функций сходится почти всюду к предельной функции, если множество точек, для которых сходимость отсутствует, имеет нулевую меру.

Теоре́ма Леви́ в теории вероятностей — результат, увязывающий поточечную сходимость характеристических функций случайных величин со сходимостью этих случайных величин по распределению.

Сходи́мость по ме́ре в функциональном анализе, теории вероятностей и смежных дисциплинах — это вид сходимости измеримых функций, заданных на пространстве с мерой.

Сходи́мость по распределе́нию в теории вероятностей — вид сходимости случайных величин.

В математике, поточечная сходимость последовательности функций на множестве — это вид сходимости, при котором каждой точке данного множества ставится в соответствие предел последовательности значений элементов последовательности в этой же точке.

<span class="mw-page-title-main">Закон больших чисел</span> математический принцип

Закон больших чисел (ЗБЧ) в теории вероятностей — принцип, описывающий результат выполнения одного и того же эксперимента много раз. Согласно закону, среднее значение конечной выборки из фиксированного распределения близко к математическому ожиданию этого распределения.

Теорема Вейерштра́сса — Стоуна — утверждение о возможности представления любой непрерывной функции на хаусдорфовом компакте пределом равномерно сходящейся последовательности непрерывных функций особого класса — алгебры Стоуна.

Степенной ряд с одной переменной — это формальное алгебраическое выражение вида:

\text{[math]}

Функциональный ряд — ряд, каждым членом которого, в отличие от числового ряда, является не число, а функция $\text{[math]}$ .

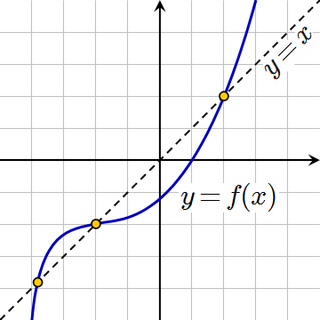
Неподвижная точка в математике — точка, которую заданное отображение переводит в неё же, иными словами, решение уравнения $\text{[math]}$ . Иногда такую точку называют инвариантной [по названию соответствующего у неё свойства].

ε-сеть для подмножества $\text{[math]}$ метрического пространства $\text{[math]}$ есть множество $\text{[math]}$ из того же пространства $\text{[math]}$ такое, что для любой точки $\text{[math]}$ найдётся точка $\text{[math]}$ , удалённая от $\text{[math]}$ не более чем на ε.

Линейный функционал $\text{[math]}$ называется банаховым пределом если выполняются следующие 3 условия:
1) $\text{[math]}$

Дельта-метод — вероятностное распределение функции от асимптотически нормальной статистической оценки при известной асимптотической дисперсии этой оценки.

Важнейшими с точки зрения приложений характеристических функций к выводу асимптотических формул теории вероятностей являются две предельные теоремы — прямая и обратная. Эти теоремы устанавливают, что соответствие, существующее между функциями распределения и характеристическими функциями, не только взаимно однозначно, но и непрерывно.

Эта страница основана на статье Википедии.
Текст доступен на условиях лицензии CC BY-SA 4.0; могут применяться дополнительные условия.
Изображения, видео и звуки доступны по их собственным лицензиям.