
Геоме́трия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения. В практических задачах геометрия позволяет предсказывать геометрические размеры тела, зная другие геометрические размеры этого тела с помощью известных геометрических законов.

Теорема Морли о трисектрисах — одна из теорем геометрии треугольника. Трисектрисами угла называются два луча, делящие угол на три равные части.
Здесь собраны определения терминов из планиметрии. Курсивом выделены ссылки на термины в этом словаре.
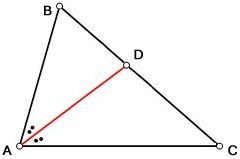
Биссектри́са угла — луч, исходящий из вершины угла и делящий этот угол на два равных угла. Можно также определить биссектрису как геометрическое место точек внутри угла, равноудалённых от сторон этого угла.
Геометри́ческое ме́сто то́чек (ГМТ) — математический термин, употребляется для определения геометрической фигуры как множества точек, обладающих некоторым свойством.

Построе́ния с по́мощью ци́ркуля и лине́йки — раздел евклидовой геометрии, известный с античных времён.
Трисекция угла — задача о делении заданного угла на три равные части построением циркулем и линейкой. Иначе говоря, необходимо построить трисектрисы угла — лучи, делящие угол на три равные части.

Правильный семиугольник — правильный многоугольник с семью сторонами.

Пра́вильный семнадцатиуго́льник — геометрическая фигура, принадлежащая к группе правильных многоугольников. Он имеет семнадцать сторон и семнадцать углов, все его углы и стороны равны между собой, все вершины лежат на одной окружности. Среди других правильных многоугольников с больши́м простым числом сторон интересен тем, что его можно построить при помощи циркуля и линейки.

Окружность Аполло́ния — геометрическое место точек плоскости, отношение расстояний от которых до двух заданных точек — величина постоянная, не равная единице.

Зада́ча Аполло́ния — построить с помощью циркуля и линейки окружность, касающуюся трёх данных окружностей.

Радика́льная ось — геометрическое место точек, степени которых относительно двух заданных окружностей равны. Иными словами, равны длины четырёх касательных, проведённых к двум данным окружностям из любой точки  данного геометрического места точек.
данного геометрического места точек.
Теорема Штейнера — Понселе — теорема из области геометрических построений, утверждающая, что любое построение, выполнимое на плоскости циркулем и линейкой, можно выполнить одной линейкой, если нарисована хотя бы одна окружность и отмечен её центр.
Квадрату́ра — математический термин, первоначально обозначавший нахождение площади какой-либо фигуры или поверхности. В дальнейшем смысл термина постепенно менялся. Задачи квадратуры послужили одним из главных источников возникновения в конце XVII века математического анализа.

Лоре́нцо Маскеро́ни — итальянский математик.

Задача Наполеона — знаменитая задача построения с помощью циркуля. В этой задаче дана окружность и её центр. Задача состоит в делении окружности на четыре равных дуги с помощью только циркуля. Наполеон был известным любителем математики, но неизвестно, он ли придумал или решил эту задачу. Друг Наполеона итальянский математик Лоренцо Маскерони придумал при геометрических построениях ограничение на использование только циркуля. Но, фактически, задача выше является более простой, чем истинная задача Наполеона, состоящая в нахождении центра окружности с помощью только циркуля. Ниже приведено решение обеих задач и даны доказательства.

Георг Мор — датский математик, первым доказавший теорему, известную как теорему Мора — Маскерони о построениях циркулем.

Не́всис — метод геометрического построения, цель которого — вписать отрезок заданной длины между двумя кривыми линиями таким образом, чтобы этот отрезок или его продолжение проходил через заданную точку.

Середина отрезка — точка на заданном отрезке, находящаяся на равном расстоянии от обоих концов данного отрезка. Является центром масс как всего отрезка, так и его конечных точек.
Геометрическая криптография — теоретические криптографические методы, в которых сообщения и шифротексты представлены в виде геометрических величин: углов, отрезков, а вычисления проводятся с помощью циркуля и линейки. Основана на сложности решения определенного класса геометрических задач, например, трисекции угла. Геометрическая криптография не имеет практического применения, но её предлагается использовать в педагогических целях, чтобы наглядно продемонстрировать принципы криптографии такие, как протокол с нулевым разглашением информации. Идея геометрической криптографии, а именно: идентификации с помощью трисекции угла, была предложена в неопубликованной работе в 1997 году. Является примером криптографии в нестандартной модели вычислений.














