
Преобразование Фурье́ — операция, сопоставляющая одной функции вещественной переменной другую функцию вещественной переменной. Эта новая функция описывает коэффициенты («амплитуды») при разложении исходной функции на элементарные составляющие — гармонические колебания с разными частотами.
В численном и функциональном анализе дискретные вейвлет-преобразования (ДВП) относятся к вейвлет-преобразованиям, в которых вейвлеты представлены дискретными сигналами (выборками).

Автокорреляционная функция (АКФ) — зависимость взаимосвязи между функцией (сигналом) и её сдвинутой по аргументу функции копией от величины сдвига.

Вейвлет-преобразование — интегральное преобразование, которое представляет собой свертку вейвлет-функции с сигналом. Вейвлет-преобразование переводит сигнал из временного представления в частотно-временное.
Пeрeда́точная фу́нкция — один из способов математического описания динамической системы. Используется в основном в теории управления, связи и цифровой обработке сигналов. Представляет собой дифференциальный оператор, выражающий связь между входом и выходом линейной стационарной системы. Зная входной сигнал системы и передаточную функцию, можно восстановить выходной сигнал.
Характеристи́ческая фу́нкция случа́йной величины́ — один из способов задания распределения. Характеристические функции могут быть удобнее в тех случаях, когда, например, плотность или функция распределения имеют очень сложный вид. Также характеристические функции являются удобным инструментом для изучения вопросов слабой сходимости. В теорию характеристических функций внесли большой вклад Ю. В. Линник, И. В. Островский, К. Р. Рао, Б. Рамачандран.
Преобразова́ние Лапла́са (ℒ) — интегральное преобразование, связывающее функцию  комплексного переменного (изображение) с функцией
комплексного переменного (изображение) с функцией  вещественного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения.
вещественного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения.
Дискретное преобразование Фурье — это одно из преобразований Фурье, широко применяемых в алгоритмах цифровой обработки сигналов, а также в других областях, связанных с анализом частот в дискретном сигнале.
Импульсная переходная функция — выходной сигнал динамической системы как реакция на входной сигнал в виде дельта-функции Дирака. В цифровых системах входной сигнал представляет собой простой импульс минимальной ширины и максимальной амплитуды. В применении к фильтрации сигнала называется также ядром фильтра. Находит широкое применение в теории управления, обработке сигналов и изображений, теории связи и других областях инженерного дела.
Теория линейных стационарных систем — раздел теории динамических систем, изучающий поведение и динамические свойства линейных стационарных систем (ЛСС). Используется для изучения процессов управления техническими системами, для цифровой обработки сигналов и в других областях науки и техники.
Спектра́льная пло́тность мо́щности (СПМ) — в физике и обработке сигналов — функция, описывающая распределение мощности сигнала по частотам, а именно мощность, приходящуюся на единичный интервал частоты. Имеет размерность мощности, делённой на частоту, то есть энергии. Например, в Международной системе единиц (СИ) это Вт/с−1 (Вт·с) или Вт/Гц, смотря по тому, какая частота используется:  (c-1) или
(c-1) или  (Гц). Общепринятого значка для СПМ нет, нередко используется символ
(Гц). Общепринятого значка для СПМ нет, нередко используется символ  . Единичный интервал по
. Единичный интервал по  в
в  раза шире, чем по
раза шире, чем по  , поэтому
, поэтому  .
.
Оконное преобразование Фурье — это разновидность преобразования Фурье, определяемая следующим образом:

Тригонометрический ряд Фурье — представление произвольной функции  с периодом
с периодом  в виде ряда
в виде ряда
Теорема Хинчина — Колмогорова утверждает, что спектральной плотностью мощности стационарного в широком смысле случайного процесса является преобразование Фурье соответствующей автокорреляционной функции.
Свёртка последовательностей — линейное преобразование двух числовых последовательностей. Результатом свёртки является последовательность, элементы которой получаются в результате перемножения и суммирования элементов исходных последовательностей таким образом, что члены одной последовательности берутся с возрастанием индексов, а члены другой — с убыванием. Различают линейную и циклическую свёртки, которые используются для конечных и периодических последовательностей соответственно.
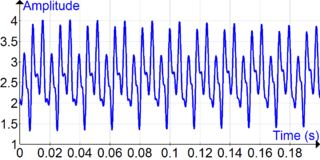
Анализ Фурье — направление в анализе, изучающее каким образом общие математические функции могут быть представлены либо приближены через сумму более простых тригонометрических функций. Анализ Фурье возник при изучении свойств рядов Фурье, и назван в честь Жозефа Фурье, который показал, что представление функции в виде суммы тригонометрических функций значительно упрощает изучение процесса теплообмена.
Преобразование Фурье на группах — обобщение дискретного преобразования Фурье от циклических к локально компактным абелевым группам или произвольным компактным группам.

В математике преобразование Вейерштрасса функции f : R → R, названное в честь Карла Вейерштрасса, представляет собой «сглаженную» версию f(x), полученную путём усреднения значений f, взвешенных с помощью гауссиана с центром в точке x.
Теорема о свёртке гласит, что при подходящих условиях преобразование Фурье свёртки двух функций является поточечным произведением их преобразований Фурье. В более общем случае свёртка в одной области равна точечному умножению в другой области. Другие версии теоремы о свёртке применимы к различным преобразованиям Фурье.





























