Фундамента́льная гру́ппа — одна из простейших конструкций в алгебраической топологии. Сопоставляется группа всякому связному топологическому пространству. Для подмножеств плоскости эта группа измеряет количество «дырок». Наличие «дырки» определяется невозможностью непрерывно продеформировать (стянуть) некоторую замкнутую кривую в точку.
Мо́щность, или кардина́льное число́, мно́жества — характеристика множеств, обобщающая понятие количества (числа) элементов конечного множества.

Гамма-функция — математическая функция. Была введена Леонардом Эйлером, а своим обозначением гамма-функция обязана Лежандру.
Кривизна́ — собирательное название ряда характеристик, описывающих отклонение того или иного геометрического «объекта» от соответствующих «плоских» объектов.

Теорема Гаусса — один из основных законов электродинамики, входит в систему уравнений Максвелла. Выражает связь между потоком напряжённости электрического поля сквозь замкнутую поверхность произвольной формы и алгебраической суммой зарядов, расположенных внутри объёма, ограниченного этой поверхностью. Применяется отдельно для вычисления электростатических полей.
Локально тривиальное расслоение — расслоение, которое локально выглядит как прямое произведение.
Зонная структура графена рассчитана в 1947 году в статье. На внешней оболочке атома углерода находится 4 электрона, три из которых образуют sp² гибридизированные связи с соседними атомами в решётке, а оставшийся электрон находится в 2pz состоянии. В нашем рассмотрении он отвечает за образование энергетических зон графена.
Изопериметри́ческое нера́венство — геометрическое неравенство, связывающее периметр замкнутой кривой на плоскости и площадь участка плоскости, ограниченной этой кривой. Этот термин также используется для различных обобщений данного неравенства.
Уравнение Фридмана — в космологии уравнение, описывающее развитие во времени однородной и изотропной Вселенной в рамках общей теории относительности. Названо по имени Александра Александровича Фридмана, который первым вывел это уравнение в 1922 году.
Теория Эйнштейна — Картана (ЭК) была разработана как расширение общей теории относительности, внутренне включающее в себя описание воздействия на пространство-время кроме энергии-импульса также и спина материальных полей. В теории ЭК вводится аффинное кручение, а вместо псевдоримановой геометрии для пространства-времени используется геометрия Римана — Картана. В результате от метрической теории переходят к аффинной теории пространства-времени. Результирующие уравнения для описания пространства-времени распадаются на два класса. Один из них аналогичен общей теории относительности, с тем отличием, что в тензор кривизны включены компоненты с аффинным кручением. Второй класс уравнений задаёт связь тензора кручения и тензора спина материи и излучения. Получаемые поправки к общей теории относительности в условиях современной Вселенной настолько малы, что пока не видно даже гипотетических путей для их измерения.
Пропагатор в квантовой механике и квантовой теории поля (КТП) — функция, характеризующая распространение релятивистского поля от одного акта взаимодействия до другого. Эта функция определяет амплитуду вероятности перемещения частицы из одного места пространства в другое за заданный промежуток времени или перемещения частицы с определённой энергией и импульсом. Для расчёта частоты столкновений в КТП используются виртуальные частицы, представленные в диаграммах Фейнмана пропагаторами, вносят свой вклад в вероятность рассеяния, описываемого соответствующей диаграммой. Их также можно рассматривать как оператор, обратный волновому оператору, соответствующему частице, и поэтому их часто называют (причинными) функциями Грина.

В функциональном анализе и связанных областях математики стереотипные пространства представляют собой класс топологических векторных пространств, выделяемый неким специальным условием рефлексивности. Этот класс обладает серией замечательных свойств, в частности, он весьма широк, он состоит из пространств, подчиненных определенному условию полноты, и образует замкнутую моноидальную категорию со стандартными аналитическими средствами построения новых пространств, такими как переход к замкнутому подпространству, факторпространству, проективному и инъективному пределам, пространству операторов, тензорным произведениям, и т. д.
Физические свойства графена проистекают из электронных свойств атомов углерода и поэтому часто имеют нечто общее с остальными аллотропными модификациями углерода, которые были известны до него, такими как графит, алмаз, углеродные нанотрубки. Конечно, схожести больше с графитом, так как он состоит из графеновых слоёв, но без новых уникальных физических явлений и исследований других материалов и наработок физических методов анализа и теоретических подходов графен не привлёк бы специалистов из таких разных дисциплин как физика, химия, биология и физика элементарных частиц.
Теорема сравнения Топоногова — классическая теорема римановой геометрии в целом.
Переход Костерлица — Таулеса или переход Березинского — Костерлица — Таулеса (БКТ-переход) или топологический фазовый переход — фазовый переход в двумерной XY-модели. Это переход из состояния связанных пар вихрь-антивихрь при низких температурах в состояние с неспаренными вихрями и антивихрями при некоторой критической температуре. Переход назван в честь занимающихся конденсированными средами физиков Вадима Львовича Березинского, Джона М. Костерлица и Дэвида Дж. Таулеса. БКТ-переходы можно наблюдать в некоторых двумерных системах в физике конденсированных сред, которые аппроксимируются с помощью XY-модели, в том числе в массиве джозефсоновских контактов и в тонких сверхпроводящих гранулированных плёнках. Этот термин также используется как название пиннинга куперовских пар в изолирующем режиме из-за сходства с обычным вихревым БКТ-переходом.
Формула Крофтона — классический результат интегральной геометрии. Связывает длину кривой со средним числом пересечений с прямыми.

Формула Эйлера — формула, позволяющая вычислить нормальную кривизну поверхности.
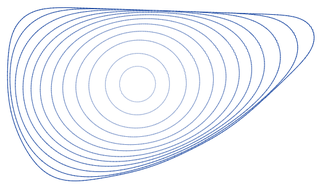
Укорачивающий поток — процесс, изменяющий гладкую кривую на плоскости путём перемещения её точек перпендикулярно к кривой со скоростью, равной её кривизне.

Вариация поворота кривой — интеграл кривизны кривой по её длине.


















