Теорема Стоуна о группах унитарных операторов в гильбертовом пространстве

Теорема Стоуна о группах унитарных операторов в гильбертовом пространстве — важный результат функционального анализа, утверждающий, что всякая сильно непрерывная однопараметрическая группа унитарных операторов представляется в виде:

U_{t}=e^{it{\hat {H}}}\quad t\in \mathbb {R}

где ${\hat {H}}$ — некоторый самосопряженный оператор, а $t$ — параметр. Верно и обратное: всякому самосопряженному оператору ${\hat {H}}$ с помощью представления Стоуна можно поставить в соответствие сильно непрерывную однопараметрическую группу унитарных операторов.

Теорема была доказана американским математиком Маршаллом Стоуном в 1930 году и имела большое значение для становления квантовой механики, а также послужила толчком к созданию теории Купмана — фон Неймана.

Сильно непрерывная однопараметрическая группа унитарных операторов обладает следующими свойствами:

\lim _{t\rightarrow t_{0}}U_{t}\xi =U_{t_{0}}\xi \quad \forall t_{0}\in \mathbb {R} ,\xi \in H

U_{t+s}=U_{t}U_{s}

Важность результата для физики заключается в том, что он гарантирует существование и единственность решений уравнений Шрёдингера и Лиувилля, а также сохранение нормировок волновых функций.

Ссылки

Stone, M. H. (1930), "Linear Transformations in Hilbert Space. III. Operational Methods and Group Theory", Proceedings of the National Academy of Sciences of the United States of America, 16 (2), National Academy of Sciences: 172—175, ISSN 0027-8424
Stone, M. H. (1932), "On one-parameter unitary groups in Hilbert Space", Annals of Mathematics, 33 (3): 643—648
K. Yosida, Functional Analysis, Springer-Verlag, (1968).

Похожие исследовательские статьи

Кватернио́ны — система гиперкомплексных чисел, образующая векторное пространство размерностью четыре над полем вещественных чисел. Обычно обозначаются символом $\text{[math]}$ . Предложены Уильямом Гамильтоном в 1843 году.

Непрерывная функция — функция, которая меняется без мгновенных «скачков», то есть такая, малые изменения аргумента которой приводят к малым изменениям значения функции.

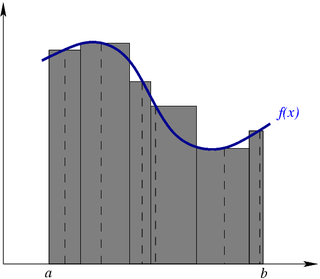
<span class="mw-page-title-main">Интеграл Римана</span> простейшее определение интеграла

Интегра́л Ри́мана — наиболее широко используемый вид определённого интеграла. Очень часто под термином «определённый интеграл» понимается именно интеграл Римана, и он изучается самым первым из всех определённых интегралов во всех курсах математического анализа. Введён Бернхардом Риманом в 1854 году, и является одной из первых формализаций понятия интеграла.

Разностная схема — это конечная система алгебраических уравнений, поставленная в соответствие какой-либо дифференциальной задаче, содержащей дифференциальное уравнение и дополнительные условия. Таким образом, разностные схемы применяются для сведения дифференциальной задачи, имеющей континуальный характер, к конечной системе уравнений, численное решение которых принципиально возможно на вычислительных машинах. Алгебраические уравнения, поставленные в соответствие дифференциальному уравнению, получаются применением разностного метода, что отличает теорию разностных схем от других численных методов решения дифференциальных задач.

Краевая задача — задача о нахождении решения заданного дифференциального уравнения, удовлетворяющего краевым (граничным) условиям в концах интервала или на границе области. Краевые задачи для гиперболических и параболических уравнений часто называют начально-краевыми или смешанными, потому что в них задаются не только граничные, но и начальные условия.

В математике оператор $\text{[math]}$ в комплексном или действительном гильбертовом пространстве $\text{[math]}$ называется эрмитовым, симметрическим, если он удовлетворяет равенству $\text{[math]}$ для всех $\text{[math]}$ из области определения $\text{[math]}$ . Здесь и далее полагается, что $\text{[math]}$ — скалярное произведение в $\text{[math]}$ . Название дано в честь французского математика Шарля Эрмита.

Унитарный оператор — ограниченный линейный оператор $\text{[math]}$ на гильбертовом пространстве $\text{[math]}$ , который удовлетворяет соотношению:

\text{[math]}

Предел вдоль фильтра — обобщение понятия предела.

<span class="mw-page-title-main">Теорема Тейлора</span>

Теорема Тейлора даёт приближение к функции, дифференцируемой k раз, вблизи данной точки с помощью многочлена Тейлора k-го порядка. Для аналитических функций многочлен Тейлора в данной точке является частичной суммой их ряда Тейлора, который, в свою очередь, полностью определяет функцию в некоторой окрестности точки. Точное содержание теоремы Тейлора до настоящего времени не согласовано. Конечно, существует несколько версий теоремы, применимых в различных ситуациях, и некоторые из этих версий содержат оценки ошибки, возникающей при приближении функции с помощью многочлена Тейлора.

Четвёртая проблема Гильберта в списке проблем Гильберта касается базовой системы аксиом геометрии. Проблема состоит в том, чтобы

«Определить все с точностью до изоморфизма реализации систем аксиом классических геометрий, если в них опустить аксиомы конгруэнтности, содержащие понятия угла, и пополнить эти системы аксиомой неравенства треугольника».

Теорией Ку́пмана — фон Не́ймана (KvN-теорией) в математической физике называется оригинальная переформулировка классической статистической механики, созданная американскими математиками Джоном фон Нейманом и Бернардом Купманом. Формализм механики Купмана — фон Неймана максимально приближен к формализму нерелятивистской квантовой механики: состояние динамической системы в ней описывается при помощи классической волновой функции, являющейся аналогом квантовомеханической волновой функции, классическое уравнение Лиувилля приобретает математическую структуру уравнения Шрёдингера и т. д.

Нормальный оператор — линейный ограниченный оператор в гильбертовом пространстве, перестановочный со своим сопряжённым: $\text{[math]}$ . Частными случаями нормальных операторов являются самосопряжённые операторы: $\text{[math]}$ и унитарные операторы: $\text{[math]}$ . Для нормальных операторов выполняется спектральная теорема.

Группа Лоренца является группой Ли симметрий пространства-времени в специальной теории относительности. Эта группа может быть реализована как набор матриц, линейных преобразований или унитарных операторов на некотором гильбертовом пространстве. Группа имеет различные представления. В любой релятивистски инвариантной физической теории эти представления как-то должны быть отражены. Сама физика должна быть сделана на их основе. Более того, специальная теория относительности вместе с квантовой механикой являются двумя физическими теориями, которые тщательно проверены и объединение этих двух теорий сводится к изучению бесконечномерных унитарных представлений группы Лоренца. Это имеет как историческую важность в основном течении в теоретической физике, так и связи с более спекулятивными теориями настоящего времени.

Унитарность в квантовой физике — условие, что временная эволюция квантового состояния в соответствии с уравнением Шрёдингера математически представлена унитарным оператором. Это обычно принимается как аксиома или основной постулат квантовой механики, в то время как обобщения или отклонения от унитарности являются частью предположений в теориях, которые могут выходить за рамки квантовой механики. Граница унитарности — это любое неравенство, которое следует из унитарности оператора эволюции, то есть из утверждения, что эволюция во времени сохраняет внутренние произведения в гильбертовом пространстве.

Представление группы Ли — это линейное действие группы Ли на векторном пространстве или, что то же самое, гладкий гомоморфизм группы Ли в группу обратимых операторов на векторном пространстве. Играет важную роль в изучении непрерывной симметрии в математике и теоретической физике. Представления групп Ли изучены довольно хорошо, основным инструментом их изучения является использование соответствующих «инфинитезимальных» представлений алгебр Ли.

Симметрии в квантовой механике — преобразования пространства-времени и частиц, которые оставляют неизменными уравнения квантовой механики. Рассматриваются во многих разделах квантовой механики, которые включают релятивистскую квантовую механику, квантовую теорию поля, стандартную модель и физику конденсированного состояния. В целом, симметрия в физике, законы инвариантности и сохранения являются основополагающими ограничениями для формулирования физических теорий и моделей. На практике это мощные методы решения задач и прогнозирования того, что может случиться. Хотя законы сохранения не всегда дают конечное решение проблемы, но они формируют правильные ограничения и наметки к решению множества задач.

Групповой анализ дифференциальных уравнений — раздел математики, изучающий свойства симметрии дифференциальных уравнений относительно различных преобразований зависимых и независимых переменных. Включает в себя методы и прикладные аспекты дифференциальной геометрии, теории групп и алгебр Ли, вариационного исчисления и является, в свою очередь, эффективным инструментом исследования в теории ОДУ, ДУЧП и математической физике.

Тождество Похожаева — это интегральное соотношение, которому удовлетворяют стационарные локализованные решения нелинейного уравнения Шредингера или нелинейного уравнения Клейна-Гордона. Оно было получено С.И. Похожаевым и аналогично теореме о вириале. Это соотношение также известно как теорема Д.Г. Деррика. Аналогичные тождества могут быть получены и для других уравнений математической физики.

Спектральная мера - это отображение, определённое на $\text{[math]}$ -алгебре подмножеств заданного множества, значения которого являются ортогональными проекторами в гильбертовом пространстве.

Псевдодифференциальный оператор — расширение концепции дифференциального оператора в математическом анализе. Псевдодифференциальные операторы широко применяются в теории уравнений в частных производных и квантовой теории поля, например, в математических моделях, которые включают ультраметрические псевдодифференциальные уравнения в неархимедовом пространстве.

Эта страница основана на статье Википедии.
Текст доступен на условиях лицензии CC BY-SA 4.0; могут применяться дополнительные условия.
Изображения, видео и звуки доступны по их собственным лицензиям.