Измери́мые функции представляют естественный класс функций, связывающих пространства с выделенными алгебрами множеств, в частности измеримыми пространствами.
Непрерывная функция — функция, которая меняется без мгновенных «скачков», то есть такая, малые изменения аргумента которой приводят к малым изменениям значения функции.
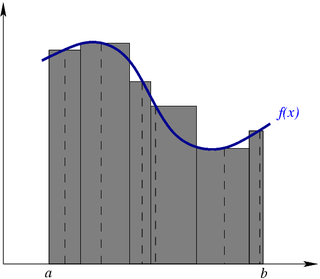
Интегра́л Ри́мана — наиболее широко используемый вид определённого интеграла. Очень часто под термином «определённый интеграл» понимается именно интеграл Римана, и он изучается самым первым из всех определённых интегралов во всех курсах математического анализа. Введён Бернхардом Риманом в 1854 году, и является одной из первых формализаций понятия интеграла.
Мера Жордана — один из способов формализации понятия длины, площади и  -мерного объёма в
-мерного объёма в  -мерном евклидовом пространстве.
-мерном евклидовом пространстве.
Распределение вероятностей — это закон, описывающий область значений случайной величины и вероятности их исхода (появления).

Голоморфная функция, иногда называемая регулярной функцией — функция комплексного переменного, определённая на открытом подмножестве комплексной плоскости  и комплексно дифференцируемая в каждой точке.
и комплексно дифференцируемая в каждой точке.
Ме́ра Лебе́га на  — мера, обобщающая понятия длины отрезка, площади фигуры и объёма тела на произвольное
— мера, обобщающая понятия длины отрезка, площади фигуры и объёма тела на произвольное  -мерное евклидово пространство. Говоря более формально, мера Лебега является продолжением меры Жордана на более широкий класс множеств.
-мерное евклидово пространство. Говоря более формально, мера Лебега является продолжением меры Жордана на более широкий класс множеств.

Интеграл Лебе́га — это обобщение интеграла Римана на более широкий класс функций.
Теоре́ма Лебе́га о мажори́руемой сходи́мости в функциональном анализе, теории вероятностей и смежных дисциплинах — это теорема, утверждающая, что если сходящаяся почти всюду последовательность измеримых функций может быть ограничена по модулю сверху интегрируемой функцией, то все члены последовательности, а также предельная функция тоже интегрируемы. Более того, интеграл последовательности сходится к интегралу её предела.
Ле́мма Фату́ — техническое утверждение, используемое при доказательстве различных теорем в функциональном анализе и теории вероятностей. Оно даёт одно из условий, при которых предел почти всюду сходящейся функциональной последовательности будет суммируемым.
Теоре́ма Его́рова утверждает, что последовательность измеримых функций, сходящаяся почти всюду на некотором множестве, сходится равномерно на достаточно большом его подмножестве.
Пло́тность вероя́тности — один из способов задания распределения случайной величины. Во многих практических приложениях понятия «плотность вероятности» и «плотность (распределения) случайной величины» или «функция распределения вероятностей» фактически синонимизируются и под ними подразумевается вещественная функция, характеризующая сравнительную вероятность реализации тех или иных значений случайной переменной (переменных).
Теоре́ма Радо́на — Нико́дима в функциональном анализе и смежных дисциплинах описывает общий вид меры, абсолютно непрерывной относительно другой меры.
Примечание: всюду в данной статье, где используется знак  имеется в виду (кратный) интеграл Римана
имеется в виду (кратный) интеграл Римана  , если не оговорено обратное;
, если не оговорено обратное;
всюду в данной статье, где говорится об измеримости множества, имеется в виду измеримость по Жордану, если не оговорено обратное.
Предел вдоль фильтра — обобщение понятия предела.
Теорема Дирихле о единицах — теорема алгебраической теории чисел, описывающая ранг подгруппы обратимых элементов кольца алгебраических целых  числового поля
числового поля  .
.

В математическом анализе множество меры 0, также известное как «множество с нулевым содержимым» — измеримое по Лебегу множество действительных чисел, имеющее меру ноль. Его можно охарактеризовать как множество, которое можно покрыть счётным объединением интервалов произвольно малой общей длины.





































