Четырёхугольник — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин), никакие три из которых не лежат на одной прямой, и четырёх отрезков (сторон), последовательно соединяющих эти точки. Различают выпуклые и невыпуклые четырёхугольники, невыпуклый четырёхугольник может быть самопересекающимся. Четырёхугольник без самопересечений называется простым, часто под термином «четырёхугольник» имеются в виду только простые четырёхугольники.

Окружность девяти точек — это окружность, проходящая через середины всех трёх сторон треугольника.

Теорема Фейербаха — результат геометрии треугольника. Теорема была сформулирована и доказана Карлом Вильгельмом Фейербахом в 1822 году.
Здесь собраны определения терминов из планиметрии. Курсивом выделены ссылки на термины в этом словаре.

Вневпи́санная окружность треугольника — окружность, касающаяся одной из сторон треугольника и продолжений двух других его сторон. У любого треугольника существует три вневписанных окружности.

Центр вписанной окружности треугольника (инцентр) — одна из замечательных точек треугольника, точка пересечения биссектрис треугольника. Центр вписанной в треугольник окружности также иногда называют инцентром.

Папп Александри́йский — математик и механик эпохи позднего эллинизма, живший и работавший в Александрии.

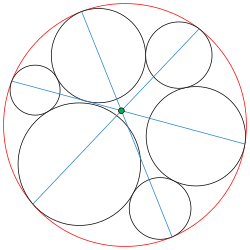
Поризм Понселе — классическая теорема проективной геометрии. Назван в честь Жан-Виктора Понселе.

Формула Эйлера — теорема планиметрии, связывает расстояние между центрами вписанной и описанной окружностей и их радиусами.

Вписанная в треугольник окружность — окружность внутри треугольника, касающаяся всех его сторон; наибольшая окружность, которая может находиться внутри треугольника. Центр этой окружности является точкой пересечения биссектрис треугольника и называется инцентром треугольника.

Теорема Кейси или Кэзи — теорема в евклидовой геометрии, обобщающая неравенство Птолемея. Названа по имени ирландского математика Джона Кейси.

Набор окружностей Джонсона состоит из трёх окружностей одинакового радиуса r, имеющих одну общую точку пересечения H. В такой конфигурации окружности обычно имеют четыре точки пересечения — это общая точка пересечения H, через которую проходят все три окружности, и по дополнительной точке для каждой пары окружностей. Если любые две окружности не пересекаются они имеют лишь одну общую точку — H, и в этом случае считается, что H является и их попарной точкой пересечения также. Если же окружности совпадают, принимается за попарную точку пересечения точка, диаметрально противоположная точке H. Три точки попарных пересечений окружностей Джонсона образуют опорный треугольник Δ ABC фигуры. Конфигурация названа именем Роджера Артура Джонсона.

Теорема Лестера — утверждение в геометрии треугольника, согласно которому в любом разностороннем треугольнике две точки Ферма, центр девяти точек и центр описанной окружности лежат на одной окружности. Названа именем канадского математика Джун Лестер.

Теорема Микеля — утверждение в планиметрии, связанное с пересечением трёх окружностей, построенных вокруг вершин треугольника. Названа в честь французского математика Огюста Микеля. Эта теорема — один из нескольких результатов, касающийся окружностей в геометрии, полученный Микеле и опубликованных им в Journal de mathématiques pures et appliquées.

Цепь Паппа Александри́йского — кольцо внутри двух касающихся кругов, заполненных попарно касающимися кругами меньших диаметров. Исследована Паппом Александрийским в III веке н. э.

Теорема Косниты — это свойство некоторых окружностей, связанных с произвольным треугольником.

Теорема о пяти окружностях утверждает: пусть дана цепочка из пяти окружностей, и каждые две соседние из них пересекаются; также дана шестая окружность, которой принадлежат центры пяти окружностей и одна из точек пересечения каждой пары соседних окружностей ; тогда прямые, соединяющие точки пересечения, ближайшие к центру этой шестой окружности, образуют пентаграмму, вершины которой лежат на этих пяти окружностях.

Теоремы Клиффорда, названные именем английского геометра Уильяма Кингдона Клиффорда, — это последовательность теорем о пересечении окружностей.

Точка Фейербаха — точка касания вписанной окружности к окружности девяти точек треугольника. Точка Фейербаха является касательной точкой треугольника, что означает то, что её определение не зависит от расположения и размеров треугольника. Точка внесена с кодом X(11) в энциклопедию центров треугольника Кларка Кимберлинга и названа именем Карла Вильгельма Фейербаха.

Ортополюс системы, состоящей из треугольника ABC и прямой линии ℓ в данной плоскости, является точкой, определяемой следующим образом.. Пусть A ′, B ′, C ′ — основания перпендикуляров, проведенных к прямой ℓ из вершин треугольника соответственно A, B, C. Пусть A ′′, B ′′, C ′′ — основания перпендикуляров, проведенных к соответствующим противоположным сторонам A, B, C указанного треугольника или к продолжениям этих сторон. Тогда три прямые линии A ′ A ′′, B ′ B ′′, C ′ C ′′, пересекутся в одной точке — в ортополюсе H. Благодаря своим многочисленным свойствам ортополюсы стали предметом серьезного изучения . Изучались некоторые ключевые понятия — определение линий, имеющих данный ортополюс и ортополюсные окружности.