
Тео́рия упру́гости — раздел механики сплошных сред, изучающий деформации упругих твёрдых тел, их поведение при статических и динамических нагрузках.

Те́нзор — применяемый в математике и физике математический объект линейной алгебры, заданный на векторном пространстве конечной размерности. В физике в качестве векторного пространства обычно выступает физическое трёхмерное пространство или четырёхмерное пространство-время, а компонентами тензора являются координаты (проекции) взаимосвязанных физических величин. Использование тензоров в физике позволяет глубже понять физические законы и уравнения, упростить их запись за счёт сведения многих связанных физических величин в один тензор, а также записывать уравнения в форме, не зависящей от выбранной системы отсчёта.

Симметрическая группа — группа всех перестановок заданного множества  относительно операции композиции.
относительно операции композиции.

Корреля́ция, или корреляцио́нная зави́симость — статистическая взаимосвязь двух или более случайных величин, при этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин.

Векторное произведение двух векторов в трёхмерном евклидовом пространстве — вектор, перпендикулярный обоим исходным векторам, длина которого численно равна площади параллелограмма, образованного исходными векторами, а выбор из двух направлений определяется так, чтобы тройка из по порядку стоящих в произведении векторов и получившегося вектора была правой. Векторное произведение коллинеарных векторов считается равным нулевому вектору.

Теоре́ма Нётер или первая теорема Нётер утверждает, что каждой дифференцируемой симметрии действия для физической системы с консервативными силами соответствует закон сохранения. Теорема была доказана математиком Эмми Нётер в 1915 году и опубликована в 1918 году. Действие для физической системы представляет собой интеграл по времени функции Лагранжа, из которого можно определить поведение системы согласно принципу наименьшего действия. Эта теорема применима только к непрерывным и гладким симметриям над физическим пространством.

Цикло́ида — плоская трансцендентная кривая.

Электропрово́дность — способность тела (среды) проводить электрический ток, свойство тела или среды, определяющее возникновение в них электрического тока под воздействием электрического поля. Также физическая величина, характеризующая эту способность и обратная электрическому сопротивлению.

Соприкаса́ющаяся окру́жность, окру́жность кривизны́ — окружность, являющаяся наилучшим приближением заданной кривой в окрестности данной точки. В этой точке кривая и означенная окружность имеют касание, порядок которого не ниже 2. Окружность кривизны существует в каждой точке дважды дифференцируемой кривой с отличной от нуля кривизной; в случае нулевой кривизны в качестве соприкасающейся надлежит рассматривать касательную прямую — «окружность бесконечного радиуса».
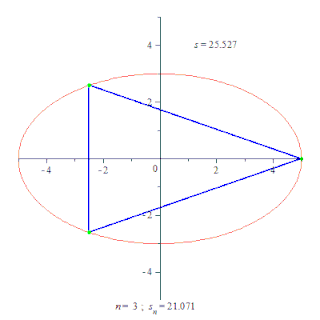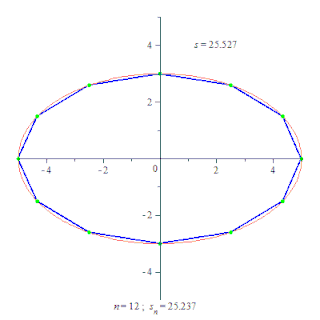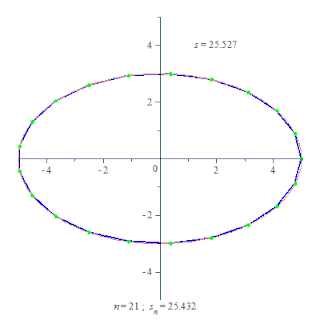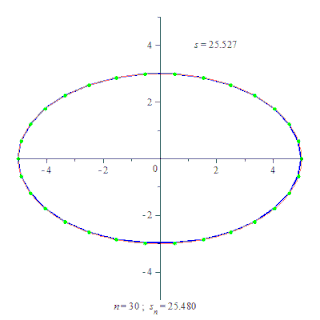
Длина́ криво́й — числовая характеристика протяжённости этой кривой. Исторически вычисление длины кривой называлось спрямлением кривой.

В механике сплошной среды механическое напряжение — это физическая величина, которая выражает внутренние силы, которые соседние частицы в непрерывной среде оказывают друг на друга, а деформация — это мера изменения геометрических размеров среды. Например, когда сплошная вертикальная штанга поддерживает груз, каждая частица в штанге давит на частицы, находящиеся непосредственно под ней. Когда жидкость находится в закрытом контейнере под давлением, каждая частица сталкивается со всеми окружающими частицами. Стенки контейнера и поверхность, создающая давление, прижимаются к ним в соответствии с силой реакции. Эти макроскопические силы на самом деле являются чистым результатом очень большого количества межмолекулярных сил и столкновений между частицами в этих средах. Механическое напряжение или в дальнейшем напряжение часто обозначается строчной греческой буквой сигма σ.
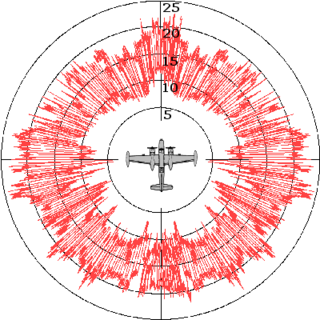
Эффекти́вная пло́щадь рассе́яния в радиолокации — площадь некоторой фиктивной плоской поверхности, расположенной нормально к направлению падающей плоской волны и являющейся идеальным и изотропным переизлучателем, которая, будучи помещена в точку расположения цели, создаёт в месте расположения антенны радиолокационной станции ту же плотность потока мощности, что и реальная цель.
Конъюнкти́вный одночле́н — булева формула, представляющая собой конъюнкцию литералов:
 ,
,
Гиперповерхность является обобщением понятия поверхности 3-мерного пространства для n-мерного пространства; это многообразие размерности n, которое вложено в евклидово пространство на единицу большей размерности  .
.
Символическая динамика — объединяющее название класса динамических систем, для которых точками фазового пространства являются последовательности в некотором конечном алфавите «символов», а отображение заключается в сдвиге последовательности на один символ влево.
Четвёртая проблема Гильберта в списке проблем Гильберта касается базовой системы аксиом геометрии. Проблема состоит в том, чтобы
«Определить все с точностью до изоморфизма реализации систем аксиом классических геометрий, если в них опустить аксиомы конгруэнтности, содержащие понятия угла, и пополнить эти системы аксиомой неравенства треугольника».
Физические свойства графена проистекают из электронных свойств атомов углерода и поэтому часто имеют нечто общее с остальными аллотропными модификациями углерода, которые были известны до него, такими как графит, алмаз, углеродные нанотрубки. Конечно, схожести больше с графитом, так как он состоит из графеновых слоёв, но без новых уникальных физических явлений и исследований других материалов и наработок физических методов анализа и теоретических подходов графен не привлёк бы специалистов из таких разных дисциплин как физика, химия, биология и физика элементарных частиц.
Вложение Сегре используется в проективной геометрии для того, чтобы рассматривать прямое произведение двух проективных пространств как проективное многообразие. Названо в честь итальянского математика Беньямино Сегре.


























