Техническая термодинамика

Техни́ческая термодина́мика — раздел теплотехники и одновременно раздел термодинамики, занимающийся приложениями законов термодинамики в теплоэнергетике, теплотехнике и хладотехнике^[1]. Исторически термодинамика начала формироваться именно как техническая термодинамика — учение о превращении теплоты в работу. На этой стадии были сформулированы основные законы классической термодинамики и получены их математические выражения. В дальнейшем область термодинамических исследований расширяется и охватывает различные области физики, химии, биологии, космологии и т. д. В настоящее время термодинамику можно определить как общую феноменологическую науку об энергии, исследующую разнообразные явления природы с позиции основных законов (начал) термодинамики. Специальные приложения термодинамики носят соответствующие названия физической, химической, технической, релятивистской и т. п. термодинамики.

Классическая термодинамика — пример аксиоматической науки^[2]. Принятый в ней дедуктивный метод исследований заключается в строгом математическом развитии некоторых исходных положений — физических постулатов, являющихся обобщением многовекового опыта познания природы. Термодинамика — помимо своих постулатов — не использует никаких гипотез, то есть предположений, требующих последующей опытной проверки. В частности, термодинамика не использует никаких гипотез и теорий строения вещества. Гипотезы о дискретном строении вещества используются в молекулярно-кинетической теории и статистической физике. В термодинамике такого рода представления могут быть использованы лишь в качестве иллюстративных средств. Отказ от использования гипотез в термодинамике ограничивает возможности её развития, однако, ценой этого ограничения достигается уверенность в надёжности расчётных соотношений термодинамики, эквивалентная уверенности в надёжности её исходных постулатов^[3].

В технической термодинамике рассматривают:

• технические приложения основных принципов термодинамики к процессам преобразования теплоты в работу или, наоборот, работы в теплоту в тепловых машинах — двигателях, турбинах, компрессорах, холодильниках и т. д.; рассматриваются теоретические основы работы тепловых машин и оценки эффективности их рабочих процессов^[4].
• методы прямого преобразования теплоты в электрическую энергию;
• процессы теплообмена (теплопроводности, лучистого переноса и др.);
• теплотехнические свойства веществ^[1].

Главной задачей, которая стояла перед учёными и инженерами в XIX и начале XX века было создание теории работы тепловых машин, которая позволила бы поставить на научную основу расчёт и проектирование поршневых паровых машин, паровых турбин, двигателей внутреннего сгорания, холодильных машин и т. д.

Основу термодинамики как новой науки заложил Сади Карно в опубликованном в 1824 г. трактате «Размышления о движущей силе огня и о машинах, способных развивать эту силу». В своей работе Карно придерживался господствующей в то время теплородной теории, согласно которой теплота представляла собой некоторую субстанцию (флюид) под названием теплород, способный впитываться телами в зависимости от их массы и температурных условий, и его количество во всех процессах остаётся неизменным. Получение работы в тепловой машине, согласно теплородной теории, объяснялось падением теплорода с более высокого температурного уровня на более низкий, аналогично принципу работы водяных турбин. Основным содержанием работы Карно являлось исследование условий наивыгоднейшей работы тепловых двигателей при наличии двух источников постоянных температур ${\displaystyle t_{1}}$ и ${\displaystyle t_{2}}$. В рассуждениях, содержащих решение этой задачи, Карно развивает идею о круговых процессах (циклах), разрабатывает схему цикла, носящего его имя, вводит понятие об обратимых процессах и в конечном счёте приходит к такому выводу: «Движущая сила тепла не зависит от агентов (рабочих тел), взятых для её развития; её количество исключительно определяется температурами тел, между которыми, в конечном счёте, производится перенос теплорода». При доказательстве этого утверждения Карно использовал два взаимно исключающих принципа: теорию теплорода и гидравлическую аналогию, противоречащие закону сохранения энергии, и принципу исключённого Perpetuum mobile I рода для механических явлений, который находится в полном соответствии с законом сохранения энергии и является его частным выражением. С современной точки зрения конечный вывод Карно о независимости коэффициента полезного действия тепловых двигателей от природы рабочего вещества и об определяющей роли температур внешних источников в процессах обратимых тепловых двигателей не может считаться обоснованным, однако, вывод этот верен^[5].

В середине XIX века, вскоре после опубликования работы Карно представления о теплороде были окончательно оставлены. Сокрушительный удар по теплородной теории был нанесён ещё в конце XVIII века опытами Румфорда и Дэви, но большинство физиков в течение полувека не желало отказаться от теории теплорода. Несмотря на всю свою наивность, эта теория так просто и наглядно объясняла многие явления, что даже будучи полностью ниспровергнутой, продолжала очень долго владеть умами учёных. Нагревание тел при трении теплородная теория объясняла перенесением теплорода из окружающей среды с более низким температурным уровнем к телам с более высоким температурным уровнем за счёт затрачиваемой работы. Румфорд в 1798 г., наблюдая за процессом сверления пушечных стволов, заметил, что во время совершения этой работы, которой сопутствует трение, непрерывно выделяется огромное количество тепла, и при этом никакого охлаждения окружающей среды (воздуха) не происходит. В 1799 г. Г. Дэви провёл опыт по трению между охлаждёнными ниже температуры плавления двумя кусками льда в безвоздушном пространстве, защищённом от солнечного и теплового излучения. При этом наблюдалось плавление льда, требующее больших затрат тепла. Таким образом было доказано, что выделение тепла при трении происходит не за счёт заимствования его из окружающей среды, как ошибочно объясняла теплородная теория, а за счёт затраченной работы^[6]. По-видимому, около 1830 г. Сади Карно отказался от теплородной теории и впервые отчётливо сформулировал принцип эквивалентности тепла и работы, а также приблизительно установил величину теплового эквивалента работы. Однако, записки Карно остались незамеченными и были опубликованы только через сорок лет после его смерти.

B период 1842—1850 гг. целый ряд исследователей почти одновременно устанавливает величину теплового эквивалента работы:

• Фон Майер, Юлиус Роберт в 1842 г. — по разности теплоёмкостей газов при постоянном давлении и постоянном объёме, на основе воззрений «о сохранении силы» (энергии);
• Джоуль в 1841—1843 гг. и Э. Ленц в 1844 — по тепловыделению в цепи электрического тока;
• Кольдинг и Джоуль в период 1843—1850 гг. — по тепловыделению при трении и т. п.

Установление принципа эквивалентности теплоты и работы было последним звеном на пути математического оформления первого начала термодинамики как общего закона сохранения энергии. Современная формулировка первого начала термодинамики для обратимых процессов и последующие построения принципиальных положений классической термодинамики, до второго начала термодинамики включительно, выполнены Рудольфом Клаузиусом (1850—1865) и Уильям Томсоном (лордом Кельвином (1851—1857). Усилиями этих учёных было произведено согласование выводов Карно, сделанных на базе теплородной теории, (теоремы Карно)с первым началом термодинамики. Кроме этого, P. Клаузиус получил новые результаты, составившие содержание второго начала термодинамики. Важнейшим моментом в построении первого начала, последовавшим вслед за открытием принципа эквивалентности, является введение понятия внутренней энергии тел (В. Томсон, 1851 г). Внутренняя энергия тел вначале рассматривалась как сумма внутреннего тепла и внутренней работы тела (Р.Клаузиус, «Механическая теория тепла», гл. I), однако, подобное определение в настоящее время не может быть принято, так как, очевидно, что ни тепло, ни работа в теле не содержатся. Тепло и работа, полученные телом извне, обращаются на повышение его внутренней энергии и, наоборот, за счет уменьшения внутренней энергии тела от него могут быть получены тепло и работа в рамках одной и той же суммы, но в различных соотношениях.

Основным содержанием термодинамики XIX века было исследование термодинамических циклов с точки зрения их коэффициента полезного действия и поиска путей его повышения, изучение свойств паров и газов, разработка термодинамических диаграмм для теплотехнических расчётов. В XX веке важной задачей стала разработка теории течения и истечения паров и газов в связи с той ролью, которую начали приобретать паровые и газовые турбины. Здесь выдающуюся роль сыграли труды Х. Лоренца и Л. Прандтля. Это направление развития науки представляло собой техническую термодинамику. Существенный вклад в развитие технической термодинамики внесли У. Ренкин, В. Джон, Р. Молье, и Л. Рамзин.

На грани XIX и XX веков началась ревизия построений классической термодинамики, которая относится главным образом к проблеме второго начала термодинамики Н. Н. Шиллер, 1900; К. Каратеодори, 1909; Т. Афанасьева-Эренфест, 1925; М. Планк). Она продолжилась в трудах К.Путилова, М. А. Леонтовича, А. А. Гухмана и Н. И. Белоконя. XX век характеризуется активным проникновением термодинамики в другие науки. Возникают новые направления в термодинамике, такие как физическая или общая термодинамика, химическая термодинамика, биологическая термодинамика (теория клетки), термодинамика электрических и магнитных процессов, релятивистская, квантовая, космическая термодинамики и т. д.

Параллельно классической (феноменологической) термодинамике развивалась статистическая физика|, которая сформировалась в конце XIX столетия на основании молекулярно-кинетической теории газов. Общим у этих двух наук является предмет изучения, но методы изучения совершенно различны. Если классическая термодинамика построена, в основном, на первом и втором, а также третьем началах термодинамики, то статистическая физика исходит из теорий строения вещества. «Законы классической или квантовой механики здесь распространяются на частицы, (атомы, молекулы), и путём статистических методов устанавливаются взаимосвязи между свойствами отдельных частиц и макрофизическими свойствами систем, состоящих из очень большого числа частиц»^[7].

Термодинамика использует понятия и обозначения, принятые в классической физике (механике), такие как масса, сила, объём, плотность, удельный объём и давление. Давление сплошных масс жидкостей, паров и газов, измеренное приборами барометрического типа называется [абсолютное давление|абсолютным давлением], а приборами манометрического типа ─ избыточным. В уравнения термодинамики входят только абсолютные давления. На практике для получения абсолютного давления к манометрическому давлению прибавляют барометрическое давление окружающей среды. Обычно для этой цели используют нормальное атмосферное давление. Понятия, заимствованные из физики, дополняются понятиями, свойственными термодинамике. К ним относятся: термодинамическая система, термодинамическое равновесие, термодинамические процессы, температура, теплота, термодинамическая работа, внутренняя энергия и т. д.

Термодинамическая система ─ исследуемый термодинамикой объект ─ представляет собой материальное содержимое выделенной области пространства (части Вселенной), отделённой реальной или условной оболочкой от внешней (окружающей) среды. В зависимости от возможности обмена веществом с внешней средой различают открытые и закрытые термодинамические системы. Системы, которые не могут обмениваться с внешней средой ни веществом, ни энергией, включающей излучение, называются изолированными. Термодинамическая система описывается рядом макроскопических переменных ─ физических величин (параметров), которые выражают свойства системы, например, объём, давление, температура, плотность, упругость, концентрация, поляризация, намагниченность и др. Для описания свойств системы используют макроскопические переменные ─ физические величины (параметры), которые называются функциями состояния. Функции состояния зависят только от состояния системы в данное время и не дают сведений о её предыстории, а, именно, каким образом система перешла в это состояние из предыдущего. Примерами функций состояния являются давление ${\displaystyle p}$, объём ${\displaystyle V}$, температура ${\displaystyle t}$, внутренняя энергия, ${\displaystyle U}$, энтальпия ${\displaystyle H}$, энтропия ${\displaystyle S}$, химический потенциал ${\displaystyle \mu }$ и др. Параметры состояния подразделяются на внутренние, описывающие свойства самой системы, и внешние, относящиеся к окружающей среде. Ряд параметров термодинамической системы можно непосредственно измерять. Параметры, измерение которых затруднительно или невозможно, получают путём вычислений. Примеры непосредственно измеряемых параметров: давление, ${\displaystyle p}$, объём ${\displaystyle V}$, температура ${\displaystyle t}$, количество молей вещества ${\displaystyle n}$, электрический потенциал ${\displaystyle \varpi }$ и т. п. Неизмеряемые (вычисляемые) термодинамические параметры ─ внутренняя энергия, ${\displaystyle U}$, энтальпия ${\displaystyle H}$, энтропия ${\displaystyle S}$, химический потенциал ${\displaystyle \mu }$ и др.

Термодинамическое равновесие есть такое (физическое, тепловое, химическое, фазовое) и тому подобное состояние термодинамической системы, при котором, в отсутствие внешнего воздействия, все её параметры сохраняют свои значения как угодно долго. Исходя из обобщённого человеческого опыта, изолированные системы обладают способностью переходить со временем в равновесное состояние. (В ряде источников это свойство возводится в ранг нулевого или общего начала термодинамики)^[8].

Равновесный процесс

Равновесным процессом называется непрерывная последовательность равновесных состояний, совершающихся в системе. Примером равновесного процесса может быть квазистатический (предельно замедленный процесс теплообмена между телами, находящимися в тепловом равновесии)

Обратимый процесс

Обратимым процессом называется процесс, который в условиях изолированной системы, то есть без внешнего воздействия, допускает возможность возврата этой системы из конечного состояния в начальное посредством какого-либо другого обратимого процесса. В обратимом процессе должны быть исключены необратимые процессы (трение, диффузия неравновесный теплообмен, и т. п.) ^[9].

Простая термодинамическая система, или простое тело, есть такая система, физическое состояние которой полностью определяется значениями двух независимых переменных ─ функций состояния простого тела, например, температура ${\displaystyle t}$ и удельный объём ${\displaystyle v}$, или давление ${\displaystyle p}$ и удельный объём ${\displaystyle v}$, или координаты термодинамической работы ${\displaystyle F_{i},X_{i}}$ и тому подобное.

Выражения зависимости трёх характеристик состояния простого тела ${\displaystyle (x,y,z)}$, которые допускают непосредственное измерение и являются попарно независимыми, называются уравнениями состояния этого тела: ${\displaystyle \varphi (x,y,z)=0}$.

Простыми телами называются изотропные тела, в частности: газы, пары, жидкости, плёнки и большинство твёрдых тел, находящихся в термодинамическом равновесии и не склонных к действию сил поверхностного натяжения, гравитационных и электромагнитных сил, а также химических превращений. Исследования простых тел в термодинамике представляют наибольший теоретический и практический интерес.

При построении термодинамики принимается, что все возможные энергетические взаимодействия между термодинамической системой и окружающей средой сводятся к передаче работы и теплоты.

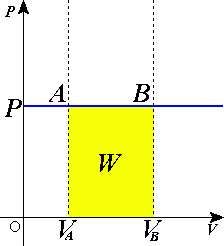
Первый способ передачи энергии, связанный с изменением внешних параметров системы, называется работой. Понятие механической работы термодинамика заимствует из физики (механики). В термодинамике вводится понятие обратимой или термодинамической работы. В случае простой термодинамической системы (простого тела) термодинамической работой называется работа сжатия тела в зависимости от абсолютного давления ${\displaystyle (p)}$ и изменения объёма ${\displaystyle (dV)}$:

${\displaystyle \delta A=pdV}$

или в интегральной форме:

${\displaystyle A_{1,2}=\int _{1}^{2}pdV=P_{m}(V2-V1)}$

Интегральное выражение величины термодинамической работы возможно только при наличии уравнения связи между давлением и объёмом.

Другой способ передачи энергии, без изменения внешних параметров, называется теплотой (теплом), а сам процесс передачи энергии — теплообменом. Теплообмен — это форма передачи энергии от одних тел к другим путём теплопроводности и излучения. Количество энергии, переданной системе с помощью работы, также носит название — работа ${\displaystyle (A)}$, а количество энергии, переданной посредством теплообмена, ─ количеством теплоты.^[10]

Исходное определение температуры: температура есть единственная функция состояния термодинамических систем (тел), определяющая направление самопроизвольного теплообмена между этими системами, то есть системы, находящиеся в тепловом равновесии, имеют одинаковую температуру в любой температурной шкале ${\displaystyle (T,t,\theta ).}$ Отсюда следует, что две системы, не соприкасающиеся между собой, но каждая из которых находится в тепловом равновесии с третьей системой (измерительный прибор), имеют одинаковую температуру. ^[11] Некоторые зарубежные источники называют это утверждение нулевым началом термодинамики.^[8][12] Температура в эмпирических шкалах измеряется различными приборами (термометрами), принцип действия которых основан на зависимости от температуры какого-либо свойства вещества: линейного расширения, давления, электрического сопротивления, термо-э.д.с., излучения и т. п..

С точки зрения молекулярно-кинетической теории температура определяется как физическая величина, пропорциональная средней кинетической энергии поступательного движения молекул идеального газа.

В температурных шкалах Фаренгейта и Цельсия в качестве реперных точек были выбраны температуры определённых процессов, например, температура замерзания и кипения воды при нормальных условиях (определённом значении давления). Потребность в более точных измерениях привела к усовершенствованию температурной шкалы. Существует самая низкая возможная температура, которую называют абсолютным нулём температуры. При температуре абсолютного нуля какое-либо тепловое движение в телах прекращается. Разработанная лордом Кельвином температурная шкала была выбрана таким образом, что температура тройной точки воды составляла 273,16 кельвина. При такой градации величина градуса Кельвина совпадает с величиной градуса Цельсия. Эта шкала температур получила название абсолютной. Абсолютная шкала температур используется в научных статьях, хотя в повседневной жизни шкала Цельсия удобней.

Внутренняя энергия системы есть полный запас энергии её внутреннего состояния, который определяется в зависимости от деформационных координат и температуры.

${\displaystyle u=u(x_{1},x_{2},...x_{n},t)}$

Полный запас энергии внутреннего состояния тел (системы) ${\displaystyle (u)}$ не может считаться известным ни на каком уровне развития естествознания. Однако, это обстоятельство не ограничивает уровня общности и точности математических выражений и расчётных соотношений термодинамики, поскольку в эти соотношения входят изменения внутренней энергии как функции состояния ${\displaystyle (du,\Delta u)}$. В связи с этим внутренняя энергия отсчитывается от принятого условного уровня, например, 0 °C и 760 мм рт. ст. ^[13]

Известно, что термодинамика — наука дедуктивная, черпающая главное своё содержание из двух исходных законов, которые носят название начал термодинамики. ^[14] Иными словами, под началами классической термодинамики подразумевают её основополагающие законы, однако, по вопросу, какие законы считать основополагающими, у учёных нет единого мнения. В целом можно насчитать от двух до пяти законов, претендующих на роль начал термодинамики. В англоязычной литературе наряду с традиционными первым и вторым началами некоторые авторы называют в качестве нулевого начала «общее» начало термодинамики — физический принцип, утверждающий, что вне зависимости от начального состояния изолированной системы, в конце концов, в ней установится термодинамическое равновесие, а также, что все части системы при достижении термодинамического равновесия будут иметь одинаковую температуру. Тем самым нулевое начало вводит также определение температуры. Р. Фаулер в 1931 г. сформулировал положение, согласно которому аксиома о существовании эмпирической температуры должна рассматриваться в качестве одного из начал термодинамики, за которым в монографии закрепилось не слишком удачное название «нулевое начало термодинамики». ^[8]. Некоторые авторы называют «общее начало» минус первым началом, а к нулевому началу относят закон транзитивности теплового равновесия, суть которого состоит в том, что, если имеются три равновесные термодинамические системы A, B и C, и, если системы A и B порознь находятся в равновесии с системой C, то системы A и B находятся в термодинамическом равновесии между собой. ^[15].

Первое начало термодинамики является математическим выражением закона сохранения энергии. Основным и неизменным подтверждением закона сохранения энергии служат результаты многовекового опыта познания природы. ^[16].

Второе начало термодинамики формулируется как объединённый принцип существования и возрастания некоторой функции состояния вещества — энтропии.

Под третьим началом термодинамики подразумевается теорема Нернста(1906 — 1911г), утверждающая недостижимость абсолютного нуля, которая формулируется также в другом виде: По мере приближения температуры к 0 K энтропия всякой равновесной системы при изотермических процессах перестаёт зависеть от каких-либо термодинамических параметров состояния и в пределе (T=0 K) принимает одну и ту же для всех систем универсальную постоянную величину, которую можно принять равной нулю. ^[17].

В отечественной литературе одни авторы к началам термодинамики относят первый и второй законы, а также теорему Нернста в качестве третьего начала термодинамики, другие — по традиции — началами термодинамики считают только её первый и второй законы. Вот, что пишет по этому поводу К. А. Путилов: «К этим двум началам … Нернст … присоединил третий закон, который, правда, не может претендовать на место третьего начала, но все же играет фундаментальную роль в термодинамике»^[18]. Отсюда следует, что к началам предъявляются очень высокие требования общности и научной ценности в плане построения термодинамики как науки. В этом смысле «общее» начало по существу выражает лишь принцип существования равновесной системы, а закон транзитивности теплового равновесия постулирует исходное понятие температуры в любой температурной шкале. В отличие от, так называемых, нулевого и минус первого начал, первое и второе начала являются источниками практически всех уравнений и неравенств термодинамики.

Особо следует остановиться на втором начале термодинамики. Если роль, которую играет в построении термодинамики первое начало, очевидна, то второе начало состоит из двух различных и неравноценных по своему содержанию и научной значимости частей.

Математические выражения принципа существования энтропии, совместно с первым началом, формулируются как равенства, и приводят к многочисленным точным дифференциальным соотношениям термодинамики, характеризующим свойства вещества. В отличие от них, выражения, вытекающие из принципа возрастания энтропии, всегда формулируются как неравенства и используются, главным образом, в исследованиях равновесия термодинамических систем и в определениях направления течения физических процессов, химических реакций и т. п. К тому же принцип возрастания энтропии является законом статистическим и справедливым лишь в мире положительных абсолютных температур, господствующих в наблюдаемой части Вселенной. Исходя из этого, представляется целесообразным сохранить статус «Начал» термодинамики за её первым и вторым законами, а также, за третьим законом, степень общности которого уступает первому и второму законам.

Исходным постулатом первого начала термодинамики является закон сохранения энергии:

Энергия изолированной системы сохраняет постоянную величину при всех изменениях, происходящих в этой системе, или, что то же, энергия не возникает из ничего и не может обратиться в ничто.

Важнейшим моментом в построении первого начала термодинамики является введение понятия внутренней энергии термодинамической системы (В. Томсон, 1851 г.). С точки зрения кинетической теории строения вещества внутренняя энергия термодинамической системы измеряется уровнем кинетической энергии и энергии взаимодействия материальных частиц этой системы, однако подобные воззрения недостаточны для объяснения всех известных явлений выделения энергии (химические, внутриатомные, внутриядерные процессы, электомагнитные, гравитационные и другие взаимодействия.) Вопрос об истинной природе внутренней энергии тел тесно связан с изучением строения материи, причём решение этой специальной задачи, базирующееся на представлениях о природе непосредственно ненаблюдаемых явлений, выходит за рамки возможностей лишь одного закона сохранения энергии. Поэтому в основу построений основных принципов термодинамики может быть положено лишь такое общее определение внутренней энергии тел, которое не ограничивает возможностей строгого построения термодинамики на базе постулатов общечеловеческого опыта.

Внутренней энергией термодинамической системы называется полный запас энергии её внутреннего состояния, определяемый в зависимости от деформационных координат и температуры:

$${\displaystyle u=u(x_{1},x_{2},...x_{n},t)}$$

Полный запас энергии внутреннего состояния тел ${\displaystyle (u)}$, вероятно, не может быть определён ни на каком уровне развития естествознания, но это обстоятельство не ограничивает уровня общности и точности математических выражений термодинамики, так как в эти соотношения входят лишь величины изменения внутренней энергии как функции состояния ${\displaystyle (du)}$, ${\displaystyle (\delta u)}$. В связи с этим внутренняя энергия отсчитывается от произвольно выбранного уровня (например, 0℃ и 760 мм рт. ст.).

При построении термодинамики принимается также, что все возможные энергетические взаимодействия между телами сводятся лишь к передаче тепла и работы. Соответственно формулируется исходное выражение первого начала термодинамики по внешнему балансу как математическое выражение закона сохранения энергии :

Изменение внутренней энергии тела или системы тел равно алгебраической сумме полученных (переданных) количеств тепла и работы или, что то же, тепло, полученное системой извне ${\displaystyle \delta Q^{*}}$ последовательно обращается на изменение внутренней энергии системы ${\displaystyle dU}$ и на выполнение (отдачу) внешней работы ${\displaystyle \delta A}$.

$${\displaystyle \delta Q^{*}=dU+\delta A^{*}}$$

В этой формулировке слово последовательно, добавленное Н. И. Белоконем, имеет следующий смысл. Если представить себе процесс, в котором внутренняя энергия остается неизменной ${\displaystyle (U=idem)}$, то вышеприведённое выражение первого начала (без слова последовательно) будет прочитано так: Тепло, полученное телом или системой, обращается на выполнение внешней работы. Такое утверждение верно лишь в том смысле слова, что численные величины тепла и работы равны. В действительности, положительная работа системы выполняется зa счёт изменения её деформационных координат (например, за счёт увеличения объёма), а подвод тепла лишь компенсирует происходящее при этом уменьшение внутренней энергии (уменьшение, эквивалентное выполненной внешней работе), так что в конечном итоге внутренняя энергия системы оказывается не изменившейся. Предупредительное указание (последовательно) предназначено для восстановления условной картины последовательного снижения и восстановления уровня внутpeнней энepгии при сопутствующем изменении потенциального состояния системы.

Знаки работы и тепла в уравнениях первого начала термодинамики:

${\displaystyle A>0}$ — выполнение рабочим телом положительной работы;

${\displaystyle Q>0}$ — сообщение тепла рабочему телу.

Классическая термодинамика, следуя Клаузиусу, вводит в уравнение первого начала выражение обратимой или термодинамической работы

Общий случай — $${\displaystyle \delta A_{i}=\sum F_{i}dx_{i}}$$

Простое тело — $${\displaystyle \delta A=PdV}$$

Выражения первого начала классической термодинамики действительны лишь для обратимых процессов. Это обстоятельство резко ограничивает возможности последующего развития принципов и практических приложений расчётных уравнений классической термодинамики. Поскольку все реальные процессы являются необратимыми, представляется целесообразным обобщить исходное уравнение первого начала термодинамики для обратимых и необратимых процессов. С этой целью Н. И. Белоконь, не снижая высокой степени общности исходных выражений первого начала, предложил для последующего развития основных принципов и расчётных уравнений термодинамики развернуть в них также выражения внешней работы. Для этого он ввёл понятие эффективной работы — ${\displaystyle \delta A^{*}}$, равной разности термодинамической работы ${\displaystyle \delta A_{i}=\sum F_{i}dx_{i}}$ и необратимых потерь ${\displaystyle \delta A^{**}}$

$${\displaystyle \delta A^{*}=\delta A-\delta A^{**}}$$

Потерянная в необратимых процессах работа ${\displaystyle \delta A^{**}}$ превращается в тепло внутреннего теплообмена тела ${\displaystyle \delta A^{**}}$; это тепло возвращается рассматриваемому телу или передается телам внешней системы, причём соответственно уменьшается итоговая величина подвода тепла извне:

$${\displaystyle \delta A^{**}=\delta Q^{**}}$$

Полное количество тепла, полученное телом ${\displaystyle \delta Q}$, характеризует термодинамический (приведённый), теплообмен тела и определяется как сумма двух величин — тепло, подведённое извне ${\displaystyle \delta Q^{*}}$, и тепло внутреннего теплообмена ${\displaystyle \delta Q^{**}}$:

$${\displaystyle \delta Q=\delta Q^{*}+\delta Q^{**}}$$^[19]

Исторически второе начало термодинамики возникло как рабочая гипотеза теплового двигателя, устанавливающая условия превращения теплоты в работу с целью достижения максимального эффекта такого превращения. Анализ второго закона термодинамики показывает, что малая величина этого эффекта — коэффициента полезного действия — является следствием не технического несовершенства тепловых двигателей, а особенностью теплоты, которая ставит определённые ограничения в отношении его величины. Под тепловым двигателем понимается термодинамическая система, с помощью которой можно осуществлять процесс превращения тепла в работу. Выбор принципа действия теплового двигателя основан на требовании непрерывности рабочего процесса и неограниченности его во времени. Это требование несовместимо с односторонне направленным изменением состоянием системы, при котором монотонно изменяются её параметры. Единственной, практически выполнимой, формой изменения системы, удовлетворяющей этому требованию, является периодически повторяющийся круговой процесс. Кроме тепловых двигателей, по круговым циклам работают холодильные машины и тепловые насосы. В русскоязычных источниках эти устройства объединяются одним понятием ─ тепловые машины.

Круговыми процессами, или циклами тепловых машин в термодинамике называются замкнутые процессы, характеризующиеся возвратом термодинамических систем ─ рабочих тел ─ в исходное состояние. ^[20]

Прямой цикл A используется в тепловом двигателе, схема которого представлена на рисунке 1. Тепло ${\displaystyle Q_{1}}$ подводится из источника высших температур ─ нагревателя ${\displaystyle t_{1}}$ и частично ${\displaystyle Q_{2}}$ отводится к источнику низших температур — холодильнику ${\displaystyle t_{2}}$. Работа, полученная в тепловом двигателе, согласно первому началу термодинамики, ${\displaystyle A}$ равна разности количеств подведённого и отведённого тепла:

$${\displaystyle A={Q_{1}}-{Q_{2}}}$$

Коэффициентом полезного действия (кпд) теплового двигателя называется отношение полученной работы ${\displaystyle A}$ к затраченному количеству тепла ${\displaystyle Q_{1}}$:

$${\displaystyle \eta ={\dfrac {A}{Q_{2}}}}$$

Обратный (холодильный) цикл B используется в холодильных машинах и тепловых насосах. В этом цикле происходит перенос тепла от источника низших температур ${\displaystyle Q_{2},t_{2}}$ к источнику высших температур ${\displaystyle t_{1},Q_{1}}$ (рис.1). Для осуществления этого процесса затрачивается внешняя работа, подводимая к холодильной машине.

Эффективность работы холодильной машины оценивается холодопроизводительностью— отношением перенесенного тепла ${\displaystyle Q_{2}}$ к затраченной работе ${\displaystyle A:}$

$${\displaystyle \epsilon _{x}={\dfrac {Q_{2}}{A}}={\dfrac {Q_{2}}{Q_{1}-Q_{2}}}}$$

Эффективность теплового насоса характеризуется коэффициентом преобразования (трансформации) или отопительным коэффициентом ${\displaystyle \epsilon _{o}}$, который определяется как отношение полученной нагреваемым телом теплоты ${\displaystyle Q_{1}}$ к затраченной для этого внешней работе ${\displaystyle A}$:

$${\displaystyle \epsilon _{o}={\dfrac {Q_{1}}{A}}}$$

Учитывая, что ${\displaystyle Q_{1}=Q_{2}+A}$, получим связь между отопительным и холодильным коэффициентами:

$${\displaystyle \epsilon _{o}=\epsilon _{x}+1}$$

Различают циклы работы реальных тепловых машин и теоретические циклы обратимых машин, в которых температуры внешних источников и рабочего тела совпадают, а внутренний теплообмен ${\displaystyle (\delta Q^{**}=0)}$ отсутствует. Диаграммы теоретических циклов обратимых тепловых машин (двигателей ─ рис. 1А и холодильных машин ─ рис. 1B) тождественны, но противоположно направлены. Обратимые процессы тепловых машин при бесконечно малых разностях температур внешних источников и рабочего тела можно представить как бесконечно замедленные квазистатические равновесные процессы.

В исследованиях теоретических циклов тепловых машин принимается в качестве рабочего тела идеальный газ, количество которого на всех стадиях цикла остаётся неизменным.

Цикл Карно (рис.2) в координатах P V ─ обратимый круговой процесс, осуществляемый между двумя внешними источниками тепла, имеющими разные температуры ─ нагревателем ─ ${\displaystyle T_{1}}$ и холодильником ─ ${\displaystyle T_{2}}$, характеризуется следующей последовательностью процессов: изотермическое расширение (1 ─ 2) при температуре ─ ${\displaystyle T_{1}}$, адиабатическое расширение (2 ─ 3), изотермическое сжатие (3 ─ 4) при температуре ${\displaystyle T_{2}}$ и, замыкающее цикл, адиабатическое сжатие (4 ─ 1).

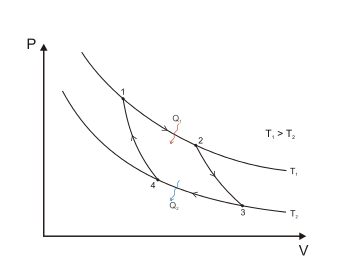
Теорема Карно утверждает, что КПД и холодопроизводительность термодинамического цикла Карно зависит от соотношения абсолютных температур рабочего тела в процессах сообщения и отъёма тепла, а, в случаях обратимого цикла, ─ от температур нагревателя и холодильника, и не зависит от вещества рабочего тела и конструкции тепловой машины. Коэффициент полезного действия термодинамического цикла Карно:

$${\displaystyle \eta =1-{\dfrac {Q_{2}}{Q_{1}}}=1-{\dfrac {T_{2}}{T_{1}}}={\dfrac {T_{1}-T_{2}}{T_{1}}}}$$

Холодопроизводительность термодинамического цикла Карно

$${\displaystyle \epsilon _{x}={\dfrac {Q_{2}}{A}}={\dfrac {T_{2}}{T_{1}-T_{2}}}}$$

Доказательство теоремы Карно (в рамках первого начала термодинамики) для частного случая, когда рабочим телом является идеальный газ, приведено в основной статье: Теорема Карно (термодинамика). В общем случае доказательство теоремы Карно возможно на основе использования принципа существования энтропии в рамках второго начала термодинамики.

Второе начало классической термодинамики традиционно формулируется как объединённый принцип существования и возрастания энтропии. (Здесь, и в дальнейшем, под термином энтропия подразумевается термодинамическая энтропия, (энтропия термодинамической системы). Энтропия является термодинамической функцией состояния, характеризующей состояние системы. Термин энтропия предложен Р. Клазиусом: еn — в, внутрь и trope или tropos — обращение, путь; в целом — обращение внутрь, мера обесценения энергии.

Принцип существования энтропии есть утверждение второго начала классической термодинамики о существовании некоторой функции состояния термодинамических систем — энтропии — ${\displaystyle S}$, дифференциал которой есть полный дифференциал ${\displaystyle dS}$, определяемый в обратимых процессах как величина отношения подведённого извне элементарного количества тепла ${\displaystyle \delta Q_{o}}$ к абсолютной температуре тела ${\displaystyle T}$:

$${\displaystyle dS_{o}={\frac {\delta Q_{o}}{T}}}$$

Математическое выражение принципа существования энтропии термодинамической системы эквивалентно описанию свойств этой системы, например, в построении принципа существования энтропии идеальных газов в рамках первого начала термодинамики, ^[21], однако, обоснование принципа существования энтропии для любых термодинамических систем возможно только в рамках второго начала термодинамики.

Принцип возрастания энтропии есть утверждение второго начала классической термодинамики о неизменном возрастании энтропии изолированных систем во всех реальных (необратимых) процессах изменения состояния этих систем. (В обратимых процессах изменения состояния изолированных систем их энтропия не изменяется).

$${\displaystyle dS\geq 0}$$

Энтропия является термодинамической функцией состояния, которая зависит от нескольких независимых параметров, однозначно определящих состояние термодинамической системы, но не зависит от того, каким путём было достигнуто это состояние. Физический смысл энтропии достаточно сложен и не поддаётся непосредственному восприятию. Он напрямую не вытекает из её математического выражения, а величина энтропии не может быть непосредственно измерена прибором. Физический смысл энтропии может быть выяснен при рассмотрении различных необратимых физических, химических, ядерных, биологических и других процессов, например: трение, электронагрев, неравновесный теплообмен, диффузия диссипация (рассеяние) энергии. В общем случае можно говорить, что энтропия это мера необратимости реального термодинамического процесса, мера обесценения энергии с точки зрения возможности получения работы.

Как уже отмечалось, уровень общности принципов существования и возрастания энтропии различен. На принципе существования энтропии основана система равенств термодинамики — её важнейшие дифференциальные соотношения, которые широко используются при изучении термодинамических процессов и физических свойств веществ. Научную ценность принципа существования энтропии трудно переоценить.

Принцип возрастания энтропии изолированных систем статистический. Он характеризует наиболее вероятное направление изменения изолированных термодинамических систем, течения физических процессов и химических реакций. На этом принципе основана система неравенств термодинамики.

Учение об идеальных газах восходит к открытым в результате не вполне точных экспериментальных исследований в XVII—XIX веках газовых законов: Бойля — Мариотта, Гей-Люссака и Шарля, а также сформулированному Клапейроном объединённому уравнению газового состояния. В те времена считалось, что газы, в отличие от паров, несжижаемы и сохраняют своё газообразное состояние в любом температурном диапазоне. Развитие криогенной техники опровергло эти представления. Выяснилось, что все без исключения реальные газы представляют собой агрегатное состояние соответствующих веществ и, по сути, являются перегретыми парами, достаточно удалёнными от точки кипения и критической точки, а точным уравнением состояния газа может быть уравнение состояния простого тела. Однако, газовые законы сохранились в термодинамике и в её технических приложениях как законы идеальных газов — предельных (практически недостижимых) состояний реальных газов. ^[22] Под идеальными газами в классической термодинамике подразумеваются гипотетические (реально не существующие) газы, строго подчиняющиеся уравнению Клапейрона. (В отечественной литературе его называют также уравнением Клапейрона — Менделеева). Уравнение Клапейрона также было теоретически выведено при некоторых допущениях на основе молекулярно — кинетической теории газов (Августом Крёнигом в 1856 г.^[23] и Рудольфом Клаузиусом в 1857 г.) Существует заблуждение, связанное с изучением термодинамики в курсах общей физики и в средней школе, где нередко не разделяют классический подход к изучению термодинамики и молекулярно-кинетическую теорию. При этом создаётся ложное впечатление, будто законы идеальных газов являются законами термодинамики. На самом деле, законами классической термодинамики являются её «Начала». Идеальный газ, является одним из объектов, который исследуется термодинамикой. Что касается реальных газов, то их состояние приблизительно описывается различными теоретическими и эмпирическими уравнениями, например, уравнением Ван-дер-Ваальса. Точным уравнением состояния реального газа может быть уравнение состояния простого тела.

Закон Бойля ─ Мариотта.

Роберт Бойль в 1662 г. сформулировал результаты своих экспериментов по сжиманию воздуха при постоянной температуре следующим образом:

Давления и объёмы находятся в обратном отношении:

$${\displaystyle {\frac {p_{1}}{p_{2}}}={\frac {V_{2}}{V_{1}}}.}$$

или

$${\displaystyle p_{1}V_{1}=p_{2}V_{2}}$$,

где ${\displaystyle V_{1},p_{1},}$ — начальные величины объёма и давления газа; ${\displaystyle V_{2},p_{1}}$ — их конечные величины.

Независимо от Бойля к такому соотношению пришёл Эдм Мариотт в 1676 г.

Как закон физического состояния идеальных газов закон Бойля — Мариотта формулируется следующим образом:

Произведение абсолютного давления данной массы идеального газа при постоянной температуре сохраняет постоянную величину, или что то же, произведение абсолютного давления на объём данной массы идеального газа зависит только от температуры газа и от его химической природы.

$${\displaystyle pV=C}$$,

где ${\displaystyle C}$ — постоянная, в данных условиях, величина;

или

${\displaystyle pV=f(t)}$.^[24]

Закон Гей-Люссака:

Объём данной массы идеального газа при постоянном давлении изменяется линейно с изменением температуры.

$${\displaystyle V=V_{0}(1+\alpha _{0}t)}$$, ^[25].

где: ${\displaystyle V}$ ─ объём массы газа ${\displaystyle m}$ при температуре ${\displaystyle t}$°C и постоянном давлении ${\displaystyle p}$ ;

${\displaystyle V_{0}}$ ─ объём той же массы газа при температуре ${\displaystyle 0}$°C и при том же давлении;

${\displaystyle t}$─ температура в градусах Цельсия.

${\displaystyle \alpha _{0}}$─ температурный коэффициент объёмного расширения идеальных газов, одинаковый для всех идеальных газов при любых давлениях.

${\displaystyle \alpha _{0}={\frac {1}{273,15}}{K^{-1}}}$.

Абсолютная температура ${\displaystyle T}$:

${\displaystyle T=t+{\frac {1}{\alpha _{0}}}}$

С учётом этого, выражение ${\displaystyle (1+\alpha _{0}t)}$ может быть преобразовано:

$${\displaystyle (1+\alpha _{0}t)=1+{\frac {t}{273,15}}={\frac {273,15+t}{273,15}}={\frac {T}{273,15}}}$$

откуда:

${\displaystyle V=V_{0}{\frac {T}{273,15}}}$

Обозначив ${\displaystyle T_{0}=273,15K=0^{0}C}$, получим другое выражение закона Гей-Люссака:

$${\displaystyle {\frac {V}{V_{0}}}={\frac {T}{T_{0}}}}$$.

При неизменной массе газа и постоянном давлении объём газа прямо пропорционален абсолютной температуре.

Закон Шарля.

Давление ${\displaystyle p}$ данной массы газа при постоянном объёме пропорционально абсолютной температуре.

$${\displaystyle {\frac {p}{T}}=const}$$ при ${\displaystyle V=const}$.

Объединённое уравнение состояния идеального газа (уравнение Клапейрона):

Допустим, что в начальном состоянии некоторая масса газа ${\displaystyle m}$ имеет давление ${\displaystyle p_{1}}$, объём ${\displaystyle V_{1}}$: и температуру ${\displaystyle T_{1}}$. Оставив давление постоянным, нагреем газ до температуры ${\displaystyle T_{2}}$. Его объём увеличится и станет ${\displaystyle V'}$ (промежуточное состояние). Переход газа из начального состояния в промежуточное произошёл по закону Гей-Люссака:

$${\displaystyle {\frac {V_{1}}{V'}}={\frac {T_{1}}{T_{2}}}}$$.

Оставив температуру газа без изменения, уменьшим его объём до ${\displaystyle V_{2}}$, при котором давление стало ${\displaystyle p_{2}}$ (конечное состояние). Переход газа из промежуточного состояния в конечное произошёл по закону Бойля-Мариотта:

${\displaystyle p_{1}V'=p_{2}V_{2}}$,

Выразив значения ${\displaystyle V'}$ из первого и второго равенств:

${\displaystyle V'={\frac {V_{1}T_{2}}{T_{1}}}}$

${\displaystyle V'={\frac {p_{2}V_{2}}{p_{1}}}}$

и приравняв их:

${\displaystyle {\frac {V_{1}T_{2}}{T_{1}}}={\frac {p_{2}V_{2}}{p_{1}}}}$

Получим (при ${\displaystyle m=const}$)

$${\displaystyle {\frac {p_{1}V_{1}}{T_{1}}}={\frac {p_{2}V_{2}}{T_{2}}}={\frac {pV}{T}}=const}$$

Это уравнение, связывающая объём, давление, температуру и массу газа, представляет собой объединённый закон Бойля ─ Мариотта и Гей-Люссака или уравнение Клапейрона.

Перепишем уравнение Клапейрона для одного киломоля газа при нормальных условиях. В этом случае величины ${\displaystyle p}$, ${\displaystyle V}$, ${\displaystyle T}$ будут постоянными: ${\displaystyle p=101325}$ Па (760 мм рт. ст). ${\displaystyle T=273,15K}$ , объём 1 киломоля газа ${\displaystyle V_{0}=22,414M^{3}}$. При таком условии отношение ${\displaystyle {\frac {pV_{0}}{T}}}$ будет всегда равно одной и той же величине:

$${\displaystyle h{\frac {pV_{0}}{T}}=R}$$

или

$${\displaystyle pV_{0}=RT}$$,

где ${\displaystyle R}$ ─ характеристическая постоянная идеального газа, равная работе одного киломоля газа в изобарическом процессе при нагревании его на один градус.

${\displaystyle R={\frac {pV_{0}}{T}}=8314}$дж/кмоль·К

Для ${\displaystyle n}$ киломолей уравнение примет вид: $${\displaystyle pV=nRT}$$,

где ${\displaystyle V=nV_{0}}$

Учитывая, что

${\displaystyle n={\frac {m}{\mu }}}$,

где ${\displaystyle \mu }$ молекулярная масса газа,

получим:

$${\displaystyle pV={\frac {m}{\mu }}RT}$$,

Уравнение состояния идеальных газов в таком виде было выражено Д. И. Менделеевым и называется ─ уравнение Клапейрона ─ Менделеева.

Уравнение состояния идеальных газов Клапейрона может быть получено при некоторых допущениях на основе молекулярно — кинетической теории газов. Основной предпосылкой для такого вывода: идеальные газы представляют собой систему материальных точек не испытывающих воздействия сил взаимного притяжения, отталкивания и т. п. А газовые законы Бойля ─ Мариотта, Гей-Люссака и Шарля могут быть теоретически выведены из уравнения Клапейрона.

Термодинамическая сущность теплофикации состоит в комбинированной выработке электроэнергии и энергии для тепловых потребителей без потерь с циркуляционной водой^[26].

Теплоснабжение крупных тепловых потребителей часто осуществляют при отпуске пара из котлов. Сухой насыщенный пар из парового котла поступает к потребителю, конденсируется, и конденсат насосом снова подаётся в котел. Количество энергии, отдаваемой потребителю, в этой схеме теоретически равно количеству энергии, израсходованной в котле в котле на получение пара, поэтому без учета потерь коэффициент полезного использования энергии равняется 1.

Как правило, тепловым потребителям требуется энергия низкого температурного потенциала. Это привело к идее создания теплоэлектроцентралей (ТЭЦ), вырабатывающих электроэнергию и удовлетворяющих тепловых потребителей. На ТЭЦ устанавливают энергетические парогенераторы высокого давления с перегревом пара. Из парогенератора пар поступает в турбину, где адиабатно расширяется. Из турбины пар направляется к тепловому потребителю, где конденсируется, отдавая энергию. Получающийся конденсат насосом возвращается в парогенератор.

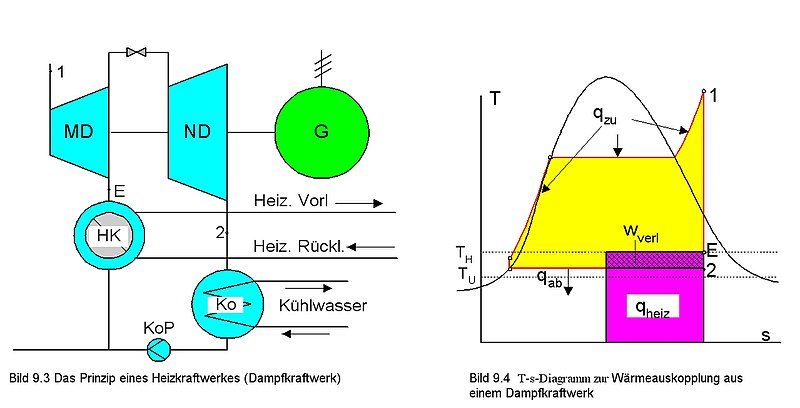
На T, s-диаграмме изображён теоретический цикл ТЭЦ с противодавленческой турбиной. Конечное давление в турбине определяется требованиями удовлетворения тепловых потребителей энергией нужного температурного потенциала. Это давление значительно выше давления в конденсаторе конденсационной турбины (поэтому такая турбина и называется противодавленческой), поэтому при одинаковых начальных параметрах пара термический КПД цикла ТЭЦ существенно снижается по сравнению с конденсационной электростанцией (КЭС). Однако при этом нет теплового отброса^[27], так что полный коэффициент использования энергии теоретически равен 1 и не зависит от внутренних потерь в турбине.

Газотурбинная установка (ГТУ) конструктивно объединяет газовую турбину и электрический генератор. Воздух из компрессора (1) и топливо (газовое иди жидкое) подают в камеру сгорания (2), откуда поток раскаленных газов (рабочее тело) направляют на рабочее колесо турбины (3), приводящей в действие компрессор и электрогенератор (4). Процесс горения топлива рассматривают как процесс подвода энергии к рабочему телу. В теории термодинамических циклов газотурбинные установки классифицируют по характеру подвода энергии к рабочему телу: со сгоранием топлива при постоянном давлении и со сгоранием при постоянном объёме^[28].

Простая ГТУ с подводом теплоты при постоянном давлении работает по циклу Брайтона: атмосферный воздух адиабатно сжимают в компрессоре; в камере сгорания происходит изобарный нагрев рабочего тела; в газовой турбине рабочее тело адиабатно расширяется; отработанные газы изобарно отводятся в атмосферу. Хотя схема простой ГТУ является разомкнутой, но идеальный цикл этой установки на термодинамических диаграммах (p, V-диаграмме Эндрюса, T, s-диаграмме) изображают как замкнутый и состоящий из двух изобар и двух адиабат, то есть массу рабочего тела считают неизменной. При этом горение рассматривают как изобарный подвод энергии к рабочему телу извне через стенки корпуса установки, а выброс отработанных газов в атмосферу полагают условно замыкающим цикл изобарным отводом энергии от рабочего тела к холодному тепловому резервуару. Рабочее тело представляет собой воздух (изменением его состава при горении пренебрегают), рассматриваемый как идеальный газ^[29][30][31].

Особенностью реактивных двигателей является непрерывность всех процессов, осуществляемых в отдельных их элементах. Воздушно-реактивный двигатель (ВРД) в качестве рабочего тела использует смесь забираемого из атмосферы воздуха и продуктов окисления топлива кислородом, содержащимся в воздухе. За счёт реакции окисления рабочее тело нагревается и, расширяясь, истекает из двигателя с большой скоростью, создавая реактивную тягу^[32].

В прямоточном ВРД (ПВРД) сжатие воздуха, поступающего из атмосферы в камеру сгорания, обусловлено скоростным напором воздушного потока. Цикл ПВРД (Цикл Брайтона) состоит из адиабаты сжатия воздуха в диффузоре, изобары процесса сгорания, адиабаты расширения в сопле и замыкающей цикл изобары охлаждения продуктов сгорания при атмосферном давлении. С точки зрения термодинамики цикл ПВРД аналогичен циклу газотурбинной установки со сгоранием при постоянном давлении^[33].

В турбокомпрессорном (турбореактивном) воздушно-реактивном двигателе (ТРД) сжатие воздуха осуществляется как в результате скоростного напора, так и при помощи осевого компрессора, приводимого в движение газовой турбиной, с которой он имеет общий вал. Теоретический цикл ТРД аналогичен циклу прямоточного ПВРД и состоит из тех же процессов, с тем лишь различием, что в ТРД компрессор обеспечивает дополнительное сжатие воздуха^[34].

Пульсирующий прямоточный воздушно-реактивный двигатель (ПуВРД) снабжён специальным устройством клапанного типа, в результате чего камера сгорания может быть изолирована от диффузора и сопла, так что процесс сгорания осуществляется при постоянном объёме. Для этого двигателя характерна периодичность действия, чем и объясняется его название. Цикл ПуВРД (Цикл Хамфри) состоит из адиабаты сжатия воздуха в диффузоре, изохоры процесса сгорания, адиабаты расширения в сопле и замыкающей цикл изобары охлаждения продуктов сгорания при атмосферном давлении. Цикл ПуВРД аналогичен циклу газотурбинной установки со сгоранием при постоянном объёме^[35].

Бесклапанные ПуВРД работают по циклу Ленуара.

ПуВРД вследствие значительно большего давления в конце процесса сгорания топлива имеет больший термический КПД по сравнению с ПВРД, но не получил широкого распространения из-за конструкционной сложности^[36].

Двигатель внутреннего сгорания (ДВС) представляет собой тепловую машину, в которой подвод энергии к рабочему телу осуществляется за счет сжигания топлива внутри самого двигателя. Рабочим телом в таких двигателях является на первом этапе воздух или смесь воздуха с легковоспламеняющимся топливом, а на втором этапе — продукты сгорания этого жидкого или газообразного топлива. Давления рабочего тела не слишком высоки и температуры его намного превышают критические, что позволяет с хорошим приближением рассматривать рабочее тело как идеальный газ; это существенно упрощает термодинамический анализ цикла^[37].

В технической термодинамике реальные процессы в ДВС отождествляют с термодинамическими циклами, лежащими в их основе. Реальные циклы двигателей внутреннего сгорания являются разомкнутыми, ибо в них рабочее тело поступает извне и по окончании цикла выбрасывается в атмосферу, а в каждом реальном цикле участвует новая порция рабочего тела. Поскольку в горючей смеси, подаваемой в цилиндр двигателя (воздух + топливо), количество топлива относительно невелико по сравнению с количеством воздуха, для удобства анализа обычно принимают, что цикл двигателя внутреннего сгорания является замкнутым, рабочим телом цикла является воздух, количество которого в двигателе остается неизменным. Процессы горения топлива рассматривают как процессы подвода энергии к рабочему телу от внешнего горячего источника через стенку цилиндра^[38].

Циклы поршневых двигателей внутреннего сгорания, имеющих различные принципы работы, различают по характеру подвода энергии к рабочему телу^[38]:

• изохорные циклы с подводом энергии при постоянном объёме, например, цикл Отто;
• изобарные циклы с подводом энергии при постоянном давлении, например, цикл Дизеля;
• смешанные циклы с подводом энергии вначале при постоянном объёме, а затем при постоянном давлении, например, цикл Тринклера.

Термодинамический анализ идеализированных циклов ДВС не учитывает, что в реальных циклах рабочее тело (в первых двух тактах — это воздух в цикле Дизеля и в цикле со смешанным сгоранием или горючая смесь в цикле Отто, в последующих тактах — это воздух и продукты сгорания) по своим свойствам отличается от идеального газа с постоянной теплоемкостью; вследствие неизбежного трения процессы адиабатного сжатия и расширения происходят не по изоэнтропе, а с ростом энтропии; принудительное охлаждение стенок цилиндра ещё больше увеличивает отклонение этих процессов от изоэнтропных; сгорание происходит за малые, но всё же конечные промежутки времени, в течение которых поршень успевает несколько переместиться, так что условие изохорности процесса сгорания выполняется не совсем строго; имеют место механические потери в механизме и т. д. В силу перечисленных причин фактические КПД тепловых машин существенно меньше КПД соответствующих идеализированных циклов^[39].

Магнитогидродинамический генератор (МГД-генератор), использующий ионизированный газ в качестве рабочего тела и работающий по открытому циклу, кроме первичного разомкнутого контура имеет вторичный замкнутый паросиловой контур, в котором энергия продуктов сгорания после канала МГД-генератора используется для выработки электроэнергии генератором, приводимым в действие паровой турбиной.

Тепловой цикл первичного контура состоит из следующих процессов^[40]: 1) адиабатного сжатия воздуха в компрессоре; 2) изобарного подвода теплоты в воздухоперегревателе; 3) изобарного подвода теплоты в камере сгорания; 4) адиабатного расширения в канале МГД-генератора; 5) изобарного отвода теплоты в воздухоподогревателе; 6) изобарного отвода теплоты в парогенераторе; 7) изобарного отвода теплоты в окружающую среду (с продуктами сгорания, выбрасываемыми в атмосферу). Цикл вторичного паросилового контура особенностей не имеет, а высокая температура продуктов сгорания топлива позволяют пароводяному циклу иметь параметры, соответствующие стандартным характеристикам крупных паротурбинных установок^[41].

Термоэлектрический генератор основан на использовании эффекта Зеебека — возникновения ЭДС в замкнутой электрической цепи, состоящей из последовательно соединённых разнородных проводников, контакты между которыми имеют различные температуры.

Электрохимический генератор (топливный элемент) основан на прямом электрохимическом преобразовании энергии подаваемых извне топлива и окислителя в электричество, поэтому его описывают теми же термодинамическими соотношениями, что и гальванический элемент. Величина КПД электрохимических генераторов достигает 70 %, однако их широкое распространение сдерживается высокой стоимостью^[41].

К комбинированным циклам относят^[42]:

• бинарные ртутно-водяные циклы;
• парогазовые циклы;
• парогазовые циклы с регенерацией;
• парогазовые циклы с МГД-генераторами.

Особенности получения теплоты от реактора, а также особенность экономики АЭС, где, в отличие от обычных электростанций, затраты на топливо составляют лишь малую часть себестоимости вырабатываемой электроэнергии, приводят к тому, что чаще всего верхняя граница температурного интервала, в котором осуществляется цикл, намного ниже, чем для циклов обычных электростанций. В этих условиях становится целесообразным использование цикла с влажным водяным паром^[43].

В зависимости от типа реактора, используемого теплоносителя и других факторов тепловая схема атомной электростанции (АЭС) может быть одно-, двух- и трёхконтурной. Одноконтурные и двухконтурные схемы применяют на АЭС с реакторами на тепловых нейтронах, трёхконтурные — на АЭС с реакторами на быстрых нейтронах^[44].

В одноконтурной схеме вода и её пар одновременно являются теплоносителями и замедлителями в реакторах и рабочим телом в паротурбинной установке. Вода, контактируя с тепловыделяющими элементами с высокой радиоактивностью, сама становится радиоактивной. Образующийся в активной зоне реактора пар направляется в турбину, где совершает работу. Турбина является приводом электрогенератора, вырабатывающего электрическую энергию. Отработанный пар поступает в конденсатор, а конденсат питательным насосом снова подается в реактор. Достоинства одноконтурной схемы состоят в её простоте и тепловой экономичности, недостатком является то, что в этой схеме всё оборудование работает в радиационно-активных условиях^[45].

В двухконтурной схеме АЭС теплоноситель и рабочее тело движутся по разным контурам, общим элементом которых является парогенератор (теплообменник). В качестве теплоносители, отводящего теплоту, выделяемую в реакторе, могут использоваться вода, жидкие металлы (натрий), органические соединения и газы (гелий). Всё оборудование первого контура радиоактивно, поэтому оно отделено от остальной части электростанции специальной биологической защитой; циркулирующее во втором контуре рабочее тело практически не радиоактивно^[46].

Для реакторов на быстрых нейтронах, имеющих высокую концентрацию делящихся материалов в активной зоне, а, следовательно, и большую удельную тепловую мощность, очень важны как эффективность передачи теплоты в активной зоне реактора, так и соблюдение требований безопасности. Поэтому в АЭС на быстрых нейтронах применяют трёхконтурную тепловую схему, в которой циркулирующий в первом контуре жидкий натрий отдаёт теплоту нерадиоактивному теплоносителю, тоже натрию, и возвращается в реактор. Нагретый в промежуточном теплообменнике теплоноситель второго контура поступает в парогенератор, где отдает теплоту рабочему телу третьего контура — воде, которая превращается в пар. Натрий насосом возвращается в промежуточный теплообменник, а водяной пар направляют в паровую турбину, являющуюся приводом электрогенератора. Пар из турбины направляют в конденсатор, а конденсат насосом возвращают в парогенератор^[47].

Дополнительный тепловой контур повышает надежность и безопасность АЭС, однако приводит к значительному увеличению капитальных вложений.

Холодильные установки применяют для понижения температуры тел ниже температуры окружающей среды и поддержания этой низкой температуры. Процесс охлаждения тел с температурой окружающей среды и ниже основан на отборе рабочим телом — холодильным агентом — энергии от холодного тела и её передаче более нагретому телу (окружающей среде). Согласно второму закону термодинамики это возможно, если процесс охлаждения протекает одновременно с компенсирующим его процессом совершения работы или процессом перехода энергии от более нагретого тела к менее нагретому^[48].

Тепловой насос — это «холодильная машина наоборот», агрегат, работающий по тому же принципу, что и холодильная машина, но используемый не для целей охлаждения, а для целей отопления, то есть повышения температуры тел выше температуры окружающей среды и поддержания этой более высокой температуры^[49].

В холодильных установках и тепловых насосах энергия отбирается от низкотемпературного источника за счёт совершения работы в обратном цикле. Самым термодинамически совершенным является обратный цикл Карно^[48]. Термодинамической характеристикой эффективности обратного цикла в холодильной машине служит холодильный коэффициент^[50][51], а в тепловом насосе — коэффициент трансформации энергии (он же коэффициент преобразования теплового насоса^[52], он же коэффициент преобразования теплоты^[53], он же отопительный коэффициент^[54][53], он же коэффициент теплоиспользования^[55]).

В термоэлектрических холодильных установках, использующих эффект Пельтье, и в установках, основанных на термомагнитном эффекте Эттингсгаузена, холодильный агент не используется^[56].

• Неравновесная термодинамика
• Термодинамика
• Химическая термодинамика

• МГД-генераторы  (неопр.).