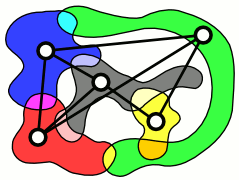
Трапецеидальный граф
В теории графов трапецеидальными графами называются графы пересечений трапеций, все параллельные стороны которых лежат на двух прямых. Этот класс графов содержится в классе графов косравнимости и содержат интервальные графы и графы перестановки в качестве подклассов. Граф является трапецеидальным в том и только в том случае, когда существует набор трапеций, соответствующих вершинам графа, и две вершины графа соединены ребром в том и только в том случае, когда соответствующие вершинам трапеции пересекаются. Трапецеидальные графы были введены в рассмотрение в 1988 году Даганом (Ido Dagan), Колумбиком (Martin Charles Golumbic) и Пинтером (Ron Pinter). Для этих графов существуют алгоритмы со временем работы для раскраски графа, для поиска взвешенных независимых множеств, кликовых покрытий и максимальных взвешенных клик.
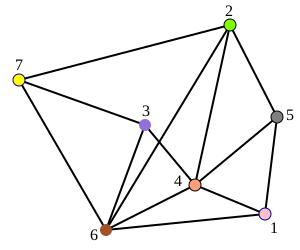
Определение и характеристики
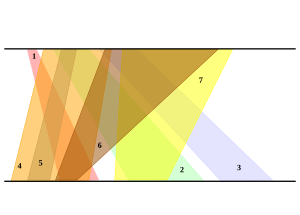
Пусть заданы две параллельные прямые. На этих прямых задаются трапеции, у которых две вершины лежат на одной прямой, а две другие – на другой прямой. Граф является трапецеидальным в том и только в том случае, когда существует набор трапеций, соответствующих вершинам графа, и две вершины графа соединены ребром в том и только в том случае, когда соответствующие вершинам трапеции пересекаются. Размерностью частично упорядоченного множества называется наименьшее число d полных порядков , таких, что . Граф несовместимости частично упорядоченного множества — это неориентированный граф , в котором вершина x смежна вершине y в G в том и только в том случае, когда x и y несравнимы в P. Неориентированный граф является трапецеидальным графом в том и только в том случае, когда он является графом несравнимости частично упорядоченного множества с размерностью не более 2.[1]
Приложения
Задачи поиска максимальных клик и раскраски трапецеидальных графов связаны с задачей прокладки проводящих каналов при проектировании интегральных схем. Если заданы некоторые помеченные точки на верхней и нижней сторонах платы, точки с одинаковыми пометками будут соединены в общую сеть. Эта сеть может быть представлена трапецией, которая содержит крайние (левые и правые) точки с одной и той же пометкой. Сети можно проложить без пересечения в том и только в том случае, если трапеции не пересекаются. Таким образом, число необходимых слоёв, нужных для прокладки проводников без пересечений, равно хроматическому числу графа.
Эквивалентные представления
Представление трапециями
Трапеции можно использовать для представления графа, исходя из определения.
Представление прямоугольниками
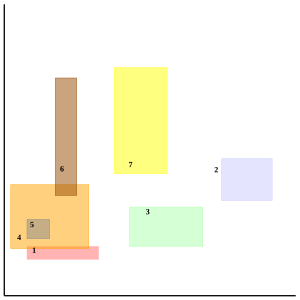
Представление доминирующими прямоугольниками отображает точки одной прямой как точки на оси x, а точки другой прямой — как точки на оси y евклидовой плоскости. Тогда любая трапеция соответствует прямоугольнику на плоскости. Говорят, что в RK, x доминируется y, что записывается как x < y, если xi меньше yi для i = 1, …, k. Мы говорим, что прямоугольник b доминирует над b’, если нижний угол b доминирует над верхним углом b’. Мы говорим, что два прямоугольника сравнимы, если один доминирует над другим. Таким образом, две трапеции не пересекаются в точности тогда, когда соответствующие им прямоугольники сравнимы. Представление прямоугольниками полезно, поскольку отношение доминирования позволяет применять алгоритм развёртки[англ.].[2] Представление графа с рисунка 1 в виде прямоугольников приведено на рисунке 3.
Битолерантные графы
Битолерантные графы — это графы несравнимости битолерантного порядка. Порядок называется битолерантным в том и только в том случае, когда существуют интервалы Ix и вещественные числа t1(x) и tr(x), присвоенные каждой точке x таким образом, что x < y в тои и только в том случае, когда перекрытие Ix и Iy меньше, чем tr(x), и t1(y) и середина Ix меньше, чем середина Iy.[3] В 1993 Лэнгли (Langley) показал, что ограниченные битолерантные графы эквивалентны классу трапецеидальных графов.[4]
Связь с другими семействами графов
Класс трапецеидальных графов содержит интервальные графы и графы перестановок и эквивалентен графам несравнимости частично упорядоченных множеств, имеющих размерность порядка не больше двух. Графы перестановок можно рассматривать как частный случай трапецеидальных графов, если трапеции свести к линиям (то есть к трапециям, у которых длины параллельных сторон нулевые).
Как и все графы несравнимости, трапецеидальные графы являются совершенными.
Круговые трапецеидальные графы

Круговые трапецеидальные графы — это класс графов, предложенный Фелснером (Felsner) и др. в 1993. Эти графы являются суперклассом трапецеидальных графов и содержат циркулянтные графы и графы дуг окружности. Круговая трапеция — это область круга между двумя непересекающимися хордами, а круговой трапецеидальный граф — это граф пересечений семейства круговых трапеций. Круговое представление графа представлено на рисунке 4. Существует алгоритм со временем работы для решения задачи поиска независимого множества максимального веса и алгоритм со временем работы для задачи поиска максимальной по весу клики.
k-трапецеидальные графы
k- трапецеидальные графы — это обобщение трапецеидальных графов на большие размерности пространства. Они были предложены Фелснером и основываются на определении доминантных многомерных прямоугольников. В этих графах вершина x соответствует вектору . Используя (k − 1)-мерные сортировочные деревья для хранения и выборки координат, алгоритмы Фелснера решают задачи нахождения хроматического числа, максимальной клики и максимального независимого множества за время .
Алгоритмы
Алгоритмы для трапецеидальных графов следует сравнивать с алгоритмами более общих графов косравнимости. Для этого, более широкого класса графов, задачи поиска максимального независимого множества и минимального кликового покрытия можно решить за время .[5] Даган (Dagan) и др. сначала предложили алгоритм раскраски трапецеидальных графов за время , где n — это число вершин, а k —хроматическое число графа. Позднее, используя представление трапецеидальных графов прямоугольниками, Фелснер опубликовал алгоритмы поиска хроматического числа, взвешенного независимого множества, кликового покрытия и максимальной взвешенной клики за время . Все эти алгоритмы требуют память размером . Эти алгоритмы основываются на доминировании в представлении прямоугольниками, что позволяет применить алгоритмы развёртки. Предложенные Фелснером алгоритмы используют сбалансированные деревья, позволяющие выполнять операции вставки, удаления и запроса за время , что и даёт результирующее время .
Распознавание
Для определения, является ли граф трапецеидальным, ищется транзитивная ориентация на дополнении графа . Поскольку трапецеидальные графы являются подмножеством косравнимых графов, если является трапецеидальным, его дополнение должно быть графом сравнимости. Если транзитивная ориентация на дополнении не существует, граф не является трапецеидальным. Если же будет найдена, проверяется, будет ли порядок, задаваемый трапецеидальным порядком. Самый быстрый алгоритм распознавания трапецеидального порядка был предложен Макконнеллом (McConnell) и Спинрадом (Spinrad) в 1994 со временем работы . Процесс сводит вопрос о размерности частичного порядка (не превышает ли он 2) к задаче покрытия соответствующего двудольного графа цепями (графами без порождённых 2K2 подграфов).[6] Как показали Мертциос (Mertzios) и Корнейл (Corneil), если использовать разделение вершин, задачу распознавания трапецеидальных графов можно решить за время , где обозначает число рёбер. Этот процесс использует расширение заданного графа , а затем преобразование расширенного графа путём замены всех оригинальных вершин графа парой новых вершин. Этот “расщеплённый граф” является графом перестановок со специальными свойствами в том и только в том случае, когда является трапецеидальным.[7]
Замечания
- ↑ Ido Dagan, Martin Charles Golumbic, and Ron Yair Pinter. Trapezoid graphs and their coloring. Discrete Appl. Math., 35–46, 1988.
- ↑ Stefan Felsner, Rudolf Muller, and Lorenz Wernisch. Trapezoid graphs and generalizations, geometry and algorithms. In Algorithm theory—SWAT ’94 (Aarhus, 1994), volume 824 of Lecture Notes in Comput. Sci., pages 143–154. Springer, Berlin, 1994.
- ↑ Kenneth P. Bogart, Garth Isaak. Proper and unit bitolerance orders and graphs. Discrete Mathematics 181(1–3): 37–51 (1998).
- ↑ Martin Charles Golumbic and Irith B.-A. Hartman, eds., Graph Theory, Combinatorics and Algorithms: Interdisciplinary Applications, Springer-Verlag, New York, 2005
- ↑ R. McConnel and J. Spinrad, Linear-time modular decomposition and efficient transitive orientation of undirected graphs, Proc. 5. Ann. Symp. on Discr. Alg. (1994).
- ↑ Golumbic, Martin Charles., and Ann N. Trenk. Tolerance Graphs. Cambridge [u.a.: Cambridge Univ., 2004.
- ↑ G. B. Mertzios and D. G. Corneil. Vertex splitting and the recognition of trapezoid graphs. Discrete Applied Mathematics, 159(11), pages 1131-1147, 2011.
Ссылки
- Martin Charles Golumbic. Algorithmic Graph Theory and Perfect Graphs. — Academic Press, 1980. Second edition, Annals of Discrete Mathematics 57, Elsevier, 2004.