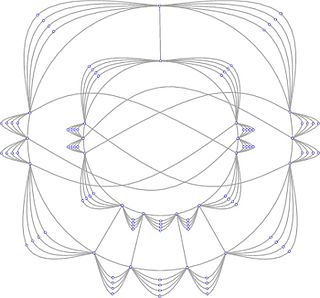
Трекл

Перейти к навигацииПерейти к поиску

Трекл — вложение графа в плоскость таким образом, что каждое ребро является кривой Жордана и каждая пара рёбер пересекается равно раз. Рёбра могут пересекаться по общей вершине, либо, если они не имеют общих вершин, во внутренних точках. В последнем случае предполагается, что пересечение трансверсально[1].

Линейные треклы

Линейный трекл — трекл, нарисованный прямолинейными отрезками. Любой линейный трекл имеет не больше рёбер, чем вершин, что обнаружил Пал Эрдёш. Эрдёш заметил, что если вершина v соединена с тремя и более рёбрами vw, vx и vy в линейном трекле, то по меньшей мере одно из этих рёбер лежит на прямой, разделяющей два других ребра. Без потери общности предположим, что таким ребром является vw, и точки x и y лежат по разные стороны замкнутых полупространств, ограниченных прямой vw. Тогда вершина w должна иметь степень единица, поскольку никакое другое ребро, отличное от vw, не может иметь общих точек как с vx, так и с vy. Удаление w из трекла даёт меньший трекл без изменения разности числа рёбер и вершин. С другой стороны, если любая вершина имеет максимум два соседа, то по лемме о рукопожатиях число рёбер не превосходит числа вершин[2]. Основываясь на доказательстве Эрдёша, можно сделать вывод, что любой линейный трекл является псевдолесом. Любой цикл нечётной длины можно преобразовать к линейному треклу, но это невозможно для циклов чётной длины, поскольку, если выбрать произвольное ребро, то другие вершины должны лежать поочерёдно по разные стороны от этого ребра.

Миша Перлес (Micha Perles) привёл другое простое доказательство, что линейный трекл имеет максимум n рёбер, основываясь на факте, что в линейном трекле любое ребро имеет конечную вершину, в которой все рёбра лежат внутри угла, не превосходящего 180°, для которого данное ребро является начальным (если смотреть по часовой стрелке). Если это не так, должны быть два ребра, инцидентных противоположным конечным вершинам ребра и лежащих по разные стороны от прямой, на котором ребро лежит. Эти рёбра друг друга не пересекают, но это возможно только для рёбер, смежных одной вершине[3].

Эрдёш также заметил, что множество пар точек, на которых достигается диаметр множества точек, должно представлять собой линейный трекл — никакие два диаметра не могут не иметь общих точек, поскольку среди четырёх концов этих диаметров две точки тогда должны лежать на расстоянии, большем диаметра. По этой причине любое множество из n точек на плоскости может иметь максимум n диаметральных пар, что отвечает на вопрос, поставленный в 1934 году Хайнцем Хопфом и Эрикой Панвиц[англ.] [4]. Эндрю Вашони[англ.] высказал гипотезу о границах числа диаметральных пар в более высоких размерностях, обобщив проблему[2].

В вычислительной геометрия может быть использован вращающийся кронциркуль[англ.]для получения линейного трекла из любого множества точек в выпуклой позиции[англ.] путём соединения пар точек, на которые опираются параллельные прямые, касающиеся выпуклой оболочки точек. Этот граф содержит в качестве подграфа трекл диаметральных точек[5]. Перечисление линейных треклов может быть использовано для решения задачи о наибольшем многоугольнике единичного диаметра, то есть задачи поиска n-угольника максимальной площади относительно его диаметра[6].

Гипотеза о трекле

Нерешённые проблемы математики: Может ли трекл иметь больше рёбер, чем вершин?
Вложение 6-цикла в виде трекла.

Джон Конвей высказал гипотезу, что в любом трекле число рёбер не превосходит числа вершин.

Эквивалентно, гипотезу можно переформулировать как любой трекл является псевдолесом. То есть, если гипотеза о трекле верна, принадлежность треклам может быть в точности выражена результатом Вудала — это псевдолеса, в которых нет циклов длины 4 и имеется по меньшей мере один нечётный цикл[1][7].

Было доказано, что любой циклический граф, отличный от C4, имеет вложение в виде трекла, что показывает, что гипотеза строга в том смысле, что имеются треклы, в которых число вершин равно числу рёбер. Другой крайний случай, когда число вершин вдвое больше числа рёбер, также достижим.

Известно, что гипотеза верна для треклов, нарисованных таким образом, что любое ребро является x-монотонной кривой, которая пересекается максимум один раз любой вертикальной линией[3].

Оценки

Ловас, Пач и Сегеди[8] доказали, что любой двудольный трекл является планарным графом, хотя он и не нарисован в планарном виде[1]. Как следствие, они показали, что любой тредставимый в виде трекла граф с n вершинами имеет максимум 2n − 3 рёбер. С тех пор граница была улучшена дважды. Сначала она была улучшена до 3(n − 1)/2[9], а последняя известная граница составляет около 1,428n[10]. Более того, метод, используемый для получения результата, даёт для любого ε > 0 конечный алгоритм, который либо улучшает границу до (1 + ε)n, либо опровергает гипотезу.

Известно, что если гипотеза неверна, минимальным контрпримером была бы пара чётных цикла с общей вершиной[7]. Таким образом, для доказательства гипотезы достаточно доказать, что графы этого типа нельзя нарисовать в виде треклов.

Примечания

  1. ↑ 1 2 3 Lovász, Pach, Szegedy, 1997, с. 369–376.
  2. ↑ 1 2 Erdős, 1946, с. 248–250.
  3. ↑ 1 2 Pach, Sterling, 2011, с. 544–548.
  4. ↑ Hopf, Pannwitz, 1934, с. 114.
  5. ↑ Toussaint, 2014, с. 372–386.
  6. ↑ Graham, 1975, с. 165–170.
  7. ↑ 1 2 Woodall, 1969, с. 335–348.
  8. ↑ Lovász, Pach, Szegedy, 1997.
  9. ↑ Cairns, Nikolayevsky, 2000, с. 191–206.
  10. ↑ Fulek, Pach, 2011, с. 345–355.

Литература

  • Уинклер П. Математические головоломки. Коллекция гурмана. — МЦНМО, 2024. — 176 с. — ISBN 978-5-4439-1819-8.
  • L. Lovász, J. Pach, M. Szegedy[англ.]. On Conway's thrackle conjecture // Discrete and Computational Geometry. — 1997. — Т. 18, вып. 4. — С. 369–376. — doi:10.1007/PL00009322. Предварительная версия этих результатов обсуждена в статье
    • J. O'Rourke[англ.]. Computational geometry column 26 // ACM SIGACT News. — 1995. — Т. 26, вып. 2. — С. 15–17. — doi:10.1145/202840.202842.
  • D. R. Woodall. Combinatorial Mathematics and Its Applications / D. J. A. Welsh. — Academic Press, 1969. — С. 335–348.
  • P. Erdős. On sets of distances of n points // American Mathematical Monthly. — 1946. — Т. 53. — С. 248–250. — doi:10.2307/2305092.
  • R. L. Graham. The largest small hexagon // Journal of Combinatorial Theory. — 1975. — Т. 18. — С. 165–170. — doi:10.1016/0097-3165(75)90004-7.
  • H. Hopf, E. Pannwitz[англ.]. Aufgabe Nr. 167 // Jahresbericht der Deutschen Mathematiker-Vereinigung. — 1934. — Т. 43. — С. 114.
  • Godfried Toussaint[англ.]. Applications of the rotating calipers to geometric problems in two and three dimensions // International Journal of Digital Information and Wireless Communications. — 2014. — Т. 4, вып. 3. — С. 372–386.
  • János Pach, Ethan Sterling. Conway's conjecture for monotone thrackles // American Mathematical Monthly. — 2011. — Т. 118, вып. 6. — С. 544–548. — doi:10.4169/amer.math.monthly.118.06.544.
  • G. Cairns, Y. Nikolayevsky. Bounds for generalized thrackles // Discrete and Computational Geometry. — 2000. — Т. 23, вып. 2. — С. 191–206. — doi:10.1007/PL00009495.
  • R. Fulek, J. Pach. A computational approach to Conway's thrackle conjecture // Computational Geometry. — 2011. — Т. 44, вып. 6-7. — С. 345–355. — doi:10.1007/978-3-642-18469-7_21.

Ссылки

  • thrackle.org — веб-сайт, посвящённый треклам