Треугольная квантовая яма

Треуго́льная ква́нтовая я́ма — одномерная потенциальная яма, ограниченная с одной стороны бесконечно высокой потенциальной стенкой, а с другой — потенциалом, линейно растущим с увеличением координаты. Один из простых профилей потенциала в квантовой механике, допускающих точное решение задачи о нахождении уровней энергии и волновых функций находящейся в яме частицы. Модель треугольной ямы используется, в частности, при исследованиях систем с двумерным электронным газом.

Одномерная треугольная потенциальная яма ограничена с одной стороны бесконечно высокой потенциальной стенкой (${\displaystyle U(x)\rightarrow +\infty }$ при ${\displaystyle -\infty <x\leqslant 0}$), а с другой — линейно растущим наклонным потенциалом ${\displaystyle 0<U\left(x\right)=Fx<+\infty }$ при ${\displaystyle 0<x<+\infty }$ (см. рис.1)^[1]. Такой вид потенциальной энергии ${\displaystyle U(x)}$ соответствует однородному полю, действующему на частицу с силой ${\displaystyle -F=dU/dx}$, не зависящей от координаты^[2]. Примерами таких полей являются однородное электрическое поле ${\displaystyle U\left(x\right)=qE_{el}x\geq 0}$ (${\displaystyle q}$ — заряд частицы, ${\displaystyle E_{el}}$ — напряженность электрического поля)^[3] и гравитационное поле тяжести ${\displaystyle U\left(x\right)=mgx}$ (${\displaystyle m}$ — масса частицы, ${\displaystyle g}$ —ускорение свободного падения)^[4].

Уравнение Шрёдингера для частицы в однородном поле имеет вид^[1][4][5]:

${\displaystyle {\frac {d^{2}\psi }{dx^{2}}}+{\frac {2m}{\hbar \;^{2}}}(E-Fx)\psi =0\,.}$

Граничные условия описывают абсолютно упругое отражение от потенциальной стенки при ${\displaystyle x=0}$^[4] и убывание решения в классически недоступной области ${\displaystyle Fx>E}$ при ${\displaystyle x\rightarrow +\infty }$^[1]:

${\displaystyle \psi (x=0)=0,\qquad \psi (x\rightarrow +\infty )\rightarrow 0\,.}$

Здесь ${\displaystyle m}$ — масса частицы, ${\displaystyle \hbar }$ — редуцированная постоянная Планка, ${\displaystyle E}$ и ${\displaystyle \psi }$ — искомые энергия и волновая функция частицы.

Для упрощения дальнейшего рассмотрения вводится безразмерная переменная^[2]

${\displaystyle \xi =\alpha \left(x-{\frac {E}{F}}\right)\,,}$

где ${\displaystyle \alpha =\left({\frac {2mF}{\hbar \;^{2}}}\right)^{1/3}}$. При использовании новой переменной задача сводится к решению уравнения Эйри

${\displaystyle \psi ''(\xi )-\xi \psi (\xi )=0\,}$

с граничными условиями

${\displaystyle \psi \left(-\alpha {\frac {E}{F}}\right)=0,\quad \psi (\xi \rightarrow +\infty )\rightarrow 0\,.}$

Общее решение уравнения Эйри имеет вид^[6]:

${\displaystyle \psi (\xi )=C\mathrm {Ai} (\xi )+D\mathrm {Bi} (\xi )\,,}$

где ${\displaystyle \mathrm {Ai} }$ и ${\displaystyle \mathrm {Bi} }$ — функции Эйри 1-го и 2-го рода имеют при больших ${\displaystyle \xi \rightarrow +\infty }$ следующие асимптотики^[7]

${\displaystyle {\begin{aligned}\mathrm {Ai} \,(\xi )&{}\sim {\frac {e^{-{\frac {2}{3}}\xi ^{3/2}}}{2{\sqrt {\pi }}\,\xi ^{1/4}}}\,,\\\mathrm {Bi} \,(\xi )&{}\sim {\frac {e^{{\frac {2}{3}}\xi ^{3/2}}}{{\sqrt {\pi }}\,\xi ^{1/4}}}\,.\end{aligned}}}$

При отрицательных значениях ${\displaystyle \xi }$ функции Эйри осциллируют и имеют бесконечное число нулей. Из граничного условия на бесконечности ${\displaystyle \xi \rightarrow +\infty }$ и экспоненциального роста ${\displaystyle \mathrm {Bi} (\xi \rightarrow +\infty )}$ следует, что константа ${\displaystyle D=0}$ , то есть решение задачи следует искать в виде^[4]

${\displaystyle \psi (\xi )=C\mathrm {Ai} (\xi )\,.}$

Собственные значения энергии частицы ${\displaystyle E=E_{n}}$ (${\displaystyle n=1,\,\,2,..}$) в треугольной яме определяются из условия обращения в нуль волновой функции на границе бесконечной потенциальной стенки^[4]:

${\displaystyle \psi _{n}\left(\xi _{n}=-\alpha {\frac {E_{n}}{F}}\right)=C_{n}\mathrm {Ai} \left(-\alpha {\frac {E_{n}}{F}}\right)=0\,,}$

где ${\displaystyle \xi _{n}=-a_{n}}$ — нули функции Эйри. В результате находим дискретный спектр энергий^[1],

${\displaystyle E_{n}={\frac {Fa_{n}}{\alpha }}={\frac {\hbar ^{2}\alpha ^{2}a_{n}}{2m}}\,,}$

а соответствующая дискретному уровню ${\displaystyle E_{n}}$волновая функция имеет вид:

${\displaystyle {{\psi }_{n}}\left(x\right)=C_{n}\mathrm {Ai} \left(\alpha x-{{a}_{n}}\right)\,.}$

Для первых пяти нулей значения ${\displaystyle a_{n}}$ приближённо равны: ${\displaystyle a_{1}=2,338}$, ${\displaystyle a_{2}=4,088}$, ${\displaystyle a_{3}=5,521}$, ${\displaystyle a_{4}=6,787}$, ${\displaystyle a_{5}=7,944}$^[4]. При больших ${\displaystyle n\gg 1}$ нули функций Эйри определяются выражением^[8]:

${\displaystyle a_{n}\approx \left[{\frac {3\pi }{2}}\,\left(n-{\frac {1}{4}}\right)\right]^{2/3}\,.}$

Значения констант ${\displaystyle C_{n}}$ находятся из условия нормировки^[9]

${\displaystyle \int \limits _{0}^{\infty }{dx}{{\left|\psi _{n}\left(x\right)\right|}^{2}}=1\,.}$

Вычисляя интеграл от квадрата волновой функции, которая вещественна^[10],

${\displaystyle {\begin{aligned}&C_{n}^{2}{{\alpha }^{-1}}\int \limits _{-{{a}_{n}}}^{\infty }{d\xi }\mathrm {Ai} ^{2}\left(\xi \right)=\\&C_{n}^{2}{{\alpha }^{-1}}\left[\xi \mathrm {Ai} ^{2}\left(\xi \right)-{{\left(\mathrm {Ai} '\left(\xi \right)\right)}^{2}}\right]_{\xi =-{{a}_{n}}}^{\infty }=\\&C_{n}^{2}{{\alpha }^{-1}}{{\left(\mathrm {Ai} '\left(-{{a}_{n}}\right)\right)}^{2}}=1,\\\end{aligned}}}$

находим нормировочные константы, которые зависят от номера квантового уровня:

${\displaystyle {{C}_{n}}={\frac {{\alpha }^{1/2}}{\mathrm {Ai} '\left(-{{a}_{n}}\right)}}\,,}$

где ${\displaystyle \mathrm {Ai} '(\xi )}$ — производная функции Эйри.

Функции ${\displaystyle \psi _{n}(x)}$ ортогональны. В этом можно убедиться, вычислив интеграл от произведения волновых функций, принадлежащих разным квантовым состояниям ${\displaystyle n\neq m}$^[11]:

${\displaystyle {\begin{aligned}&{{C}_{n}}{{C}_{m}}\int \limits _{0}^{\infty }{dx}\mathrm {Ai} \left(\alpha x-{{a}_{n}}\right)\mathrm {Ai} \left(\alpha x-{{a}_{m}}\right)=\\&{\frac {{{C}_{n}}{{C}_{m}}}{\alpha \left({{a}_{m}}-{{a}_{n}}\right)}}\left[\mathrm {Ai} '\left(\alpha x-{{a}_{n}}\right)\mathrm {Ai} \left(\alpha x-{{a}_{m}}\right)-\right.\\&\left.\mathrm {Ai} \left(\alpha x-{{a}_{n}}\right)\mathrm {Ai} '\left(\alpha x-{{a}_{m}}\right)\right]_{x=0}^{\infty }=0.\\\end{aligned}}}$

Для рассматриваемой ямы волновые функции экспоненциально убывают ${\displaystyle \mathrm {Ai} \left(\alpha x-a_{n}\right)\sim {{x}^{-1/4}}\exp \left(-2{{(\alpha x)}^{3/2}}/3\right)}$ при ${\displaystyle x\rightarrow +\infty }$ и отличны от нуля при сколь угодно больших расстояниях ${\displaystyle x}$. Ширина классически доступной (${\displaystyle E_{n}>U(x)}$) области находится из условия

${\displaystyle U(x_{n})=Fx_{n}=E_{n}}$

и составляет^[4]

${\displaystyle x_{n}={\frac {a_{n}}{\alpha }}.}$

Значения ${\displaystyle x_{n}}$ схематически показаны на рисунке 1.

Задача об энергетическом спектре магнитных поверхностных уровней электронов приближённо сводится к модели треугольной потенциальной ямы. На малых расстояниях от поверхности проводника и в слабом магнитном поле в уравнении Шрёдингера можно пренебречь слагаемыми, квадратичными по векторному потенциалу, и эффективный потенциал ямы линейно зависит от расстояния от поверхности, которая описывается бесконечной стенкой^[12].

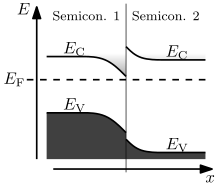
Модель треугольной ямы используется при исследованиях двумерного электронного газа в инверсных слоях у границ раздела диэлектрик—полупроводник и границ двух разных полупроводников. Хотя в таких системах профиль зоны проводимости в полупроводнике сложнее, чем линейный, а разрыв зоны проводимости на гетерогранице не является бесконечным (см. рис.2), непосредственно вблизи этой границы яма приближённо считается треугольной, а разрыв зоны достаточно большим^[13].

• Квантовое движение в электрическом поле
• Прямоугольная квантовая яма
• Осцилляции Зенера — Блоха
• Квантовый осциллятор
• Магнитные поверхностные уровни

• Ландау Л. Д., Лифшиц Е. М. Квантовая механика. Нерелятивистская теория (рус.). — Москва: Наука, 1989. — С. 112. — 768 с. — ISBN 5-02-014421-5.
• Olivier Vallee, Manuel Soares. Airy functions and applications to physics (англ.). — London: Imperial College Press, 2004. — 194 p. — ISBN 1-86094-478-7.