
Пло́щадь — в узком смысле, площадь фигуры — численная характеристика, вводимая для определённого класса плоских геометрических фигур и обладающая свойствами площади. Интуитивно, из этих свойств следует, что бо́льшая площадь фигуры соответствует её «большему размеру», a оценить площадь фигуры можно с помощью наложения на её рисунок сетки из линий, образующих одинаковые квадратики и подсчитав число квадратиков и их долей, попавших внутрь фигуры. В широком смысле понятие площади обобщается на k-мерные поверхности в n-мерном пространстве, в частности, на двумерную поверхность в трёхмерном пространстве.

Теорема Бойяи — Гервина утверждает, что любые два равновеликих многоугольника равносоставлены.
Пери́метр — общая длина границы фигуры. Имеет ту же размерность величин, что и длина.
Теорема о сумме углов многоугольника выражает сумму углов евклидова многоугольника через число его сторон.
Интегральное исчисление — раздел математического анализа, в котором изучаются понятия интеграла, его свойства и методы вычислений.

Диаграмма Вороного конечного множества точек S на плоскости представляет такое разбиение плоскости, при котором каждая область этого разбиения образует множество точек, более близких к одному из элементов множества S, чем к любому другому элементу множества.
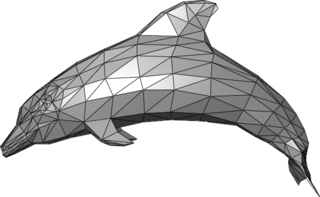
Полигональная сетка — это совокупность вершин, рёбер и граней, которые определяют форму многогранного объекта в трёхмерной компьютерной графике и объёмном моделировании. Гранями обычно являются треугольники, четырёхугольники или другие простые выпуклые многоугольники (полигоны), так как это упрощает рендеринг, но сетки могут также состоять и из наиболее общих вогнутых многоугольников[прояснить], или многоугольников с отверстиями.

Триангуля́ция Делоне́ — триангуляция для заданного множества точек S на плоскости, при которой для любого треугольника все точки из S за исключением точек, являющихся его вершинами, лежат вне окружности, описанной вокруг треугольника. Обозначается DT(S). Впервые описана в 1934 году советским математиком Борисом Делоне.

Триангуляция — один из методов создания сети опорных геодезических пунктов, а также сама эта сеть.

Триангуляция — разбиение геометрического объекта на симплексы. Например, на плоскости это разбиение на треугольники, откуда и происходит это название.
Геодезическая сеть — сеть специально обозначенных точек земной поверхности, положение которых определено в общей для них системе геодезических координат. Разделяются на плановые, высотные и планово-высотные.

Парке́т или замощение — разбиение плоскости на многоугольники или пространства на многогранники без пробелов и наслоений.

Семиугольная мозаика — правильная мозаика на гиперболической плоскости. Она представляется cимволом Шлефли {7,3} и имеет три правильных семиугольника в каждой вершине.

Многогранник Шёнхардта — простейший невыпуклый многогранник, который нельзя триангулировать тетраэдрами без добавления новых вершин. Многогранник назван именем немецкого математика Эриха Шёнхардта, построившего его в 1928 году.

Задача о триангуляции многоугольника — классическая задача комбинаторной и вычислительной геометрии, состоящая в нахождении триангуляции многоугольника без дополнительных вершин.
Задача Вебера — одна из наиболее известных задач размещения производства. Названна в честь немецкого экономиста Альфреда Вебера. В задаче требуется найти точку на плоскости, которая минимизирует сумму цен перевозок из этой точки в n точек потребления, где для разных точек потребления назначается своя цена перевозки на единицу расстояния.

Простой многоугольник — это фигура, состоящая из непересекающихся отрезков («сторон»), соединённых попарно с образованием замкнутого пути. Если стороны пересекаются, многоугольник не является простым. Часто слово «простой» опускается из вышеприведённого определения.
Разбиение многоугольника — это множество примитивных элементов, которые не накладываются и объединение которых равно многоугольнику. Задача о разбиении многоугольника — это задача поиска разбиения, которое в некотором смысле минимально, например, разбиение с наименьшим числом элементов или разбиение с наименьшей суммой длин сторон.
Причинная динамическая триангуляция (ПДТ) — разновидность теории квантовой гравитации, основанная на математической гипотезе о двумерной структуре пространства-времени и его фрактальной структуре на сечениях постоянного времени при расстояниях порядка планковской длины и интервалах времени порядка планковского времени.














