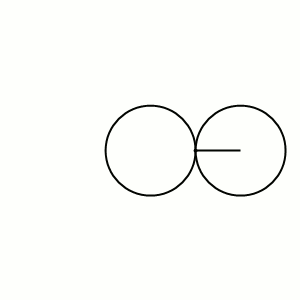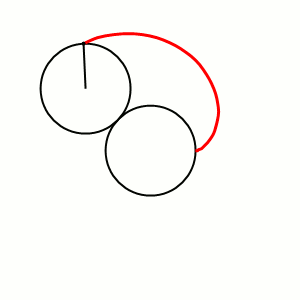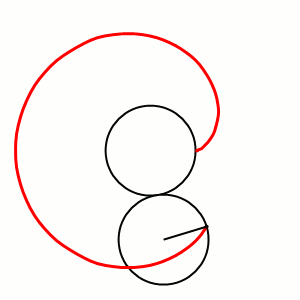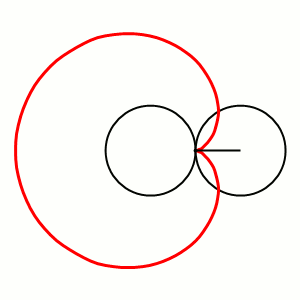Крива́я или ли́ния — геометрическое понятие, определяемое в разных разделах математики различно.
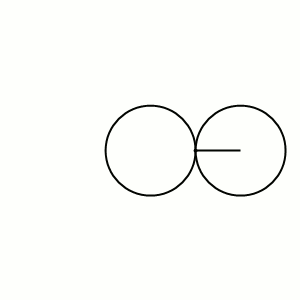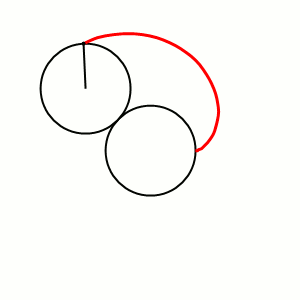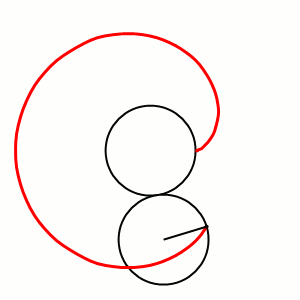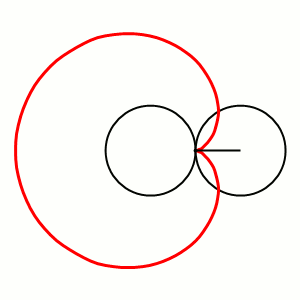
Кардио́ида, или сердцеви́дная крива́я — плоская линия, которая описывается фиксированной точкой окружности, катящейся по неподвижной окружности с таким же радиусом. Получила своё название из-за схожести своих очертаний со стилизованным изображением сердца.
Трактри́са — — плоская трансцендентная кривая, для которой длина отрезка касательной от точки касания до точки пересечения с фиксированной прямой является постоянной величиной. Такую линию описывает предмет, волочащийся на верёвке длины a за точкой, движущейся по оси абсцисс. Трактриса также является кривой погони.
Эпицикло́ида — плоская кривая, образуемая фиксированной точкой окружности, катящейся по внешней стороне другой окружности без скольжения.
Эпитрохо́ида — плоская кривая, образуемая точкой, жёстко связанной с окружностью, катящейся по внешней стороне другой окружности.
Цикло́ида — плоская трансцендентная кривая.
Кривизна́ — собирательное название ряда характеристик, описывающих отклонение того или иного геометрического «объекта» от соответствующих «плоских» объектов.
Синусо́ида — плоская кривая, задаваемая в прямоугольных координатах уравнением
Эволю́та плоской кривой — геометрическое место точек, являющихся центрами кривизны исходной кривой.
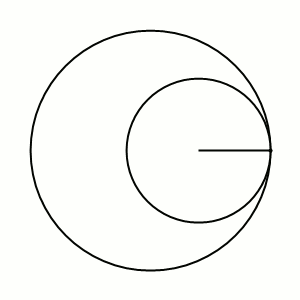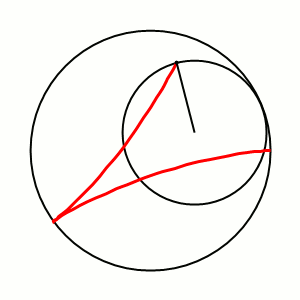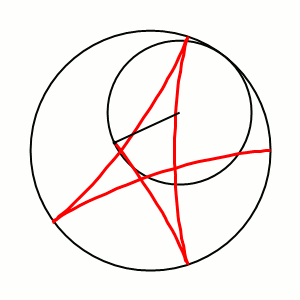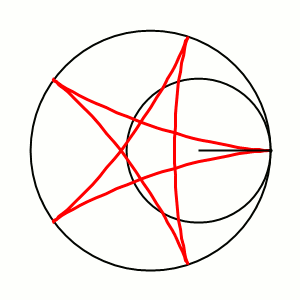
Гипоцикло́ида — плоская кривая, образуемая точкой окружности, катящейся по внутренней стороне другой окружности без скольжения.
Винтовая ли́ния — кривая в трёхмерном пространстве, расположенная на круглом цилиндре или круглом конусе и пересекающая образующие под одинаковым углом.
Гиперболическая спираль — плоская трансцендентная кривая. Уравнение гиперболической спирали в полярной системе координат является обратным для уравнения Архимедовой спирали и записывается так:
Квадратри́са — плоская трансцендентная кривая, определяемая кинематически. Была предложена в античные времена для решения задач квадратуры круга и трисекции угла. Квадратриса стала первой в математике трансцендентной кривой.
Нефро́ида — плоская алгебраическая кривая 6-го порядка, которую описывает фиксированная точка окружности, катящейся снаружи по большей в два раза окружности. Является частным случаем эпициклоиды при 
. Названа так от др.-греч. νεφρός — «почка» и εἶδος — «вид, фигура» из-за своей формы, напоминающей почки.
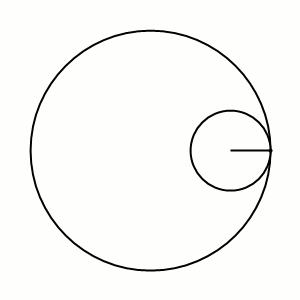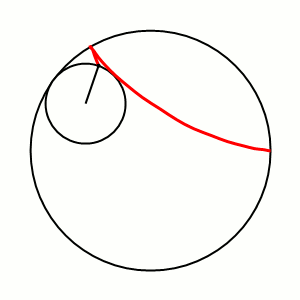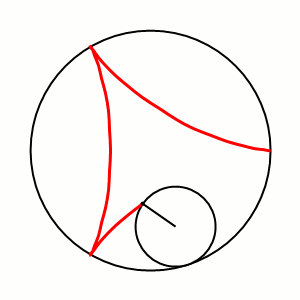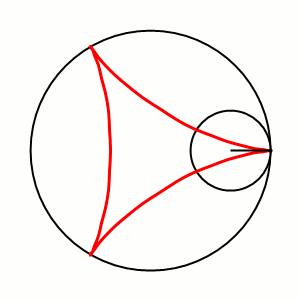
Дельтоида — плоская алгебраическая кривая, описываемая фиксированной точкой окружности, катящейся по внутренней стороне другой окружности, радиус которой втрое больше радиуса первой.
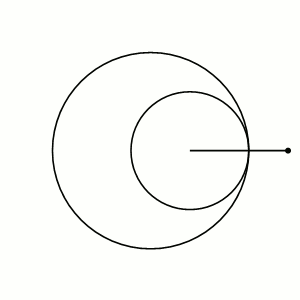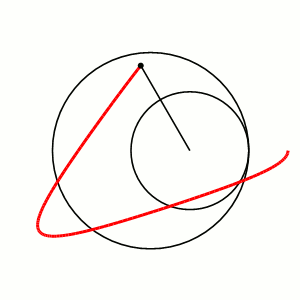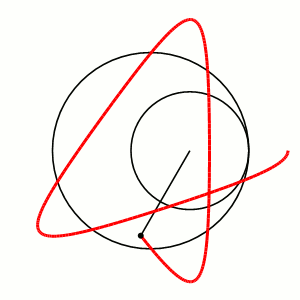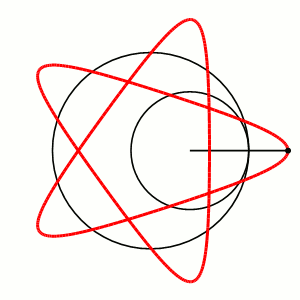
Гипотрохоида — плоская кривая, образуемая фиксированной точкой, находящейся на фиксированной радиальной прямой окружности, катящейся по внутренней стороне другой окружности.
Квазитрохоида — — плоская трансцендентная кривая, по форме напоминающая трохоиду, но отличающаяся тем, что центр вращения перемещается по произвольной траектории, радиус и частота вращения могут изменяться во времени по любому закону.
Циклоидальная кривая — плоская кривая, рисуемая точкой, находящейся на радиальной прямой окружности, катящейся по какой-либо кривой. Название происходит от греческого κυκλοειδής — «круглый».
Инверсия кривой — результат применения операции инверсии к заданной кривой C. По отношению к фиксированной окружности с центром O и радиусом k инверсия точки Q — это точка P, лежащая на луче OQ, и OP•OQ = k2. Инверсия кривой C — это множество всех точек P, являющихся инверсиями точек Q, принадлежащих кривой C. Точка O в этом построении называется центром инверсии, окружность называется окружностью инверсии, а k — радиусом инверсии.
