Замечательные точки треугольника — точки, местоположение которых однозначно определяется треугольником и не зависит от того, в каком порядке берутся стороны и вершины треугольника.
В теории графов графом без треугольников называется неориентированный граф, в котором никакие три вершины не образуют треугольник из рёбер. Графы без треугольников можно определить также как графы с кликовым числом ≤ 2, графы с обхватом ≥ 4, графы без порождённых 3-циклов, или как локально независимые графы.
Гипотеза Визинга — предположение о связи доминирующего множества и прямого произведения графов, не подтверждённое по состоянию на 2017 год, при этом гипотеза доказана для ряда частных случаев.

Жадная раскраска в теории графов — раскраска вершин неориентированного графа, созданная жадным алгоритмом, который проходит вершины графа в некоторой предопределённой последовательности и назначает каждой вершине первый доступный цвет. Жадные алгоритмы, в общем случае, не дают минимально возможное число цветов, однако они используются в математике в качестве техники доказательств других результатов, относящихся к раскраске, а также в компьютерных программах для получения раскраски с небольшим числом цветов.

Центр Шпикера — замечательная точка треугольника, определяемая как центр масс периметра треугольника; то есть центр тяжести однородной проволоки, проходящей по периметру треугольника.

Теорема об упаковке кругов описывает возможные варианты касания окружностей, не имеющих общих внутренних точек. Граф пересечений упаковки кругов — это граф, вершины которого соответствуют кругам, а рёбра — точкам касания. Если упаковка кругов осуществляется на плоскости, то их граф пересечений называется графом монет. Графы монет всегда связны, просты и планарны. Теорема упаковки кругов утверждает, что обратное также верно:

Окружности Мальфатти — три окружности внутри заданного треугольника, такие, что каждая окружность касается двух других и двух сторон треугольника. Окружности названы именем Джанфранческо Мальфатти, который начал исследовать задачу построения этих окружностей с ошибочным убеждением, что они в сумме дают максимальную возможную площадь трёх непересекающихся окружностей внутри треугольника. Задача Мальфатти относится к обеим задачам — как к построению окружностей Мальфатти, так и к задаче нахождения трёх непересекающихся окружностей внутри треугольника с максимальной общей площадью.

Конфигура́ция прямы́х — это разбиение плоскости, образованное набором прямых. Конфигурации прямых изучается в комбинаторной геометрии, а в вычислительной геометрии строятся алгоритмы для эффективного построения конфигураций.

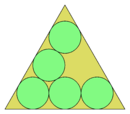
В геометрии упаковка кругов — это изучение размещения кругов на заданной поверхности таким образом, что они не пересекаются и круги касаются друг друга. Соответствующая плотность упаковки η размещения — это доля занятой кругами поверхности. Можно обобщить упаковки кругов на более высокие размерности — она называется упаковкой шаров, которая, обычно, работает с одинаковыми сферами.
Упаковка кругов в круге — это двумерная задача упаковки, целью которой является упаковка единичных кругов в как можно меньший круг.
Задачи упаковки — это класс задач оптимизации в математике, в которых пытаются упаковать объекты в контейнеры. Цель упаковки — либо упаковать отдельный контейнер как можно плотнее, либо упаковать все объекты, использовав как можно меньше контейнеров. Многие из таких задач могут относиться к упаковке предметов в реальной жизни, вопросам складирования и транспортировки. Каждая задача упаковки имеет двойственную задачу о покрытии, в которой спрашивается, как много требуется некоторых предметов, чтобы полностью покрыть все области контейнера, при этом предметы могут накладываться.
В теории графов вполне упорядочиваемый граф — это граф, вершины которого можно упорядочить так, что алгоритм жадной раскраски с этим упорядочением оптимально раскрашивает любой порождённый подграф заданного графа. Соответствующее упорядочение называется совершенным. Вполне упорядочиваемые графы образуют подкласс совершенных графов и в это подкласс входят хордальные графы, графы сравнимости и дистанционно-наследуемые графы. Однако проверка, является ли граф вполне упорядочиваемым, есть NP-полная задача.

В теории графов круговой граф — это граф пересечений множества хорд окружности. То есть это неориентированный граф, вершины которого можно отождествить с хордами окружности, и эти вершины смежны тогда и только тогда, когда соответствующие хорды пересекаются.
Однозначно раскрашиваемый граф — это k-цветный граф, допускающий только одну (правильную) k-раскраску.

Упаковка тетраэдров — это задача расположения одинаковых правильных тетраэдров в трёхмерном пространстве так, чтобы заполнить как можно большую долю пространства.
Индифферентный граф — это неориентированный граф, построенный путём назначения вещественного числа каждой вершине и соединения двух вершин ребром, когда их числа отличаются не более чем на единицу. Индифферентные графы являются также графами пересечений множеств единичных отрезков или интервалов с определённым свойством вложения. Основываясь на этих двух типах интервальных представлений, эти графы называются также графами единичных отрезков или собственными интервальными графами. Индифферентные графы образуют подкласс интервальных графов.
Треугольник Белла — это треугольник чисел, аналогичный треугольнику Паскаля, значения которого содержат число разбиений множества, в которых заданный элемент является наибольшим синглтоном. Треугольник назван по тесной связи с числами Белла, которые можно найти с обеих сторон треугольника,. Треугольник Белла был неоднократно открыт независимо несколькими авторами, начиная с Чарльза Сандерса Пирса и включая Александра Айткена и группу авторов — Кона, Ивена, Менгера и Хупера. По этой причине треугольник называется также массивом Айткена или треугольником Пирса
Гипотеза Шейнермана, теперь доказанная теорема, утверждает, что любой планарный граф является графом пересечений набора отрезков на плоскости. Эту гипотезу сформулировал Эдвард Шейнерман в своей кандидатской диссертации, следуя более раннему результату, что любой планарный граф можно представить как граф пересечений простых кривых на плоскости. Теорему доказали Чалопин и Гонсалвис.
Выигрышный граф полицейского — это неориентированный граф, на котором преследователь (полицейский) может выиграть игру преследования-уклонения, в которой он преследует грабителя и игроки поочерёдно делают передвижения вдоль рёбер графа или стоят на месте пока, полицейский не займёт вершину, на которой находится грабитель. Конечные выигрышные графы полицейского называются также разбираемыми графами или конструируемыми графами, поскольку они могут быть разобраны путём удаления раз за разом доминируемой вершины или построены путём повторяющегося добавления такой вершины. Выигрышные графы полицейского могут быть распознаны за полиномиальное время жадным алгоритмом, который создаёт порядок разборки. В этот класс входят хордальные графы и графы, содержащие универсальную вершину.
Упаковка квадратов в квадрате — одна из задач упаковки. Состоит в определении минимального размера квадратного контейнера в который умещается  единичных квадратов.
единичных квадратов.