Уравнение Чандрасекара

Уравне́ние Чандрасека́ра в астрофизике — безразмерная форма уравнения Пуассона для распределения плотности сферически-симметричной изотермической газовой сферы под действием собственной силы гравитации, названная по имени американского астрофизика Субраманьяна Чандрасекара.[1][2] Уравнение[3] имеет вид
где является безразмерным радиусом, связано с плотностью газовой сферы соотношением , где представляет плотность газа в центре. Уравнение не имеет известного явного решения. Если вместо изотермического вещества взять политропное, записанное уравнение будет представлять собой уравнение Лейна — Эмдена. Обычно изотермическое приближение применяется при описании ядра звезды. В таком случае уравнение решают с начальными условиями
Уравнение также возникает и в других областях физики, например, в разработанной Д. А. Франк-Каменецким теории теплового взрыва в замкнутой оболочке[англ.].
Вывод уравнения
Для изотермической газовой звезды давление складывается из кинетического давления и давления излучения:
- ,
где
- — плотность,
- — постоянная Больцмана,
- — средний молекулярный вес,
- — масса протона,
- — температура звезды,
- — постоянная Стефана — Больцмана,
- — скорость света.
Уравнение для состояния равновесия звезды требует баланса между силой давления и силой гравитации:
где равно радиусу, измеряемому от центра, является гравитационной постоянной. Уравнение переписывается в виде
Вводя преобразования
где — плотность звезды в центральной части, получаем выражение
Граничные условия таковы:
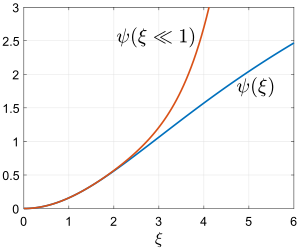
При решение близко к
Ограничения модели
Предположение об изотермичности сферы имеет некоторые недостатки. Хотя полученная при решении плотность изотермической газовой сферы уменьшается с удалением от центра, всё же уменьшение слишком медленное для того, чтобы получалась надёжно определяемая поверхность и масса сферы оказывалась конечной[4]. Можно показать, что при ,
- ,
где и являются постоянными величинами, которые можно получить при численном решении. Такое поведение плотности приводит к увеличению массы при возрастании радиуса. Следовательно, модель обычно пригодна для описания ядер звёзд, где температура приблизительно постоянна.
Особое решение
Преобразование приводит уравнение к виду
Уравнение имеет особое решение вида
Следовательно, можно ввести новую переменную при этом уравнение для можно вывести:
Данное уравнение можно свести к уравнению первого порядка, вводя переменную
тогда
Другие варианты уравнения
Уравнение можно привести к другому виду. Пусть
тогда
Свойства
- Если является решением уравнения Чандрасекара, то также является решением уравнения при произвольной константе .
- Решения уравнения Чандрасекара, являющиеся конечными в начале координат, удовлетворяют условию при .
Примечания
- ↑ Chandrasekhar, Subrahmanyan, and Subrahmanyan Chandrasekhar. An introduction to the study of stellar structure. Vol. 2. Courier Corporation, 1958.
- ↑ Chandrasekhar, S., and Gordon W. Wares. «The Isothermal Function.» The Astrophysical Journal 109 (1949): 551—554.http://articles.adsabs.harvard.edu/cgi-bin/nph-iarticle_query?1949ApJ...109..551C&defaultprint=YES&filetype=.pdf
- ↑ Kippenhahn, Rudolf, Alfred Weigert, and Achim Weiss. Stellar structure and evolution. Vol. 282. Berlin: Springer-Verlag, 1990.
- ↑ Poisson, Eric, and Clifford M. Will. Gravity: Newtonian, Post-Newtonian, Relativistic. Cambridge University Press, 2014.
























![{\displaystyle {\frac {\rho }{\rho _{c}}}=e^{-\psi }={\frac {2}{\xi ^{2}}}\left[1+{\frac {A}{\xi ^{1/2}}}\cos \left({\frac {\sqrt {7}}{2}}\ln \xi +\delta \right)+O(\xi ^{-1})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e8e7421b0c06fccfc3d41bd1ec453621216c727f)





















