Уравнение времени

Уравнение времени — разница между средним солнечным временем (ССВ) и истинным солнечным временем (ИСВ), то есть УВ = ССВ − ИСВ^[1]. Эта разница в каждый конкретный момент времени одинакова для наблюдателя в любой точке Земли. Уравнение времени можно узнать из специализированных астрономических изданий, астрономических программ или вычислить по формуле, приведённой ниже.

В таких изданиях, как «Астрономический календарь», уравнение времени определяется как разность часовых углов среднего экваториального солнца и истинного солнца, то есть при таком определении УВ = ССВ − ИСВ^[2].

В англоязычных изданиях часто применяется «инвертированное» определение уравнения времени: УВ = ИСВ − ССВ, то есть разница между истинным солнечным временем и средним солнечным временем.

Можно встретить определение уравнения времени как разницы «местного истинного солнечного времени» и «местного среднего солнечного времени» (в англоязычной литературе — local apparent solar time и local mean solar time). Данное определение формально более точно, но не влияет на результат, так как для любой конкретной точки на Земле эта разница одинакова.

Кроме того, не следует путать ни местное истинное, ни местное среднее солнечное время с официальным местным временем (standard time).

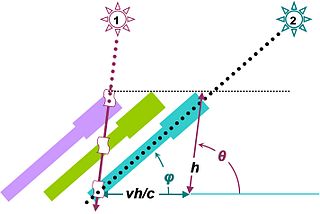
В отличие от звёзд, чьё видимое суточное движение практически равномерно и обусловлено только вращением Земли вокруг своей оси, суточное движение Солнца не равномерно, так как обусловлено и вращением Земли вокруг своей оси, и обращением Земли вокруг Солнца, и наклоном земной оси к плоскости орбиты Земли.

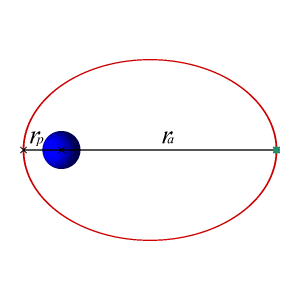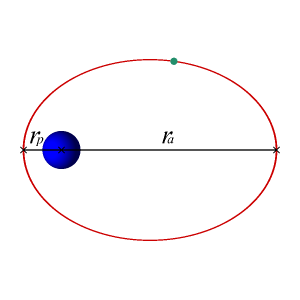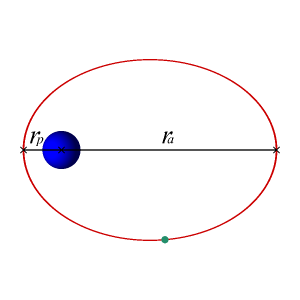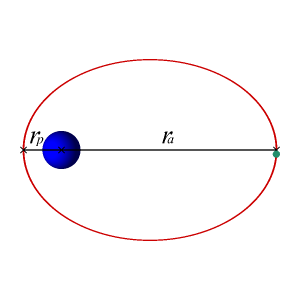
Вращение Земли вокруг Солнца происходит по эллиптической орбите. Согласно второму закону Кеплера, такое движение неравномерно, оно быстрее в области перигелия и медленнее в области афелия. Для наблюдателя, находящегося на Земле, это выражается в том, что видимое движение Солнца по эклиптике относительно неподвижных звёзд то ускоряется, то замедляется.

Поскольку плоскость эклиптики наклонена к плоскости небесного экватора, имеет место следующее явление:

• Солнце вблизи солнцестояний (зимнего и летнего) движется почти параллельно небесному экватору, и скорость его перемещения практически полностью вычитается из суточного движения небесной сферы — результирующая скорость изменения часового угла Солнца минимальна;
• Солнце вблизи равноденствий (осеннего и весеннего) движется под максимальным углом к небесному экватору, и скорость его перемещения лишь частично вычитается из суточного движения небесной сферы — результирующая скорость изменения часового угла Солнца максимальна.

Кривая уравнения времени является суммой двух периодических кривых — с периодами 1 год и 6 месяцев. Практически синусоидальная кривая с годичным периодом обусловлена неравномерным движением Солнца по эклиптике. Эта часть уравнения времени называется уравнением центра или уравнением от эксцентриситета. Синусоида с периодом 6 месяцев представляет разность времён, вызванную наклоном эклиптики к небесному экватору и называется уравнением от наклона эклиптики^[1].

Уравнение времени обращается в ноль четыре раза в году — приблизительно 15 апреля, 13 июня, 1 сентября и 25 декабря^[3].

Соответственно, в каждое время года существует свой максимум уравнения времени: около 12 февраля — +14,3 мин, 15 мая — −3,8 мин, 27 июля — +6,4 мин и 4 ноября — −16,4 мин. Точные величины уравнения времени даются в астрономических ежегодниках.

Может применяться как дополнительная функция в некоторых моделях часов.

Уравнение можно аппроксимировать отрезком ряда Фурье как сумму двух синусоидальных кривых с периодами, соответственно, один год и шесть месяцев:

${\displaystyle E=7.53\cos(B)+1.5\sin(B)-9.87\sin(2B)}$,

где

${\displaystyle B=360(N-81)/365}$, если углы выражаются в градусах,

или

${\displaystyle B=2\pi (N-81)/365}$, если углы выражаются в радианах.

Там, где ${\displaystyle N}$ — номер дня в году, например:

${\displaystyle N=1}$ на 1 января,

${\displaystyle N=2}$ на 2 января,

и так далее.

• Аналемма

• Величина колебаний уравнения времени в течение года на портале Гринвичской королевской обсерватории.
• Уравнение времени на сегодняшний день — визуализация.
• [bse.sci-lib.com/a_pictures/04/18/260109925.jpg Образец построения графика уравнения времени], где прорисованы:

1 — составляющая уравнения времени, определяемая неравномерностью движения Земли по орбите,

2 — составляющая уравнения времени, определяемая наклоном эклиптики к экватору,

3 — уравнение времени.