Ква́нтовая тео́рия по́ля (КТП) — раздел физики, изучающий поведение квантовых систем с бесконечно большим числом степеней свободы — квантовых полей; является теоретической основой описания микрочастиц, их взаимодействий и превращений. На языке КТП основываются физика высоких энергий и физика элементарных частиц, её математический аппарат используется в физике конденсированного состояния. КТП в виде Стандартной модели в настоящее время является единственной экспериментально подтверждённой теорией, способной описывать и предсказывать результаты экспериментов при достижимых в современных ускорителях высоких энергиях.

Волна́ — изменение некоторой совокупности физических величин, которое способно перемещаться, удаляясь от места их возникновения, или колебаться внутри ограниченных областей пространства.

Просветле́ние о́птики — технология обработки поверхности линз, призм и других оптических деталей для снижения отражения света от оптических поверхностей, граничащих с воздухом. Это позволяет увеличить светопропускание оптической системы и повысить контрастность изображения за счёт снижения мешающих паразитных отражений в оптической системе.

Интерфере́нция све́та — интерференция электромагнитных волн — перераспределение интенсивности света в результате наложения (суперпозиции) нескольких световых волн. Это явление обычно характеризуется чередующимися в пространстве максимумами и минимумами интенсивности света. Конкретный вид такого распределения интенсивности света в пространстве или на экране, куда падает свет, называется интерференционной картиной.

Интерференция волн — взаимное увеличение или уменьшение результирующей амплитуды двух или нескольких когерентных волн при их наложении друг на друга. Сопровождается чередованием максимумов (пучностей) и минимумов (узлов) интенсивности в пространстве. Результат интерференции зависит от разности фаз накладывающихся волн.
Уравне́ние Шрёдингера — линейное дифференциальное уравнение в частных производных, описывающее изменение в пространстве и во времени чистого состояния, задаваемого волновой функцией, в гамильтоновых квантовых системах.
Дифференциа́льная геоме́трия кривы́х — раздел дифференциальной геометрии, который занимается исследованием гладких пространственных и плоских кривых в евклидовом пространстве аналитическими методами.

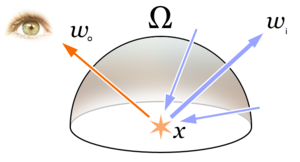
Ре́ндеринг или отрисо́вка — термин в компьютерной графике, обозначающий процесс получения изображения по модели с помощью компьютерной программы.
Волново́е число́ — быстрота роста фазы волны  по координате в пространстве:
по координате в пространстве:
 .
.
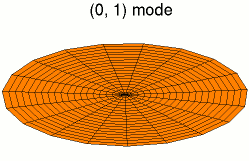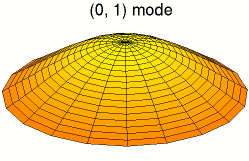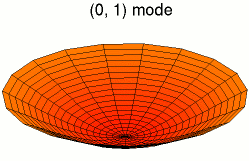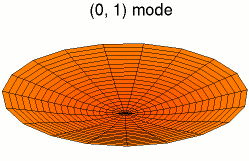
Стоя́чая волна́ — явление интерференции волн, распространяющихся в противоположных направлениях, при котором перенос энергии ослаблен или отсутствует.
Волна́ де Бро́йля — волна вероятности, определяющая плотность вероятности обнаружения объекта в заданном интервале конфигурационного пространства. В соответствии с принятой терминологией говорят, что волны де Бройля связаны с любыми частицами и отражают их волновую природу.
Эффе́кт Ке́рра, или квадрати́чный электроопти́ческий эффект, — явление изменения значения показателя преломления оптического материала пропорционально квадрату напряжённости приложенного электрического поля. Отличается от эффекта Поккельса тем, что изменение показателя прямо пропорционально квадрату электрического поля, в то время как последний изменяется линейно.
Волновое уравнение в физике — линейное гиперболическое дифференциальное уравнение в частных производных, задающее малые поперечные колебания тонкой мембраны или струны, а также другие колебательные процессы в сплошных средах и электромагнетизме (электродинамике). Находит применение и в других областях теоретической физики, например при описании гравитационных волн. Является одним из основных уравнений математической физики.

Фо́рмула Пла́нка — формула, описывающая спектральную плотность излучения, которое создаётся абсолютно чёрным телом определённой температуры. Формула была открыта Максом Планком в 1900 году и названа по его фамилии. Её открытие сопровождалось появлением гипотезы о том, что энергия может принимать только дискретные значения. Эта гипотеза некоторое время после открытия не считалась значимой, но, как принято считать, дала рождение квантовой физике.
Зако́н излуче́ния Кирхго́фа — физический закон, установленный немецким физиком Густавом Кирхгофом в 1859 году.
Фазированной антенной решёткой называют антенную решётку, фазой токов (поля) в каждом из элементов которой можно управлять.

Интерферометр Майкельсона — двухлучевой интерферометр, изобретённый Альбертом Майкельсоном. Данный прибор позволил впервые измерить длину волны света. В опыте Майкельсона интерферометр был использован Майкельсоном и Морли для проверки гипотезы о светоносном эфире в 1887 году.

Пло́ская волна́ — волна, фронт которой плоский.
Уравнение электромагнитной волны — дифференциальное уравнение в частных производных второго порядка, которое описывает распространение электромагнитных волн через среду или в вакуумe. Это трёхмерная форма волнового уравнения. Однородная форма уравнения, записанная в терминах либо электрического поля E, либо магнитного поля B, имеет вид: