Теория возмущений — метод приближённого решения задач теоретической физики, применимый в том случае, когда в задаче присутствует малый параметр, причём в пренебрежении этим параметром задача имеет точное решение.

Дифференциа́льное уравне́ние — уравнение, которое помимо функции содержит её производные. Порядок входящих в уравнение производных может быть различен. Производные, функции, независимые переменные и параметры могут входить в уравнение в различных комбинациях или отсутствовать вовсе, кроме хотя бы одной производной. Не любое уравнение, содержащее производные неизвестной функции, является дифференциальным. Например,  не является дифференциальным уравнением.
не является дифференциальным уравнением.

Уравнение теплопроводности — дифференциальное уравнение в частных производных второго порядка, которое описывает распределение температуры в заданной области пространства и ее изменение во времени.

Уравне́ния Ма́ксвелла — система уравнений в дифференциальной или интегральной форме, описывающих электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и сплошных средах. Вместе с выражением для силы Лоренца, задающим меру воздействия электромагнитного поля на заряженные частицы, эти уравнения образуют полную систему уравнений классической электродинамики, называемую иногда уравнениями Максвелла — Лоренца. Уравнения, сформулированные Джеймсом Клерком Максвеллом на основе накопленных к середине XIX века экспериментальных результатов, сыграли ключевую роль в развитии представлений теоретической физики и оказали сильное, зачастую решающее влияние не только на все области физики, непосредственно связанные с электромагнетизмом, но и на многие возникшие впоследствии фундаментальные теории, предмет которых не сводился к электромагнетизму.

Зако́ны Ке́плера — три эмпирических соотношения, установленные Иоганном Кеплером на основе длительных астрономических наблюдений Тихо Браге. Изложены Кеплером в работах, опубликованных между 1609 и 1619 годами. Описывают идеализированную гелиоцентрическую орбиту планеты.
Зада́ча Коши́ — одна из основных задач теории дифференциальных уравнений ; состоит в нахождении решения (интеграла) дифференциального уравнения, удовлетворяющего так называемым начальным условиям.
Уравне́ния Э́йлера — Лагра́нжа являются основными формулами вариационного исчисления, c помощью которых ищутся стационарные точки и экстремумы функционалов. В частности, эти уравнения широко используются в задачах оптимизации и совместно с принципом стационарности действия используются для вычисления траекторий в механике. В теоретической физике вообще это (классические) уравнения движения в контексте получения их из написанного явно выражения для действия (лагранжиана).
В математике и теоретической физике функциональная производная является обобщением производной по направлению. Разница заключается в том, что для последней дифференцирование производится в направлении какого-нибудь вектора, а для первой речь идёт о функции. Оба эти понятия можно рассматривать как обобщение обычного дифференциального исчисления.
В теории дифференциальных уравнений, начальные и граничные условия — дополнение к основному дифференциальному уравнению, задающее его поведение в начальный момент времени или на границе рассматриваемой области соответственно.
Обыкновенное дифференциальное уравне́ние (ОДУ) — дифференциальное уравнение для функции от одной переменной Таким образом, ОДУ — уравнения вида

Дифференциа́льное уравне́ние в ча́стных произво́дных — дифференциальное уравнение, содержащее неизвестные функции нескольких переменных и их частные производные.

Формула Ньютона — Лейбница, или основная формула анализа, или формула Барроу даёт соотношение между двумя операциями: взятием интеграла Римана и вычислением первообразной.

Быстро-медленная система в математике — это динамическая система, в которой присутствуют процессы, происходящие в разных масштабах времени. Фазовые переменные такой системы делятся на два класса: «быстрые» и «медленные» переменные. Скорость изменения «быстрых» переменных почти во всех точках фазового пространства много больше скорости изменения «медленных» переменных. Траектории таких систем состоят из чередующихся участков медленного «дрейфа» и быстрых «срывов». Быстро-медленные системы описывают различные физические и иные явления, в которых постепенное эволюционное накопление малых изменений со временем приводит к скачкообразному переходу системы на новый динамический режим.
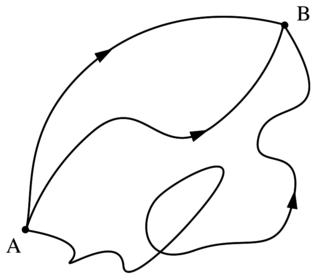
Формулировка квантовой механики через интеграл по траекториям — описание квантовой теории, которое обобщает принцип действия классической механики. Оно замещает классическое определение одиночной, уникальной траектории системы полной суммой по бесконечному множеству всевозможных траекторий для расчёта квантовой амплитуды. Методологически формулировка через интеграл по траекториям близка к принципу Гюйгенса — Френеля из классической теории волн.
Нормальная форма дифференциальных уравнений есть наипростейшая эквивалентная форма исходных уравнений. Нормальная форма получается с помощью специальных замен зависимых и независимых переменных задачи с целью максимального упрощения структуры уравнений. В математике эти замены переменных связаны с инфинитезимальными преобразованиями групп Ли. В физике вопросы, связанные с нормальной формой, получили отражение в теореме Эмми Нётер.
Метод Годунова — реализация схем сквозного счета, с помощью которых можно рассчитывать газодинамические течения с разрывами параметров внутри расчётной области. Эта схема предложена С. К. Годуновым в 1959 г. Метод Годунова — это вариант метода контрольного объёма. Потоки через боковые грани определяются из решения задачи о распаде произвольного разрыва. Поясним на примере.
Оптимальное управление — задача проектирования системы, обеспечивающей для заданного объекта управления или процесса закон управления или управляющую последовательность воздействий, обеспечивающих максимум или минимум заданной совокупности критериев качества системы.
Метод характеристик — метод решения дифференциальных уравнений в частных производных. Обычно применяется к решению уравнений в частных производных первого порядка, но он может быть применён и к решению гиперболических уравнений более высокого порядка.
В теории устойчивости решений дифференциальных уравнений функция Ляпунова — скалярная функция, используемая для исследования устойчивости решений обыкновенного дифференциального уравнения или системы обыкновенных дифференциальных уравнений с помощью второго (прямого) метода Ляпунова.
Метод функции Грина — метод решения линейного дифференциального уравнения, позволяет посредством нахождения соответствующей оператору этого уравнения функции Грина практически напрямую получить частное решение. Эффективность определяется возможностью записать функцию Грина в явном виде.
![{\displaystyle {\begin{cases}{\dfrac {dy}{dt}}=f(y,t,\varepsilon ),&t\in (0,T]\\y(0,\varepsilon )=y^{0}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9352245f38410ba326f25d9e0139ab2a78cca892)

![{\displaystyle {\begin{cases}\varepsilon {\dfrac {dy}{dt}}=f(y,t,\varepsilon ),&t\in (0,T]\\y(0,\varepsilon )=y^{0}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4918f56462e468f4c3ed5fd2bb2f6c740a1aafa8)











