Уравнения Петерсона ― Кодацци

Уравнения Петерсона ― Кодацци (или Петерсона ― Майнарди ― Кодацци) ― уравнения, составляющие вместе с уравнением Гаусса необходимые и достаточные условия интегрируемости системы, к которой сводится задача восстановления поверхности по её первой и второй квадратичным формам.

Уравнения

Уравнения Петерсона ― Майнарди ― Кодацци имеют вид

{\frac {\partial b_{i1}}{\partial u^{2}}}+\Gamma _{i1}^{1}b_{12}+\Gamma _{i1}^{2}b_{22}={\frac {\partial b_{i2}}{\partial u^{1}}}+\Gamma _{i2}^{1}b_{11}+\Gamma _{i2}^{2}b_{21}

где $b_{ij}$ ― коэффициенты второй квадратичной формы, $\Gamma _{jk}^{i}$ ― символы Кристоффеля.

Свойства

Теорема Бонне. Пусть $g=g_{ij}$ $g=g_{ij}$ и $b=b_{ij}$ $b=b_{ij}$ , $i,j\in \{1,2\}$ $i,j\in \{1,2\}$ две гладкие квадратичные формы заданые в односвязной области $U$ $U$ . Если $g$ $g$ и $b$ $b$ удовлетворяют уравнениям Петерсона ― Кодацци, тогда существует и притом единственная (с точностью до движений) поверхность в $\mathbb {R} ^{3}$ $\mathbb {R} ^{3}$ , для которой эти формы являются первой и второй квадратичными формами.
- Эту теорему также доказал Петерсон в своей диссертации.

История

Уравнения впервые найдены Петерсоном^[1] в 1853, переоткрыты Майнарди^[2] и Кодацци(1867)^[3].

Вариации и обобщения

Известен вариант уравнений для гиперповерхносей в пространствах старших размерностей, а также для произвольных коразмерностей.^[4]

Примечания

↑ Peterson, K. M. "Über die Biegung der Flächen." Dorpat. Kandidatenschrift. 1853.
↑ Mainardi, G. "Sulle coordinate curvilinee d'una superfice dello spazio." Giornale del R. Istituto Lombardo 9, 385—398, 1856.
↑ Codazzi, D. "Sulle coordinate curvilinee d'una superficie dello spazio." Ann. math. pura applicata 2, 101—19, 1868—1869.
↑ M. Dajczer and R. Tojeiro. Submanifold theory. Universitext. Beyond an introduction. Springer, New York, 2019

Литература

Рашевский П. К., Курс дифференциальной геометрии, М., 1956.
Топоногов, В. А. Дифференциальная геометрия кривых и поверхностей. — Физматкнига, 2012. — ISBN 978-5-89155-213-5.

Похожие исследовательские статьи

Уравнение Дира́ка — релятивистски инвариантное уравнение движения для биспинорного классического поля электрона, применимое также для описания других точечных фермионов со спином 1/2; установлено Полем Дираком в 1928 году.

Си́ла Ло́ренца — сила, с которой электромагнитное поле, согласно классической (неквантовой) электродинамике, действует на точечную заряженную частицу. Иногда силой Лоренца называют силу, действующую на движущийся со скоростью $\text{[math]}$ заряд $\text{[math]}$ лишь со стороны магнитного поля, нередко же полную силу — со стороны электромагнитного поля вообще, иначе говоря, со стороны электрического $\text{[math]}$ и магнитного $\text{[math]}$ полей. В Международной системе единиц (СИ) выражается как:

Основная теорема римановой геометрии утверждает, что на любом римановом многообразии имеется единственная метрическая связность без кручения, называемая связностью Леви-Чивиты данной метрики. Здесь метрическая связность — это связность, сохраняющая метрический тензор.

<span class="mw-page-title-main">Параболическое уравнение</span>

Параболические уравнения — класс дифференциальных уравнений в частных производных. Один из видов уравнений, описывающих нестационарные процессы.

Эллиптический оператор — дифференциальный оператор 2-го порядка в частных производных. Является частным случаем гипоэлиптического оператора

Эллиптические уравнения — класс дифференциальных уравнений в частных производных, описывающих стационарные процессы.

Дифференциа́льное уравне́ние в ча́стных произво́дных — дифференциальное уравнение, содержащее неизвестные функции нескольких переменных и их частные производные.

Си́мволы Кристо́ффеля — коэффициенты координатного выражения аффинной связности, в частности, связности Леви-Чивиты. Названы в честь Эльвина Бруно Кристоффеля. Используются в дифференциальной геометрии, общей теории относительности и близких к ней теориях гравитации. Появляются в координатном выражении тензора кривизны. При этом сами символы тензорами не являются.

Теория Калуцы — Клейна — одна из многомерных теорий гравитации, позволяющая объединить два фундаментальных физических взаимодействия: гравитацию и электромагнетизм. Теория была впервые опубликована в 1921 году немецким математиком Теодором Калуцей, который расширил пространство Минковского до 5-мерного пространства и получил из уравнений своей теории уравнения общей теории относительности и классические уравнения Максвелла. Обоснование ненаблюдаемости пятого измерения было предложено шведским физиком Оскаром Клейном в 1926 году.

Вселе́нная Фри́дмана — одна из космологических моделей, удовлетворяющих полевым уравнениям общей теории относительности (ОТО), первая из нестационарных моделей Вселенной. Получена Александром Фридманом в 1922. Модель Фридмана описывает однородную изотропную в общем случае нестационарную Вселенную с веществом, обладающую положительной, нулевой или отрицательной постоянной кривизной. Эта работа учёного стала первым основным теоретическим развитием ОТО после работ Эйнштейна 1915—1917 гг.

Вторая квадратичная форма поверхности ― квадратичная форма на касательном расслоении поверхности, которая, в отличие от первой квадратичной формы, определяет внешнюю геометрию поверхности в окрестности данной точки.

Фи́нслерова геометрия — одно из обобщений римановой геометрии. В финслеровой геометрии рассматриваются многообразия с финслеровой метрикой; то есть выбором нормы на каждом касательном пространстве, которая гладко меняется от точки к точке.

<span class="mw-page-title-main">Теорема о равнораспределении</span>

Теорема о равнораспределении кинетической энергии по степеням свободы, закон равнораспределения, теорема о равнораспределении — связывает температуру системы с её средней энергией в классической статистической механике. В первоначальном виде теорема утверждала, что при тепловом равновесии энергия разделена одинаково между её различными формами, например, средняя кинетическая энергия поступательного движения молекулы должна равняться средней кинетической энергии её вращательного движения.

<span class="mw-page-title-main">Нормальные колебания</span>

Норма́льные колеба́ния, со́бственные колебания или мо́ды — набор характерных для колебательной системы типов гармонических колебаний. Каждое из нормальных колебаний физической системы, например, колебаний атомов в молекулах, характеризуется своей частотой. Такая частота называется нормальной частотой, или собственной частотой. Набор частот нормальных колебаний составляет колебательный спектр. Произвольное колебание физической системы можно представить в виде суперпозиции различных нормальных колебаний. Вынужденные колебания физической системы испытывают резонанс на частотах, которые совпадают с частотами нормальных колебаний этой системы.

Геодезическая кривизна $\text{[math]}$ кривой $\text{[math]}$ в римановой геометрии измеряет, насколько далеко кривая отличается от геодезической. Например, для 1D кривой на 2D поверхности, вложенной в 3D пространство, это кривизна кривой, спроецированной на плоскость, касательную к поверхности. Более обще, в заданном многообразии $\text{[math]}$ геодезическая кривизна ― это обычная кривизна кривой $\text{[math]}$ . Однако если кривая $\text{[math]}$ лежит в подмногообразии $\text{[math]}$ многообразия $\text{[math]}$ , геодезическая кривизна относится к кривизне $\text{[math]}$ в $\text{[math]}$ , и она отличается в общем виде от кривизны $\text{[math]}$ в объемлющем многообразии $\text{[math]}$ . (Объемлющая) кривизна $\text{[math]}$ кривой $\text{[math]}$ зависит от двух факторов ― кривизны подмногообразия $\text{[math]}$ в направлении $\text{[math]}$ , которая зависит только от направления кривой и кривизны $\text{[math]}$ в многообразии $\text{[math]}$ , которая является величиной второго порядка. Связь между ними ― $\text{[math]}$ . В частности, геодезические на $\text{[math]}$ имеют нулевую геодезическую кривизну («прямые»), так что $\text{[math]}$ .

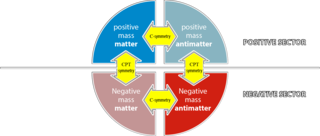
Биметрические теория гравитации — альтернативные теории гравитации, в которых вместо одного метрического тензора используются два или более. Часто вторая метрика вводится только при высоких энергиях, в предположении, что скорость света может зависеть от энергии. Наиболее известными примерами биметрических теорий являются теория Розена и релятивистская теория гравитации.

Уравне́ние Ланда́у — Ли́фшица — уравнение, описывающее движение намагниченности в приближении континуальной модели в твердых телах. Впервые введено Л. Д. Ландау и Е. М. Лифшицем в 1935 году.

Параметризо́ванный постнью́тоновский формали́зм — версия постньютоновского формализма, применимая не только к общей теории относительности, но и к другим метрическим теориям гравитации, когда движения тел удовлетворяют принципу эквивалентности Эйнштейна. В таком подходе явно выписываются все возможные зависимости гравитационного поля от распределения материи вплоть до соответствующего порядка обратного квадрата скорости света $\text{[math]}$ и составляется наиболее общее выражение для решения уравнений гравитационного поля и движения материи. Различные теории гравитации при этом предсказывают различные значения коэффициентов — так называемых ППН параметров — в общих выражениях. Это приводит к потенциально наблюдаемым эффектам, экспериментальные ограничения на величину которых приводят к ограничениям на ППН параметры, и соответственно — к ограничениям на теории гравитации, их предсказывающие. Можно сказать, что ППН параметры описывают различия между ньютоновой и описываемой теорией гравитации. ППН формализм применим когда гравитационные поля слабы, а скорости движения формирующих их тел малы по сравнению со скоростью света — каноническими примерами применения являются движение Солнечной системы и систем пульсаров в двойных системах.

Формула Фейнмана — Каца — математическая формула, устанавливающая связь между дифференциальными уравнениями с частными производными и случайными процессами. Названа в честь физика Ричарда Фейнмана и математика Марка Каца.

Разрывный метод Галёркина — метод решения операторных уравнений, в основном дифференциальных уравнений. Является развитием классического метода конечных элементов (МКЭ), основанного на вариационной постановке Галёркина.

Эта страница основана на статье Википедии.
Текст доступен на условиях лицензии CC BY-SA 4.0; могут применяться дополнительные условия.
Изображения, видео и звуки доступны по их собственным лицензиям.