Условие Слуцкого — условие эргодичности случайного процесса:
Необходимым и достаточным условием эргодичности относительно среднего стационарного случайного процесса с корреляционной функцией 
Названо в честь советского учёного Е. Е. Слуцкого.
Случайная величина — переменная, значения которой представляют собой численные исходы некоторого случайного феномена или эксперимента. Другими словами, это численное выражение результата случайного события. Случайная величина является одним из основных понятий теории вероятностей. Для обозначения случайной величины в математике принято использовать греческую букву «кси» 
Математи́ческое ожида́ние — понятие в теории вероятностей, означающее среднее значение случайной величины. В случае непрерывной случайной величины подразумевается взвешивание по плотности распределения. Математическое ожидание случайного вектора равно вектору, компоненты которого равны математическим ожиданиям компонентов случайного вектора.
Уравнение диффузии представляет собой частный вид дифференциального уравнения в частных производных. Бывает нестационарным и стационарным.
Корреля́ция, или корреляцио́нная зави́симость — статистическая взаимосвязь двух или более случайных величин, при этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин.
Полимериза́ция — процесс образования высокомолекулярного вещества (полимера) путём многократного присоединения молекул низкомолекулярного вещества к активным центрам в растущей молекуле полимера. Молекула мономера, входящая в состав полимера, образует так называемое мономерное (структурное) звено. Элементный состав мономера и полимера приблизительно одинаков.
Случа́йный проце́сс в теории вероятностей — семейство случайных величин, индексированных некоторым параметром, чаще всего играющим роль времени или координаты.
Распределение вероятностей — это закон, описывающий область значений случайной величины и вероятности их исхода (появления).
Самоорганизу́ющаяся ка́рта Ко́хонена — нейронная сеть с обучением без учителя, выполняющая задачу визуализации и кластеризации. Идея сети предложена финским учёным Т. Кохоненом. Является методом проецирования многомерного пространства в пространство с более низкой размерностью, применяется также для решения задач моделирования, прогнозирования, выявление наборов независимых признаков, поиска закономерностей в больших массивах данных, разработке компьютерных игр, квантизации цветов к их ограниченному числу индексов в цветовой палитре: при печати на принтере и ранее на ПК или же на приставках с дисплеем с пониженным числом цветов, для архиваторов [общего назначения] или видео-кодеков, и прч. Является одной из версий нейронных сетей Кохонена.
Методы Мо́нте-Ка́рло (ММК) — группа численных методов для изучения случайных процессов. Суть метода заключается в следующем: процесс описывается математической моделью с использованием генератора случайных величин, модель многократно обсчитывается, на основе полученных данных вычисляются вероятностные характеристики рассматриваемого процесса. Например, чтобы узнать методом Монте-Карло, какое в среднем будет расстояние между двумя случайными точками в круге, нужно взять координаты большого числа случайных пар точек в границах заданной окружности, для каждой пары вычислить расстояние, а потом для них посчитать среднее арифметическое.
Ма́рковский проце́сс — случайный процесс, эволюция которого после любого заданного значения временно́го параметра 
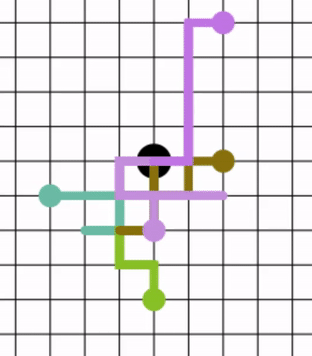
Случайное блуждание — математический объект, известный как стохастический или случайный процесс, который описывает путь, состоящий из последовательности случайных шагов в каком-нибудь математическом пространстве.
Центра́льные преде́льные теоре́мы (ЦПТ) — класс теорем в теории вероятностей, утверждающих, что сумма достаточно большого количества слабо зависимых случайных величин, имеющих примерно одинаковые масштабы, имеет распределение, близкое к нормальному.
Сходи́мость по распределе́нию в теории вероятностей — вид сходимости случайных величин.
Мартинга́л в теории случайных процессов — такой случайный процесс, что наилучшим предсказанием поведения процесса в будущем является его настоящее состояние.
Эргодичность — специальное свойство некоторых динамических систем, состоящее в том, что в процессе эволюции почти каждое состояние с определённой вероятностью проходит вблизи любого другого состояния системы.
Стохастическое дифференциальное уравнение (СДУ) — дифференциальное уравнение, в котором один член или более имеют стохастическую природу, то есть представляют собой стохастический (случайный) процесс. Таким образом, решения уравнения также оказываются стохастическими процессами. Наиболее известный и часто используемый пример СДУ — уравнение с членом, описывающим белый шум. Однако существуют и другие типы случайных флуктуаций, например скачкообразный процесс.
Эргодическая теорема Биркгофа — Хинчина утверждает, что для динамической системы, сохраняющей меру, и интегрируемой по этой мере функции на пространстве для почти всех начальных точек соответствующие им временны́е средние сходятся. Более того, если инвариантная мера эргодична, то для почти всех начальных точек предел один и тот же — интеграл функции по данной мере. Этот принцип формулируется как «временно́е среднее для почти всех начальных точек равно пространственному».
Коррелятор — специализированное устройство для автоматического вычисления корреляционных функций и взаимных корреляционных функций стационарных случайных процессов.
Экзогенность — буквально «внешнее происхождение» — свойство факторов эконометрических моделей, заключающееся в предопределённости, заданности их значений, независимости от функционирования моделируемой системы. Экзогенность противоположна эндогенности. Значения экзогенных переменных определяются вне модели, и на их основе в рамках рассматриваемой модели определяются значения эндогенных переменных.
Формула Фейнмана — Каца — математическая формула, устанавливающая связь между дифференциальными уравнениями с частными производными и случайными процессами. Названа в честь физика Ричарда Фейнмана и математика Марка Каца.
