Устранимость сечений

Устранимость сечений (теорема Генцена, элиминационная теорема) — свойство логических исчислений, согласно которому всякую секвенцию, выводимую в данном исчислении, можно вывести без применения правила сечений^[1]. Играет фундаментальную роль в теории доказательств и важную методологическую роль в математической логике в целом в связи с тем, что предоставляет конструктивный метод доказательства непротиворечивости, в частности, для классической и интуиционистской логик первого порядка^[2].

Для классического и интуиционистского исчислений секвенций свойство доказано Генценом в 1934 году. В 1953 году высказана гипотеза Такеути, согласно которой устранимость сечений имеет место для простой теории типов и соответствующих ей логик высших порядков, впоследствии она нашла подтверждение — для классической логики второго порядка устранимость сечений доказал Тейт^[англ.], для простой теории типов — Такахаси и Правица^[швед.], вскоре найдены доказательства для серии неклассических теорий высших порядков (Драгалин) и развитых теорий типов (Жирар^[англ.] для системы F).

Символическая формулировка: пусть $\Gamma \vdash \Theta ,\Phi$ и $\Phi ,\Lambda \vdash \Delta$ — доказуемые секвенции исчисления $G$ ; если $\Gamma ,\Lambda \vdash \Delta ,\Theta$ — секвенция исчисления $G$ , то она доказуема^[3].

Примечания

↑ Теория доказательств, 1978, с. 29.
↑ П. И. Быстров. Элиминационная теорема // Новая философская энциклопедия : в 4 т. / пред. науч.-ред. совета В. С. Стёпин. — 2-е изд., испр. и доп. — М. : Мысль, 2010. — 2816 с.
↑ Ершов, 1987, с. 214.

Литература

G. Gentzen. Untersuchungen über das logische Schließen (нем.) // Mathematische Zeitschrift. — 1934–1935. — Bd. 39. — S. 405–431. — doi:10.1007/BF01201363.
Такеути Г. Теория доказательств. — М.: Мир, 1978. — 412 с.
Ершов Ю. Л., Палютин Е. А. Математическая логика. — М.: Наука, 1987. — 336 с.

Похожие исследовательские статьи

Га́мма-распределе́ние в теории вероятностей — это двухпараметрическое семейство абсолютно непрерывных распределений. Если параметр $\text{[math]}$ принимает целое значение, то такое гамма-распределение также называется распределе́нием Эрла́нга.

Си́мволы Кристо́ффеля — коэффициенты координатного выражения аффинной связности, в частности, связности Леви-Чивиты. Названы в честь Эльвина Бруно Кристоффеля. Используются в дифференциальной геометрии, общей теории относительности и близких к ней теориях гравитации. Появляются в координатном выражении тензора кривизны. При этом сами символы тензорами не являются.

Сферическая система координат — трёхмерная система координат, в которой каждая точка пространства определяется тремя числами $\text{[math]}$ , где $\text{[math]}$ — расстояние до начала координат, а $\text{[math]}$ и $\text{[math]}$ — зенитный и азимутальный углы соответственно.

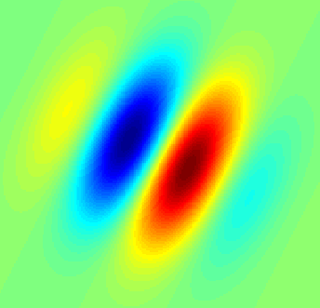
Фильтр Габора — линейный электронный фильтр, импульсная переходная характеристика которого определяется в виде гармонической функции, помноженной на гауссиан. При цифровой обработке изображений этот фильтр применяется для распознавания границ объектов.

Теория доказательств — раздел математической логики, представляющий доказательства в виде формальных математических объектов, осуществляя их анализ с помощью математических методов. Доказательства обычно представляются в виде индуктивно определённых структур данных, таких как списки и деревья, созданных в соответствии с аксиомами и правилами вывода формальных систем. Таким образом, теория доказательств является синтаксической, в отличие от семантической теории моделей. Вместе с теорией моделей, аксиоматической теорией множеств и теорией вычислений, теория доказательств является одним из так называемых «четырёх столпов» математики. Теория доказательств использует точное определение понятия доказательства при доказательстве невозможности доказательства того или иного предложения в рамках заданной математической теории.

Теоре́ма Гёделя о полноте́ исчисле́ния предика́тов является одной из фундаментальных теорем математической логики: она устанавливает однозначную связь между логической истинностью высказывания и его выводимостью в логике первого порядка. Впервые эта теорема была доказана Куртом Гёделем в 1929.

В байесовской статистике априорная вероятность Джеффри, по имени Гарольда Джеффри — неинформативная (объективная) априорная вероятность в пространстве параметра, пропорциональная квадратному корню из детерминанта информации Фишера:

\text{[math]}

Уравне́ние Ланда́у — Ли́фшица — уравнение, описывающее движение намагниченности в приближении континуальной модели в твердых телах. Впервые введено Л. Д. Ландау и Е. М. Лифшицем в 1935 году.

Теория Эйнштейна — Картана (ЭК) была разработана как расширение общей теории относительности, внутренне включающее в себя описание воздействия на пространство-время кроме энергии-импульса также и спина материальных полей. В теории ЭК вводится аффинное кручение, а вместо псевдоримановой геометрии для пространства-времени используется геометрия Римана — Картана. В результате от метрической теории переходят к аффинной теории пространства-времени. Результирующие уравнения для описания пространства-времени распадаются на два класса. Один из них аналогичен общей теории относительности, с тем отличием, что в тензор кривизны включены компоненты с аффинным кручением. Второй класс уравнений задаёт связь тензора кручения и тензора спина материи и излучения. Получаемые поправки к общей теории относительности в условиях современной Вселенной настолько малы, что пока не видно даже гипотетических путей для их измерения.

Пропагатор в квантовой механике и квантовой теории поля (КТП) — функция, характеризующая распространение релятивистского поля от одного акта взаимодействия до другого. Эта функция определяет амплитуду вероятности перемещения частицы из одного места пространства в другое за заданный промежуток времени или перемещения частицы с определённой энергией и импульсом. Для расчёта частоты столкновений в КТП используются виртуальные частицы, представленные в диаграммах Фейнмана пропагаторами, вносят свой вклад в вероятность рассеяния, описываемого соответствующей диаграммой. Их также можно рассматривать как оператор, обратный волновому оператору, соответствующему частице, и поэтому их часто называют (причинными) функциями Грина.

Достаточная статистика для параметра $\text{[math]}$ определяющая некоторое семейство $\text{[math]}$ распределений вероятности — статистика $\text{[math]}$ такая, что условная вероятность выборки $\text{[math]}$ при данном значении $\text{[math]}$ не зависит от параметра $\text{[math]}$ То есть выполняется равенство:

\text{[math]}

Статическая изотропная метрика — это метрика, определяющая статическое изотропное гравитационное поле. Частным случаем этой метрики является метрика Шварцшильда, на случай пустого пространства-времени.

Просто типизированное лямбда-исчисление — система типизированного лямбда-исчисления, в которой лямбда-абстракции приписывается специальный «стрелочный» тип. Эта система была предложена Алонзо Чёрчем в 1940 году. Для близкого к лямбда-исчислению формализма комбинаторной логики похожая система рассматривалась Хаскеллом Карри в 1934 году.

В математике лагранжевой системой называется пара $\text{[math]}$ гладкого расслоения $\text{[math]}$ и лагранжевой плотности $\text{[math]}$ , которая определяет дифференциальный оператор Эйлера — Лагранжа, действующий на сечения расслоения $\text{[math]}$ .

Сечение в теории доказательств — правило вывода, позволяющее удалить («высечь») промежуточное высказывание $\text{[math]}$ :

\text{[math]}

Гипотеза Такеути — утверждение об устранимости сечений в исчислении секвенций для простой теории типов, построенной Гаиси Такеути в 1953 году. Методологическая важность гипотезы состояла в том, что устранимость сечений для этого исчисления открывает путь к доказательствам корректности, непротиворечивости и полноты для широкого класса логик высших порядков, по аналогии с результатом Генцена 1934 года для классического и интуиционистского исчислений предикатов первого порядка.

Теорема о дедукции — один из фундаментальных результатов в теории доказательств, формализует способ рассуждения, при котором для установления импликации $\text{[math]}$ используется $\text{[math]}$ в качестве необходимого условия вывода. Используется для установления существования выводов и доказательств, не используя их построения. Впервые была явно сформулирована и доказана в 1930 году Эрбраном, а без доказательств использовалась Эрбраном в 1928 году. Независимо этот принцип был сформулирован Тарским в 1930 году. По сообщению Тарского, он знал и применял этот принцип еще в 1921 году.

Исчисление секвенций — вариант логических исчислений, использующий для доказательства утверждений не произвольные цепочки тавтологий, а последовательности условных суждений — секвенций. Наиболее известные исчисления секвенций — $\text{[math]}$ и $\text{[math]}$ для классического и интуиционистского исчислений предикатов — построены Генценом в 1934 году, позднее сформулированы секвенциальные варианты для широкого класса прикладных исчислений, теорий типов, неклассических логик.

Исчисление Ламбека — формальная логическая система, предложенная в 1958 году Иоахимом Ламбеком, которая предназначена для описания синтаксиса естественных языков. С математической точки зрения исчисление Ламбека является фрагментом линейной логики.

Субструктурная логика — логика, в которой отсутствует одно из обычных cтруктурных правил, таких как ослабление, контракция, обмен или ассоциативность. Двумя наиболее значимыми субструктурными логиками являются релевантная и линейная.

Эта страница основана на статье Википедии.
Текст доступен на условиях лицензии CC BY-SA 4.0; могут применяться дополнительные условия.
Изображения, видео и звуки доступны по их собственным лицензиям.