
Случа́йный проце́сс в теории вероятностей — семейство случайных величин, индексированных некоторым параметром, чаще всего играющим роль времени или координаты.

Экспоненциа́льное распределе́ние — абсолютно непрерывное распределение, моделирующее время между двумя последовательными свершениями одного и того же события.

Центра́льные преде́льные теоре́мы (ЦПТ) — класс теорем в теории вероятностей, утверждающих, что сумма достаточно большого количества слабо зависимых случайных величин, имеющих примерно одинаковые масштабы, имеет распределение, близкое к нормальному.
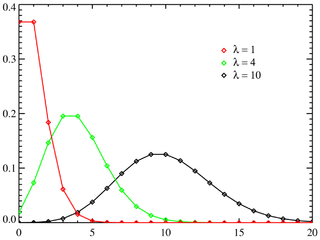
Распределе́ние Пуассо́на — распределение дискретного типа случайной величины, представляющей собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.
Пло́тность вероя́тности — один из способов задания распределения случайной величины. Во многих практических приложениях понятия «плотность вероятности» и «плотность (распределения) случайной величины» или «функция распределения вероятностей» фактически синонимизируются и под ними подразумевается вещественная функция, характеризующая сравнительную вероятность реализации тех или иных значений случайной переменной (переменных).

Га́мма-распределе́ние в теории вероятностей — это двухпараметрическое семейство абсолютно непрерывных распределений. Если параметр  принимает целое значение, то такое гамма-распределение также называется распределе́нием Эрла́нга.
принимает целое значение, то такое гамма-распределение также называется распределе́нием Эрла́нга.
Космологическое (метагалактическое) красное смещение — наблюдаемое для всех далёких источников понижение частот излучения, объясняемое как динамическое удаление этих источников друг от друга и, в частности, от нашей Галактики, то есть как нестационарность (расширение) Метагалактики.
Усто́йчивое распределе́ние в теории вероятностей — это такое распределение, которое может быть получено как предел по распределению сумм независимых случайных величин.
Процесс Пуассона, поток Пуассона, пуассоновский процесс — ординарный поток однородных событий, для которого число событий в интервале А не зависит от чисел событий в любых интервалах, не пересекающихся с А, и подчиняется распределению Пуассона. В теории случайных процессов описывает количество наступивших случайных событий, происходящих с постоянной интенсивностью.
Интегра́льное уравне́ние — функциональное уравнение, содержащее интегральное преобразование над неизвестной функцией. Если интегральное уравнение содержит также производные от неизвестной функции, то говорят об интегро-дифференциальном уравнении.
Метод опорных векторов — набор схожих алгоритмов обучения с учителем, использующихся для задач классификации и регрессионного анализа. Принадлежит семейству линейных классификаторов и может также рассматриваться как частный случай регуляризации по Тихонову. Особым свойством метода опорных векторов является непрерывное уменьшение эмпирической ошибки классификации и увеличение зазора, поэтому метод также известен как метод классификатора с максимальным зазором.
Модель Крамера — Лундберга — математическая модель, позволяющая оценивать риски разорения страховой компании. В рамках данной модели предполагается, что страховые взносы поступают равномерно, со скоростью с условных денежных единиц за единицу времени, где с — размер страховой премии. Модель позволяет определить размер страховой премии, необходимой для неразорения компании.
Важным принципиальным вопросом теории дискретизации является вопрос об объёме дискретного описания сигналов, то есть о количестве  базисных функций, используемых для представления:
базисных функций, используемых для представления:
 .
.
Теорема Риса — Фишера — утверждение функционального анализа об изометричности и изоморфности пространства Лебега  и пространства Гильберта
и пространства Гильберта  .
.
Стохастический интеграл — интеграл вида  , где
, где  — случайный процесс с независимыми нормальными приращениями. Стохастические интегралы широко используются в стохастических дифференциальных уравнениях. Стохастический интеграл нельзя вычислять как обычный интеграл Стилтьеса.
— случайный процесс с независимыми нормальными приращениями. Стохастические интегралы широко используются в стохастических дифференциальных уравнениях. Стохастический интеграл нельзя вычислять как обычный интеграл Стилтьеса.
Количество степеней свободы — это количество значений в итоговом вычислении статистики, способных варьироваться. Иными словами, количество степеней свободы показывает размерность вектора из случайных величин, количество «свободных» величин, необходимых для того, чтобы полностью определить вектор.
То́ждество Полла́чека — Спи́тцера — тождество, связывающее характеристическую функцию сумм независимых случайных величин.
В данной статье приведен список различных квадратурных формул, для численного интегрирования.
Теорема Бохнера — Хинчина — в теории вероятностей: теорема о необходимых и достаточных условиях для того, чтобы функция была характеристической; в теории случайных процессов: теорема о свойствах корреляционной функции стационарных процессов.


![{\displaystyle 1-z\phi (\lambda )=[1-M(e^{i\lambda \chi _{+}^{0}}z^{\eta _{+}^{0}});\eta _{+}^{0}<\infty ]D^{-1}(z)[1-M(e^{i\lambda \chi _{-}^{0}}z^{\eta _{-}^{0}});\eta _{-}^{0}<\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d452cf97e3db917177fd0484fe57c29279029f3b)


























