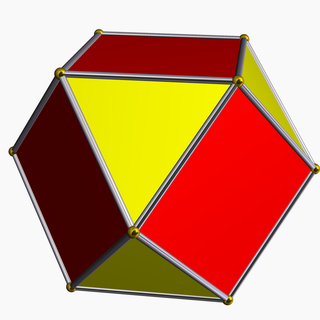
Фасета (геометрия)

Фасета в геометрии — элемент многогранника или связанной геометрической структуры, как правило на единицу меньшей размерности самой структуры.

В трёхмерном пространстве фасета многогранника — любой многоугольник, вершины которого являются вершинами многогранника, но который сам не является гранью^[1]^[2]. Огранка многогранника — нахождение и объединение фасет, которые образуют новый многогранник. Процесс является обратным образованию звёздчатой формы и может быть применён к многогранникам высоких размерностей^[3].
В комбинаторике многогранников и общей теории многогранников фасета многогранника размерности n — грань, имеющая размерность n−1. Фасеты можно назвать (n−1)-гранями или гипергранями^[4]^[5]. В трёхмерной геометрии они часто называются «гранями» без дальнейших уточнений^[6].
Фасета симплициального комплекса — максимальный симплекс, не являющейся гранью другого симплекса комплекса^[7]. Для симплициальных многогранников это совпадает с комбинаторным определением.

Примечания

↑ Bridge, 1974, с. 548—552.
↑ Inchbald, 2006, с. 253—261.
↑ Coxeter, 1973, с. 95.
↑ Максименко А. Н. Характеристики сложности: кликовое число графа многогранника и число прямоугольного покрытия : [арх. 12 октября 2016] // Модел. и анализ информ. систем.. — 2014. — Т. 21, № 5. — С. 117.
↑ Итоги науки и техники. — ВИНИТИ, 1979. — С. 69. — 160 с. Архивировано 29 июля 2016 года.
↑ Matoušek, 2002, с. 86.
↑ De Loera, Jesús A.; Rambau, Jörg; Santos, Francisco (2010), Triangulations: Structures for Algorithms and Applications, Algorithms and Computation in Mathematics, vol. 25, Springer, p. 493, ISBN 9783642129711.

Литература

N. J. Bridge. Facetting the dodecahedron // Acta crystallographica. — 1974. — Вып. A30.
G. Inchbald. Facetting diagrams // The mathematical gazette. — 2006. — Вып. 90.
H. S. M. Coxeter. Regular Polytopes^[англ.]. — 3rd (1947, 63, 73). — New York: Dover Publications Inc., 1973. — ISBN 0-486-61480-8.
Jiří Matoušek. 5.3 Faces of a Convex Polytope // Lectures in Discrete Geometry. — Springer, 2002. — P. 86. — (Graduate Texts in Mathematics).
Jesús A. De Loera, Jörg Rambau, Francisco Santos. Triangulations: Structures for Algorithms and Applications. — Springer, 2010. — Т. 25. — (Algorithms and Computation in Mathematics). — ISBN 9783642129711.
Деза М. М., Лоран М. Геометрия разрезов и метрик. — М.: МЦНМО, 2001. — ISBN 3-540-61611-X.
Р. Ю. Симанчёв. О ранговых неравенствах, порождающих фасеты многогранника связных k-факторов // Дискретн. анализ и исслед. опер.. — 1996. — Т. 3, вып. 3. — С. 84—110.
Р. Ю. Симанчёв, И. В. Уразова. О гранях многогранника задачи аппроксимации графа // Дискретный анализ и исследование операций. — 2015. — Март-апрель (т. 22, вып. 2). — С. 86—101. — doi:10.17377/daio.2015.22.469.
Ф. Схрейвер. Глава 8.4 "Фасеты" // Теория линейного и целочисленного программирования. — М., 1991. — Т. 2. — С. 157. — ISBN 5-03-002753-6.
Селиверстов А. В. Замечания о расположениях точек на квадриках // Модел. и анализ информ. систем. — 2012. — Т. 19, вып. 4. — С. 72—77.
Г. Г. Болоташвили. Простые нецелочисленные вершины релаксационного многогранника для задачи линейных порядков и отсекающие фасеты // Дискретная математика, алгебра и их приложения. Международная научная конференция, тезисы докладов. — Минск, Республика Беларусь: Институт математики НАН Беларуси, 2015, 14—18 сентября. — С. 91—92. — ISBN 978-986-6499-86-2.
Геометрия разрезов и метрик. — М.: МЦНМО, 2001. — ISBN 5-900916-84-7. — ISBN 3-540-61611-X.
Йосвиг М. Группа проективностей и раскраска фасет простого многогранника // Успехи математических наук. — 2001. — Т. 56, вып. 3. — С. 171—172.
Николаев А. В. Раздел 2.2 Фасеты и целочисленные вершины. // Диссертация: Свойства вершин релаксаций разрезного многогранника. — 2011. — (Диссертация).