Фаска (геометрия)

Куб без фаски, с небольшой фаской и с глубокой фаской

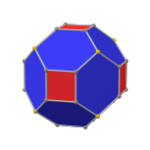
Фаска или усечение рёбер в геометрии — это топологическая операция, которая преобразует многогранник в другой многогранник. Операция подобна растяжению, передвигающему грани, удаляя их от центра. Для трёхмерных многогранников операция фаски добавляет новую шестиугольную грань вместо каждого исходного ребра.

В нотации Конвея операция представляется буквой c. Многогранник с e рёбрами будет иметь после операции фаски 2e новых вершин, 3e новых рёбер и e новых шестиугольных граней.

Правильный многогранник с фаской

В разделах ниже описаны детально пять правильных многогранников с фаской. Каждый показан в версии с рёбрами одинаковой длины и в канонической версии, в которой все рёбра касаются одной и той же полувписанной сферы. (Они выглядят заметно по-другому для тел, содержащих треугольные грани.) Показанные двойственные многогранники являются двойственными для канонических версий.

Исходный	{3,3}	{4,3}	{3,4}	{5,3}	{3,5}
С фаской

Тетраэдр с фаской

Тетраэдр с фаской
(с равными длинами рёбер)
Нотация Конвея	cT
Многогранник Голдберга^[англ.]	GP_III(2,0) = {3+,3}_2,0
Граней	4 треугольника 6 шестиугольников
Рёбер	24 (2 типа)
Вершин	16 (2 типа)
Конфигурация вершины	(12) 3.6.6 (4) 6.6.6
Группы симметрии	Тетраэдральная (T_d)
Двойственный многогранник	альтернированный триакисоктаэдр
Свойства	выпуклый, грани равносторонние
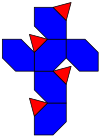развёртка

Тетраэдр с фаской (или альтернировнный усечённый куб) — это выпуклый многогранник, построенный как альтернированно^[англ.] усечённый куб или как операция фаски на тетраэдре, заменяющая его 6 рёбер шестиугольниками.

Многогранник является многогранником Голдберга^[англ.] G_III(2,0), содержащим треугольные и шестиугольные грани.

Фаски тетраэдра и связанные тела
тетраэдр с фаской (канонический)	двойственный для тетратетраэдра (октаэдра)	тетраэдр с фаской (канонический)
альтернированный триакисоктаэдр	октаэдр	альтернированный триакисоктаэдр

Куб с фаской

Куб с фаской
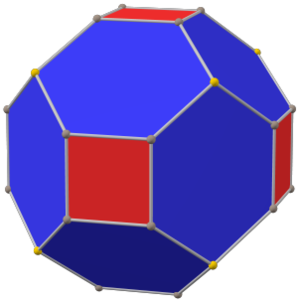(с равными длинами сторон)
Нотация Конвея	cC = t4daC
Многогранник Голдберга^[англ.]	GP_IV(2,0) = {4+,3}_2,0
Вершин	6 квадратов 12 шестиугольников
Рёбер	48 (2 типа)
Вершин	32 (2 типа)
Конфигурация вершины	(24) 4.6.6 (8) 6.6.6
Симметрия	O_h^[англ.], [4,3], (432) T_h, [4,3⁺], (32)
Двойственный многогранник	Тетракискубооктаэдр^[англ.]
Свойства	выпуклый, зоноэдр, грани равносторонние
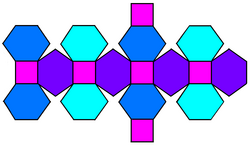развёртка

Куб с фаской — выпуклый многогранник с 32 вершинами, 48 рёбрами и 18 гранями — 12 шестиугольников и 8 квадратов. Многогранник строится как снятие фаски у куба. Квадраты уменьшаются в размерах и новые шестиугольные грани добавляются вместо всех исходных рёбер. Его двойственным является тетракискубооктаэдр^[англ.].

Многогранник не совсем точно называется усечённым ромбододекаэдром, хотя это имя и предполагает ромбокубооктаэдр. Более правильно называть его четыреусечённым ромбододекаэдром, поскольку усекаются только вершины порядка 4.

Шестиугольные грани являются равносторонними, но не являются правильными. Они образуются усечёнными ромбами, имеют 2 внутренних угла около 109.47° (= $\cos ^{-1}(-{\frac {1}{3}})$ ) и 4 внутренних угла 125.26°, в то время как у правильного шестиугольника все углы равны 120°.

Поскольку все грани многогранника имеют чётное число сторон с симметрией вращения 180°, многогранник является зоноэдром. Он является также многогранником Голдберга^[англ.] GP_IV(2,0) или {4+,3}_2,0, содержащим квадратные и шестиугольные грани.

Куб с фаской — это сумма Минковского ромбододекаэдра и куба с длиной стороны 1, когда восемь вершин ромбододекаэдра лежат в точках $(\pm 1,\pm 1,\pm 1)$ , а шесть вершин являются перестановками $(\pm 2,0,0)$ .

Куб с фаской можно построить с пиритоэдральной симметрией и прямоугольными гранями (справа). Его можно рассматривать как пентагондодекаэдр (слева) с 6 срезанными рёбрами. Такое встречается в кристаллах пирита.

Куб с фаской и связанные тела
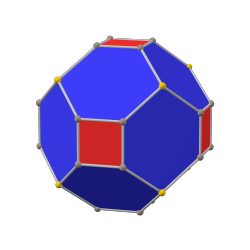Куб с фаской (канонический)	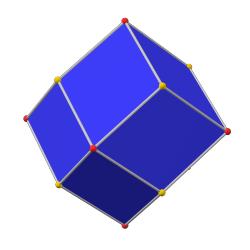ромбододекаэдр	Октаэдр с фаской
Тетракискубооктаэдр^[англ.]	кубооктаэдр	триакискубооктаэдр

Октаэдр с фаской

Октаэдр с фаской
(с равными длинами сторон)
Нотация Конвея	cO = t3daO
Граней	8 треугольников 12 шестиугольников
Рёбер	48 (2 типа)
Вершин	30 (2 типа)
Конфигурация вершины	(24) 3.6.6 (6) 6.6.6
Симметрия	O_h^[англ.], [4,3], (*432)
Двойственный многогранник	Триакискубооктаэдр
Свойства	выпуклое

В геометрии октаэдр с фаской — это выпуклый многогранник, построенный из ромбододекаэдра путём усечения 8 вершин (порядка 3).

Многогранник можно назвать усечённым ромбододекаэдром, усечением порядка 3 вершин ромбододекаэдра.

8 вершин усекаются так, что все рёбра получают равную длину. Исходные 12 ромбических граней становятся плоскими шестиугольниками, а усечённые вершины превращаются в треугольники.

Шестиугольные грани имеют равные стороны, но грани правильными не являются.

Додекаэдр с фаской

Додекаэдр с фаской
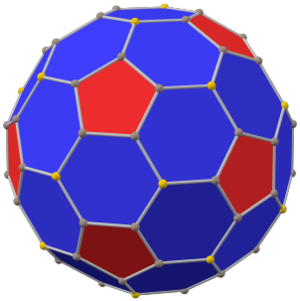(с равными длинами сторон)
Нотация Конвея tation	cD = t5daD = dk5aD
Многогранник Голдберга^[англ.]	G_V(2,0) = {5+,3}_2,0
Фуллерен	C₈₀^[1]
Вершин	12 пятиугольников 30 шестиугольников
Рёбер	120 (2 типа)
Вершин	80 (2 типа)
Конфигурация вершины	(60) 5.6.6 (20) 6.6.6
Группы симметрии	Икосаэдральная (I_h)
Двойственный многогранник	пентакисикосидодекаэдр^[англ.]
Свойства	выпуклый, грани равносторонние

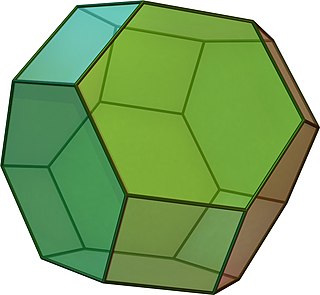
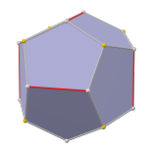
Додекаэдр с фаской — выпуклый многогранник с 80 вершинами, 120 рёбрами и 42 гранями — 30 шестиугольников и 12 пятиугольников. Многогранник строится путём снятия фаски у правильного додекаэдра. Пятиугольники уменьшаются в размерах и добавляются новые шестиугольные грани на месте всех исходных рёбер. Многогранник двойственен пентакисикосидодекаэдру^[англ.].

Многогранник не вполне правильно называется усечённым ромботриаконтаэдром. Правильнее было бы называть пятиусечённым ромботриаконтаэдром, поскольку усекаются только вершины порядка 5.

Додекаэдр с фаской и связанные тела
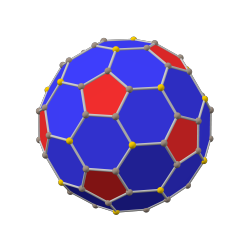додекаэдр с фаской (канонический)	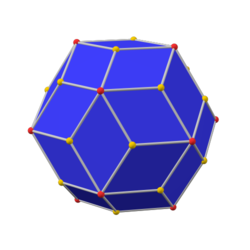ромботриаконтаэдр	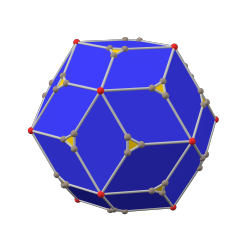икосододекаэдр с фаской (канонический)
пентакисикосидодекаэдр^[англ.]	икосододекаэдр	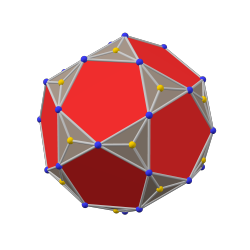триакис икосододекаэдр

Икосаэдр с фаской

Икосододекаэдр с фаской
( с равными длинами сторон)
Нотация Конвея	cI = t3daI
Граней	20 треугольников 30 шестиугольников
Рёбер	120 (2 типа)
Вершин	72 (2 типа)
Конфигурация вершины	(24) 3.6.6 (12) 6.6.6
Симметрия	I_h, [5,3], (*532)
Двойственный многогранник	триакис икосододекаэдр
Свойства	выпуклый

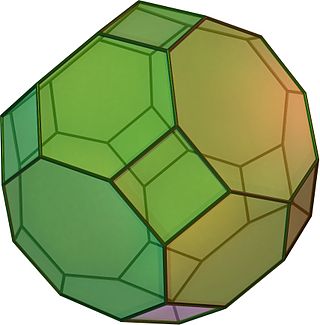
В геометрии икосаэдр с фаской — это выпуклый многогранник, построенный из ромботриаконтаэдра путём усечения 20 вершин порядка 3. Шестиугольные грани можно сделать равносторонними, но они не будут правильными.

Многогранник можно также назвать усечённым ромботриаконтаэдром, усечением вершин ромботриаконтаэдра порядка 3.

Правильные мозаики с фаской

Правильные мозаики с фаской
Квадратная мозаика, Q {4,4}	Треугольная мозаика, Δ {3,6}	Шестиугольный паркет, H {6,3}

cQ	cΔ	cH

Связь с многогранниками Голдберга

Операция снятия фаски, применённая кратно, создаёт многогранник с возрастающим числом граней, в которых рёбра предыдущего многогранника заменяются шестиугольниками. Операция снятия фаски преобразует GP(m,n) в GP(2m,2n).

Правильный многогранник GP(1,0) создаёт последовательность многогранников Голдберга^[англ.] GP(1,0), GP(2,0), GP(4,0), GP(8,0), GP(16,0)...

	GP(1,0)	GP(2,0)	GP(4,0)	GP(8,0)	GP(16,0)...
GP_IV {4+,3}	C	cC^[англ.]	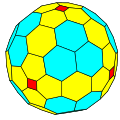ccC	cccC
GP_V {5+,3}	D	Файл:Truncated rhombic triacontahedron.svg cD^[англ.]	ccD	cccD	ccccD
GP_VI {6+,3}	H	cH	ccH	cccH	ccccH

Усечённый октаэдр или усечённый икосаэдр, GP(1,1) создаёт последовательность Голдберга GP(1,1), GP(2,2), GP(4,4), GP(8,8)....

	GP(1,1)	GP(2,2)	GP(4,4)...
GP_IV {4+,3}	tO	ctO	cctO
GP_V {5+,3}	tI	ctI	cctI
GP_VI {6+,3}	tH^[англ.]	ctH	cctH

Усечённый Тетракисгексаэдр или пентакисдодекаэдр, GP(3,0), создаёт последовательность Голдберга GP(3,0), GP(6,0), GP(12,0)...

	GP(3,0)	GP(6,0)	GP(12,0)...
GP_IV {4+,3}	tkC	ctkC	cctkC
GP_V {5+,3}	tkD^[англ.]	ctkD	cctkD
GP_VI {6+,3}	tkH	ctkH	cctkH

Многогранники и соты с фасками

Подобно операции расширения, операция фаски может быть применена в любой размерности. Для многогранников в 3-мерном пространстве операция утраивает число вершин. В более высоких размерностях создаются новые ячейки вокруг каждого ребра, при этом ячейки являются призмами, содержащими две копии исходной грани с пирамидами, добавленными к сторонам призмы.

См. также

Примечания

↑ C80 изомеры (неопр.). Дата обращения: 4 марта 2018. Архивировано из оригинала 12 августа 2014 года.

Литература

Goldberg. A class of multi-symmetric polyhedral // Tohoku Mathematical Journal. — 1937.
Joseph D. Clinton. Clinton’s Equal Central Angle Conjecture.
George W. Hart. Goldberg Polyhedra // Shaping Space / Marjorie Senechal. — 2. — Springer, 2012. — С. 125–138. — doi:10.1007/978-0-387-92714-5_9.
George W. Hart. Mathematical Impressions: Goldberg Polyhedra. — Simons Science News, 2013. — Июнь.
Antoine Deza, Michel Deza, Viatcheslav Grishukhin. Fullerenes and coordination polyhedra versus half-cube embeddings. — 1998. — С. 72 Fig. 26. Chamfered tetrahedron.
Antoine Deza, Michel Deza, Viatcheslav Grishukhin. Fullerenes and coordination polyhedra versus half-cube embeddings // Discrete Mathematics. — 1998. — Т. 192, вып. 1. — С. 41–80. — doi:10.1016/S0012-365X(98)00065-X. Архивировано 6 февраля 2007 года.