Физический маятник
Физи́ческий ма́ятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела.
Дифференциальное уравнение движения физического маятника
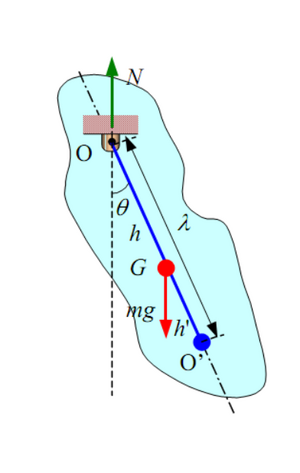
— ось подвеса;
— реакция оси подвеса;
— центр тяжести;
— центр качания;
— приведённая длина;
— угол отклонения маятника от равновесия;
— начальный угол отклонения маятника;
— масса маятника;
— расстояние от точки подвеса до центра тяжести маятника;
— ускорение свободного падения.
Момент инерции относительно оси, проходящей через точку подвеса, по теореме Штейнера:
- ,
где — момент инерции относительно оси, проходящей через центр тяжести; — эффективный радиус инерции относительно оси, проходящей через центр тяжести.
Динамическое уравнение произвольного вращения твёрдого тела:
- ,
где — суммарный момент сил, действующих на тело относительно оси вращения.
- ,
где — момент сил, вызванный силой тяжести; — момент сил, вызванный силами трения среды.
Момент, вызванный силой тяжести, зависит от угла отклонения тела от положения равновесия:
- .
Если пренебречь сопротивлением среды, дифференциальное уравнение колебаний физического маятника в поле силы тяжести:
- .
Если разделить обе части уравнения на и положить
- ,
получим:
- .
Такое уравнение аналогично уравнению колебаний математического маятника длиной . Величина называется приведённой длиной физического маятника.
Центр качания физического маятника. Теорема Гюйгенса
Центр качания — точка, в которой надо сосредоточить всю массу физического маятника, чтобы его период колебаний не изменился.
Поместим на луче, проходящем от точки подвеса через центр тяжести, точку на расстоянии от точки подвеса. Эта точка и будет центром качания маятника.
Действительно, если всю массу сосредоточить в центре качания, то центр качания будет совпадать с центром тяжести. Тогда момент инерции относительно оси подвеса будет равен , а момент силы тяжести относительно той же оси . При этом уравнение движения не изменится.
Согласно теореме Гюйгенса,
Если физический маятник подвесить за центр качания, то его период колебаний не изменится, а прежняя точка подвеса сделается новым центром качания.
Вычислим приведённую длину для нового маятника:
- .
Совпадение приведённых длин для двух случаев и доказывает утверждение, сделанное в теореме.
Период колебаний физического маятника
Наиболее общий случай
Для того, чтобы найти период колебаний физического маятника, необходимо решить уравнение качания.
Для этого умножим левую и правую часть этого уравнения на . Тогда:
- .
Интегрируя это уравнение, получаем:
- ,
где — произвольная постоянная. Её можно найти из условия, что в ситуациях, когда , должно быть ( — максимальный угол отклонения). Получаем:
Подставляем и преобразовываем получившееся уравнение:
Отделяем переменные и интегрируем это уравнение:
- .
Удобно сделать замену переменной полагая . Тогда искомое уравнение принимает вид:
Здесь — нормальный эллиптический интеграл Лежандра 1-го рода. Для периода колебаний получаем формулу:
Здесь — полный нормальный эллиптический интеграл Лежандра 1-го рода. Раскладывая его в ряд, можно получить удобную для практических вычислений формулу:
Период малых колебаний физического маятника
Если — случай малых максимальных угловых отклонений от равновесия — то так как разложение синуса в ряд Маклорена и уравнения движения переходит в уравнение гармонического осциллятора без трения:
Период колебания маятника в этом случае:
В иной формулировке: если амплитуда колебаний мала, то корень в знаменателе эллиптического интеграла приближённо равен единице. Такой интеграл легко берётся, и получается хорошо известная формула малых колебаний:
Эта формула даёт результаты приемлемой точности (ошибка менее 1 %) при углах, не превышающих 4°.
Следующий порядок приближения можно использовать с приемлемой точностью (ошибка менее 1 %) при углах отклонения до 1 радиана (≈57°):
См. также
Ссылки
- маятник — статья из Большой советской энциклопедии.








































![{\displaystyle T=2\pi {\sqrt {\frac {\lambda }{g}}}\left\{1+\left({\frac {1}{2}}\right)^{2}\sin ^{2}\left({\frac {\alpha }{2}}\right)+\left({\frac {1\cdot 3}{2\cdot 4}}\right)^{2}\sin ^{4}\left({\frac {\alpha }{2}}\right)+\dots +\left[{\frac {\left(2n-1\right)!!}{\left(2n\right)!!}}\right]^{2}\sin ^{2n}\left({\frac {\alpha }{2}}\right)+\dots \right\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aae1c69041f6957ab485b97bcbe5025dc688c47a)























