Си́мплекс или n-ме́рный тетра́эдр — геометрическая фигура, являющаяся n-мерным обобщением треугольника.
В теории графов смежной вершиной вершины v называется вершина, соединённая с v ребром. Окрестностью вершины v в графе G называется порождённый подграф графа G, состоящий из всех вершин, сопряжённых v и всех рёбер, соединяющих две такие вершины. Например, рисунок показывает граф с 6 вершинами и 7 рёбрами. Вершина 5 смежна вершинам 1, 2 и 4, но не смежна вершинам 3 и 6. Окрестность вершины 5 — это граф с тремя вершинами 1, 2 и 4, и одним ребром, соединяющим вершины 1 и 2.
В теории графов короной с 2n вершинами называется неориентированный граф с двумя наборами вершин ui и vi и рёбрами между ui и vj, если i ≠ j. Можно рассматривать корону как полный двудольный граф, из которого удалено совершенное паросочетание, как двойное покрытие двудольным графом полного графа, или как двудольный граф Кнезера Hn,1, представляющий подмножества из 1 элемента и (n − 1) элементов множества из n элементов с рёбрами между двумя подмножествами, если одно подмножество содержится в другом.
В теории графов графом без треугольников называется неориентированный граф, в котором никакие три вершины не образуют треугольник из рёбер. Графы без треугольников можно определить также как графы с кликовым числом ≤ 2, графы с обхватом ≥ 4, графы без порождённых 3-циклов, или как локально независимые графы.
В теории графов медианным графом называется неориентированный граф, в котором любые три вершины a, b, и c имеют единственную медиану — вершину m(a,b,c), которая принадлежит кратчайшим путям между каждой парой вершин a, b и c.
В теории графов рамочным графом называется вид неориентированного графа, который можно нарисовать на плоскости таким способом, что любая ограниченная грань является четырёхугольником и любая вершина с тремя и менее соседями инцидентна неограниченной грани.
Комбинаторика многогранников — это область математики, принадлежащая комбинаторике и комбинаторной геометрии и изучающая вопросы подсчёта и описания граней выпуклых многогранников.
Древесность неориентированного графа — это минимальное число лесов, на которые можно разложить рёбра. Эквивалентно это является минимальным числом остовных деревьев, которые необходимы для покрытия рёбер графа.
Фасета в геометрии — элемент многогранника или связанной геометрической структуры, как правило на единицу меньшей размерности самой структуры.
- В трёхмерном пространстве фасета многогранника — любой многоугольник, вершины которого являются вершинами многогранника, но который сам не является гранью. Огранка многогранника — нахождение и объединение фасет, которые образуют новый многогранник. Процесс является обратным образованию звёздчатой формы и может быть применён к многогранникам высоких размерностей.
- В комбинаторике многогранников и общей теории многогранников фасета многогранника размерности n — грань, имеющая размерность n−1. Фасеты можно назвать (n−1)-гранями или гипергранями. В трёхмерной геометрии они часто называются «гранями» без дальнейших уточнений.
- Фасета симплициального комплекса — максимальный симплекс, не являющейся гранью другого симплекса комплекса. Для симплициальных многогранников это совпадает с комбинаторным определением.
Конфигура́ция прямы́х — это разбиение плоскости, образованное набором прямых. Конфигурации прямых изучается в комбинаторной геометрии, а в вычислительной геометрии строятся алгоритмы для эффективного построения конфигураций.
В теории графов хорошо покрытый граф — это неориентированный граф, в котором все минимальные по включению вершинные покрытия имеют один и тот же размер. Хорошо покрытые графы определил и изучал Пламмер.
Панциклический граф — ориентированный или неориентированный граф, который содержит циклы всех возможных длин от трёх до числа вершин графа. Панциклические графы являются обобщением гамильтоновых графов, графов, которые имеют циклы максимальной возможной длины.
Плосконосый двуклиноид или сиамский додекаэдр — это трёхмерный выпуклый многогранник с двенадцатью правильными треугольниками в качестве граней. Многогранник не является правильным, поскольку в некоторых вершинах сходятся четыре грани, а в остальных — пять граней. Многогранник является двенадцатигранником, одним из восьми дельтаэдров и одним из 92 многогранников Джонсона.
В теории графов говорят, что граф G гипогамильтонов, если сам по себе граф не имеет гамильтонова цикла, но любой граф, полученный удалением одной вершины из G, является гамильтоновым.
Граф Аполлония — неориентированный граф, образованный рекурсивным процессом подразделения треугольника на три меньших треугольника. Графы Аполлония можно эквивалентно определить как планарные 3-деревья, как максимальные планарные хордальные графы, как однозначно 4-раскрашиваемые планарные графы или как графы блоковых многогранников. Графы названы именем Аполлония Пергского, изучавшего связанные построения упаковки кругов.
Однозначно раскрашиваемый граф — это k-цветный граф, допускающий только одну (правильную) k-раскраску.
Задача Конвея о 99-вершинном графе — нерешённая задача, которая спрашивает, существует ли неориентированный граф с 99 вершинами, в которых каждые две смежные вершины имеют в точности одного общего соседа и в которых две несмежные вершины имеют в точности два общих соседа. Эквивалентно, любое ребро должно быть частью единственного треугольника, а любая пара несмежных вершин должна быть на диагонали единственного 4-цикла. Джон Хортон Конвей объявил о призе в 1000 долларов тому, кто решит эту проблему.
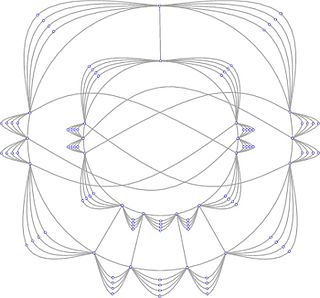
Топологический граф — представление графа на плоскости, в котором вершины графа представлены различными точками, а рёбра кривыми Жордана, соединяющими соответствующие пары точек. Точки, представляющие вершины графа, и дуги, представляющие рёбра, называются вершинами и рёбрами топологического графа. Обычно предполагается, что любые два ребра топологического графа пересекаются конечное число раз, при этом ни одно ребро не проходит через вершину и никакие два ребра не касаются друг друга. Топологический граф называется также «рисунком» графа.
Комплекс Вьеториса — Рипса, называемый также комплексом Вьеториса или Комплексом Рипса — это способ образования топологического пространства из расстояний в множестве точек. Это абстрактный симплициальный комплекс, который может быть определён из любого метрического пространства M и расстояния 
путём образования симплекса для любого конечного множества точек, которое имеет диаметр, не превосходящий . То есть, это семейство конечных подмножеств метрического пространства M, в котором мы понимаем подмножество из k точек как (k − 1)-мерный симплекс (ребро для двух точек, треугольник для трёх, тетраэдр для четырёх и т.д.). Если же конечное множество S обладает свойством, что расстояние между любой парой точек в S не превосходит , то мы включаем S в качестве симплекса в комплекс.
