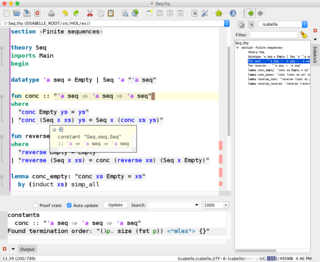
Формальная верификация

Формальная верификация или формальное доказательство — формальное доказательство соответствия или несоответствия предмета верификации его формальному описанию. Предметом выступают алгоритмы, программы и другие доказательства.

Из-за рутинности даже простой формальной верификации и теоретической возможности их полной автоматизации под формальной верификацией обычно подразумевают автоматическую верификацию с помощью программы.

Тестирование программного обеспечения не может доказать, что система, алгоритм или программа не содержит никаких ошибок и дефектов и удовлетворяет определённому свойству. Это может сделать формальная верификация.

Формальная верификация может использоваться для проверки таких систем, как программное обеспечение, представленное в виде исходных текстов, криптографические протоколы, комбинаторные логические схемы, цифровые схемы с внутренней памятью.

Верификация представляет собой формальное доказательство на абстрактной математической модели системы, в предположении о том, что соответствие между математической моделью и природой системы считается изначально заданным. Например, по построению модели либо математического анализа и доказательства правильности алгоритмов и программ.

Примерами математических объектов, часто используемых для моделирования и формальной верификации программ и систем являются:

• формальная семантика языков программирования, например операционная семантика^[англ.], денотационная семантика^[англ.], аксиоматическая семантика^[англ.] (логика Хоара), математическая семантика программ
• теории и системы типов — в первую очередь, системы с зависимыми типами (см. лямбда-куб)
• логика разделения (расширение логики Хоара)
• конечный автомат
• помеченная модель состояний и переходов
• сеть Петри
• временной автомат
• гибридный автомат
• исчисление процессов
• структурированные алгоритмы
• структурированные программы

Существуют следующие подходы к формальной верификации:

• формальная семантика языков программирования
• написание программ, которые верны по построению (см. зависимый тип, лямбда-куб, параметричность^[англ.])
• проверка моделей (model checking)
• логический вывод (logical inference)
• символьное выполнение^[англ.]
• абстрактная интерпретация^[англ.]
• систематический анализ алгоритмов и программ
• технологии доказательного программирования

Доказательное программирование — использовавшаяся в 1980-х годах в академических кругах технология разработки программ для ЭВМ с доказательствами правильности — доказательствами отсутствия ошибок в программах (понимая, в рамках данной теории, ошибки как несоответствия между задуманным алгоритмом и фактическим алгоритмом, реализуемым программой).

Доказательство может быть автоматизировано полностью лишь для очень небольшого круга простых теорий, поэтому важное значение получает его автоматическая проверка и для этого преобразование к проверяемому виду. ^[] Значительное количество практически важных задач, в том числе, например, задача остановки, является алгоритмически неразрешимыми.

Для поддержания строгости при проверке доказательства верификатором следует проверить ещё и верификатор, для чего нужен ещё один верификатор и так далее. Получившуюся бесконечную цепь верификаторов можно было бы свернуть, построив верифицирующий себя верификатор, обладающий способностью развернуться до применимого на практике. ^[]

Код аутентификации HMAC от OpenSSL из 134 строк на языке C был верифицирован с использованием 2832 строк на Coq.

Еще одним примером является файловая система FSCQ. Код и его верификация выполнялись на Coq, занимая 31 тысяч строк доказательства и кода в сумме. Для сравнения, непроверенная файловая система написана на C и занимает всего 3 тысяч строк. Несмотря на то что первоначальные работы, включая создание логического каркаса для Coq, требовали нескольких человеко-лет, эксперименты выявили поэтапное снижение стоимости при внесении изменений в код и доказательство.^[1]

• Формальная верификация криптографических протоколов
• Контрактное программирование
• Логика Хоара
• Тестирование программного обеспечения
• Обеспечение безопасности посредством языка (англ. Language-based security)

• А. М. Миронов. Методы верификации программ  (неопр.).
• А. С. Камкин. Введение в формальные методы верификации программ: учебное пособие  (неопр.).
• Lathouwers, Sophie; Zaytsev, Vadim (2022). "Modelling Program Verification Tools for Software Engineers". Proceedings of the 25th International Conference on Model Driven Engineering Languages and Systems. MODELS '22. Montreal, Quebec, Canada: Association for Computing Machinery. pp. 98—108. doi:10.1145/3550355.3552426. ISBN 9781450394666.

• Sophie Lathouwers, Vadim Zaytsev. ProVerB: Program Verification Book (англ.). (один из вариантов классификации и большой список средств формальной верификации)