
Вероя́тность — степень возможности наступления некоторого события. Когда основания для того, чтобы какое-нибудь возможное событие произошло в действительности, перевешивают противоположные основания, то это событие называют вероятным, в противном случае — маловероятным или невероятным. Перевес положительных оснований над отрицательными, и наоборот, может быть в различной степени, вследствие чего вероятность бывает большей либо меньшей. Поэтому часто вероятность оценивается на качественном уровне, особенно в тех случаях, когда более или менее точная количественная оценка невозможна или крайне затруднена. Возможны различные градации «уровней» вероятности.
Математи́ческое ожида́ние — понятие в теории вероятностей, означающее среднее значение случайной величины. В случае непрерывной случайной величины подразумевается взвешивание по плотности распределения. Математическое ожидание случайного вектора равно вектору, компоненты которого равны математическим ожиданиям компонентов случайного вектора.
Комбинато́рика — раздел математики, посвящённый решению задач, связанных с выбором и расположением элементов некоторого множества в соответствии с заданными правилами. Каждое такое правило определяет некоторую выборку из элементов исходного множества, которая называется комбинаторной конфигурацией. Простейшими примерами комбинаторных конфигураций являются перестановки, сочетания и размещения.
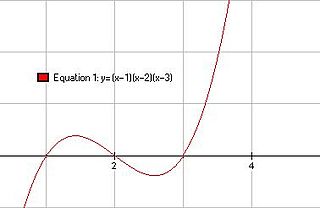
Корень многочлена


В теории алгоритмов классом сложности BPP называется класс предикатов, быстро вычислимых и дающих ответ с высокой вероятностью. Задачи, решаемые вероятностными методами и лежащие в BPP, возникают на практике очень часто.
Усло́вная вероя́тность — вероятность наступления события  при условии, что событие
при условии, что событие  произошло. Вероятность события
произошло. Вероятность события  , вычисленную в предположении, что о результате эксперимента уже что-то известно, мы будем обозначать через
, вычисленную в предположении, что о результате эксперимента уже что-то известно, мы будем обозначать через  . Например, вероятность того, что у какого-то человека будет кашель в произвольный день,
. Например, вероятность того, что у какого-то человека будет кашель в произвольный день,  . Но если мы знаем или предполагаем, что у человека простуда, тогда у него гораздо больше шансов начать кашлять. Таким образом, условная вероятность кашля у любого человека при условии, что он простужен, выше
. Но если мы знаем или предполагаем, что у человека простуда, тогда у него гораздо больше шансов начать кашлять. Таким образом, условная вероятность кашля у любого человека при условии, что он простужен, выше  .
.

Распределе́ние Берну́лли в теории вероятностей и математической статистике — дискретное распределение вероятностей, моделирующее случайный эксперимент произвольной природы, при заранее известной вероятности успеха или неудачи.

Закон больших чисел (ЗБЧ) в теории вероятностей — принцип, описывающий результат выполнения одного и того же эксперимента много раз. Согласно закону, среднее значение конечной выборки из фиксированного распределения близко к математическому ожиданию этого распределения.

Парадо́кс дней рожде́ния — утверждение, состоящее в том, что в группе, состоящей из 23 или более человек, вероятность совпадения дней рождения хотя бы у двух людей превышает 50 %. Например, если в классе 23 ученика или более, то более вероятно то, что у какой-то пары одноклассников дни рождения придутся на один день, чем то, что у каждого будет свой неповторимый день рождения. Впервые эта задача была рассмотрена Рихардом Мизесом в 1939 году.
Соотноше́ние Безу́ — представление наибольшего общего делителя целых чисел в виде их линейной комбинации с целыми коэффициентами.
Правило Стёрджеса — эмпирическое правило определения оптимального количества интервалов, на которые разбивается наблюдаемый диапазон изменения случайной величины при построении гистограммы плотности её распределения. Названо по имени американского статистика Герберта Стёрджеса.

История теории вероятностей отмечена многими уникальными особенностями. Прежде всего, в отличие от появившихся примерно в то же время других разделов математики, у теории вероятностей по существу не было античных или средневековых предшественников, она целиком — создание Нового времени. Долгое время теория вероятностей считалась чисто опытной наукой и «не совсем математикой», её строгое обоснование было разработано только в 1929 году, то есть даже позже, чем аксиоматика теории множеств (1922). В наши дни теория вероятностей занимает одно из первых мест в прикладных науках по широте своей области применения; «нет почти ни одной естественной науки, в которой так или иначе не применялись бы вероятностные методы».
Логическая вероятность — логическое отношение между двумя предложениями, степень подтверждения гипотезы H свидетельством E.

Байесовская статистика — теория в области статистики, основанная на байесовской интерпретации вероятности, когда вероятность отражает степень доверия событию, которая может измениться, когда будет собрана новая информация, в отличие от фиксированного значения, основанного на частотном подходе. Степень доверия может основываться на априорных знаниях о событии, таких как результаты предыдущих экспериментов или личное доверие событию. Это отличается от ряда других интерпретаций вероятности, таких как частотная интерпретация, которая рассматривает вероятность как предел относительной частоты выпадения события после большого числа испытаний.












































