Э́ллипс — замкнутая плоская кривая, исторически определённая как одно из конических сечений . Название эллипсу дал Аполлоний Пергский в своей «Конике».

Гамма-функция — математическая функция. Была введена Леонардом Эйлером, а своим обозначением гамма-функция обязана Лежандру.

Преобразование Фурье́ — операция, сопоставляющая одной функции вещественной переменной другую функцию вещественной переменной. Эта новая функция описывает коэффициенты («амплитуды») при разложении исходной функции на элементарные составляющие — гармонические колебания с разными частотами.

Теле́сный у́гол — часть пространства, которая является объединением всех лучей, выходящих из данной точки и пересекающих некоторую поверхность. Частными случаями телесного угла являются трёхгранные и многогранные углы. Границей телесного угла является некоторая коническая поверхность. Обозначается телесный угол обычно буквой Ω.

Циссоида Диокла — плоская алгебраическая кривая третьего порядка. В декартовой системе координат, где ось абсцисс направлена по  , а ось ординат по
, а ось ординат по  , на отрезке
, на отрезке  , как на диаметре строится вспомогательная окружность. В точке
, как на диаметре строится вспомогательная окружность. В точке  проводится касательная
проводится касательная  . Из точки
. Из точки  проводится произвольная прямая
проводится произвольная прямая  , которая пересекает окружность в точке
, которая пересекает окружность в точке  и касательную в точке
и касательную в точке  . От точки
. От точки  , в направлении точки
, в направлении точки  , откладывается отрезок
, откладывается отрезок  , длина которого равна длине отрезка
, длина которого равна длине отрезка  . При вращении линии
. При вращении линии  вокруг точки
вокруг точки  , точка
, точка  описывает линию, которая называется Циссоида Диокла. Две ветви этой линии на рис. 1 показаны синим и красным цветами.
описывает линию, которая называется Циссоида Диокла. Две ветви этой линии на рис. 1 показаны синим и красным цветами.

Де́льта-фу́нкция — обобщённая функция, которая позволяет записать точечное воздействие, а также пространственную плотность физических величин, сосредоточенных или приложенных в одной точке.
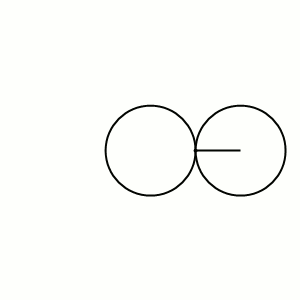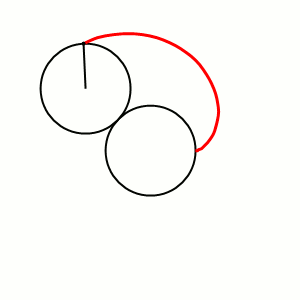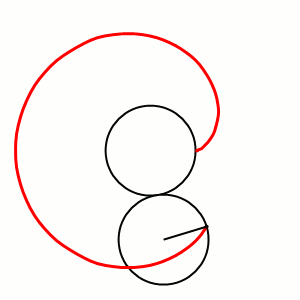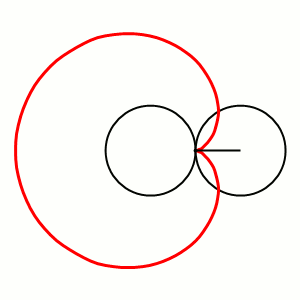
Кардио́ида, или сердцеви́дная крива́я — плоская линия, которая описывается фиксированной точкой окружности, катящейся по неподвижной окружности с таким же радиусом. Получила своё название из-за схожести своих очертаний со стилизованным изображением сердца.

Распределе́ние Ма́ксвелла — общее наименование нескольких распределений вероятности, которые описывают статистическое поведение параметров частиц идеального газа. Вид соответствующей функции плотности вероятности диктуется тем, какая величина: скорость частицы, проекция скорости, модуль скорости, энергия, импульс и т. д. — выступает в качестве непрерывной случайной величины. В ряде случаев распределение Максвелла может быть выражено как дискретное распределение по множеству уровней энергии.
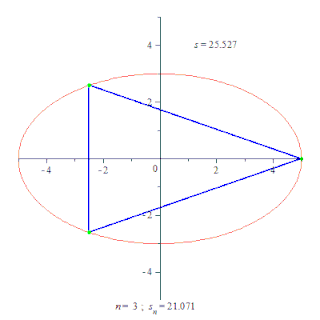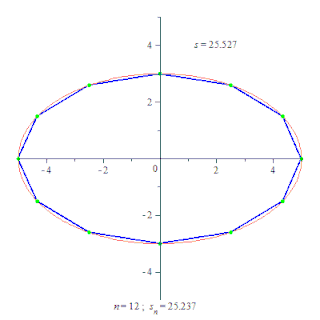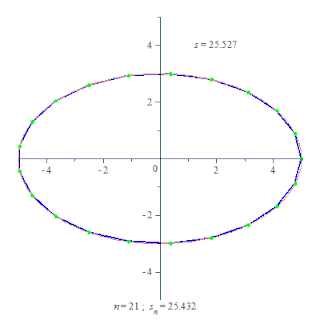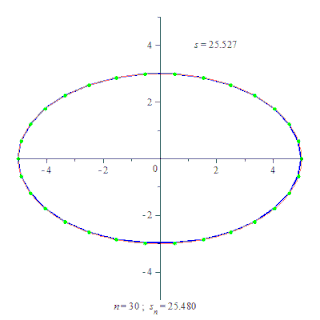
Длина́ криво́й — числовая характеристика протяжённости этой кривой. Исторически вычисление длины кривой называлось спрямлением кривой.

Фу́нкции Бе́сселя в математике — семейство функций, являющихся каноническими решениями дифференциального уравнения Бесселя:


Закон Био́—Савара—Лапла́са — физический закон для определения вектора индукции магнитного поля, порождаемого постоянным электрическим током. Был установлен экспериментально в 1820 году Био и Саваром и сформулирован в общем виде Лапласом. Лаплас показал также, что с помощью этого закона можно вычислить магнитное поле движущегося точечного заряда.
Эллипти́ческий интегра́л — некоторая функция  над полем действительных или комплексных чисел, которая может быть формально представлена в следующем виде:
над полем действительных или комплексных чисел, которая может быть формально представлена в следующем виде:
 ,
,
Интегральная формула Коши — соотношение для голоморфных функций комплексного переменного, связывающее значение функции в точке с её значениями на контуре, окружающем точку.
Гипергеометри́ческая фу́нкция — одна из специальных функций. Определяется внутри круга  как сумма гипергеометрического ряда
как сумма гипергеометрического ряда

Преобразование Меллина — преобразование, которое можно рассматривать как мультипликативную версию двустороннего преобразования Лапласа. Это интегральное преобразование тесно связано с теорией рядов Дирихле и часто используется в теории чисел и в теории асимптотических разложений. Преобразование Меллина тесно связано с преобразованием Лапласа и преобразованием Фурье, а также теорией гамма-функций и теорией смежных специальных функций.

Карл Юхан Мальмстен — шведский математик и политический деятель. Известен своими ранними работами по комплексному анализу, теории некоторых специальных функций, а также как сооснователь математического журнала Acta Mathematica.

Сфери́ческий сегме́нт — поверхность, часть сферы, отсекаемая от неё некоторой плоскостью. Плоскость отсекает два сегмента: меньший сегмент называется также сферическим кругом. Если секущая плоскость проходит через центр сферы, то высота обоих сегментов равна радиусу сферы, и каждый из таких сферических сегментов называют полусферой.