Формула конечных приращений

Формула конечных приращений, или теорема Лагра́нжа о среднем значении, утверждает, что если функция ${\displaystyle f}$ непрерывна на отрезке ${\displaystyle [a;b]}$ и дифференцируема в интервале ${\displaystyle (a;b)}$, то найдётся такая точка ${\displaystyle c\in (a;b)}$, что

${\displaystyle {\frac {f(b)-f(a)}{b-a}}=f'(c)}$.

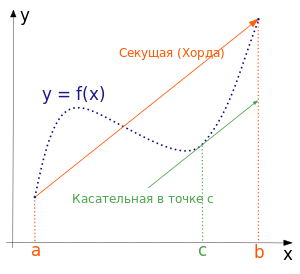
Геометрически это можно переформулировать так: на отрезке ${\displaystyle [a;b]}$ найдётся внутренняя точка, в которой касательная параллельна хорде, проходящей через точки графика, соответствующие концам отрезка.

Механическое истолкование: Пусть ${\displaystyle f(t)}$ — расстояние точки в момент ${\displaystyle t}$ от начального положения. Тогда ${\displaystyle f(b)-f(a)}$ есть путь, пройденный с момента ${\displaystyle t=a}$ до момента ${\displaystyle t=b}$, отношение ${\displaystyle {\frac {f(b)-f(a)}{b-a}}}$ — средняя скорость за этот промежуток. Значит, если скорость тела определена в любой момент времени ${\displaystyle t\in (a,b)}$, то в некоторый момент она будет равна своему среднему значению на этом участке.

Название «конечные приращения» объясняется, что, если в формуле ${\displaystyle f(b)-f(a)=f'(c)(b-a)}$, левая часть ${\displaystyle \Delta y=f(b)-f(a)}$ есть приращение функции, а в правой части присутствует приращение аргумента ${\displaystyle \Delta x=b-a}$. В этих обозначениях формулу можно переписать как

${\displaystyle \Delta y=f'(c)\Delta x,}$

что в свою очередь уже очень похоже на определение дифференциала:

${\displaystyle dy=f'(x)dx}$

с той лишь разницей, что в формуле конечных приращений у нас дана формула нахождения истинного приращения ${\displaystyle \Delta y}$, но через производную ${\displaystyle f'(c)}$ в точке ${\displaystyle c}$, которая находится где-то между ${\displaystyle a}$ и ${\displaystyle b}$. Если же в формуле ${\displaystyle \Delta y=f'(c)\Delta x}$ устремить ${\displaystyle \Delta x}$ к нулю, то в пределе мы получим ${\displaystyle dy=f'(x)dx}$^[1].

• Теорема Лагранжа иногда может быть применена при раскрытии неопределённостей для нахождения пределов.

Теорема Лагранжа о конечных приращениях — одна из самых важных, узловая теорема во всей системе дифференциального исчисления. Она имеет массу приложений в вычислительной математике, и главнейшие теоремы математического анализа также являются её следствиями.

• Дифференцируемая на отрезке функция с производной, равной нулю, есть константа.

Доказательство. Для любых ${\displaystyle x}$ и ${\displaystyle y}$ существует точка ${\displaystyle c}$, такая что ${\displaystyle f(y)-f(x)=f'(c)(y-x)=0}$.

Значит, при всех ${\displaystyle x}$ и ${\displaystyle y}$ верно равенство ${\displaystyle f(y)=f(x)}$.

Замечание. Аналогично доказывается следующий важный критерий монотонности для дифференцируемых функций: Дифференцируемая функция ${\displaystyle f(x)}$ возрастает/убывает на отрезке ${\displaystyle [a,b]}$ тогда и только тогда, когда её производная ${\displaystyle f'(x)}$ на этом отрезке неотрицательна/неположительна. При этом строгая положительность/отрицательность производной влечёт строгую монотонность функции ${\displaystyle f(x)}$.

• Формула Тейлора с остаточным членом в форме Лагранжа). Если функция ${\displaystyle f}$ дифференцируема ${\displaystyle n}$ раз в окрестности точки ${\displaystyle x}$, то для малых ${\displaystyle h}$ (то есть тех, для которых отрезок ${\displaystyle [x,x+h]}$ лежит в указанной окрестности) справедлива формула Тейлора:

${\displaystyle f(x+h)=f(x)+f'(x)h+f''(x){\frac {h^{2}}{2}}+...+f^{(n-1)}(x){\frac {h^{n-1}}{(n-1)!}}+f^{(n)}(x+\theta h){\frac {h^{n}}{n!}}}$

где ${\displaystyle \theta }$ — некоторое число из интервала ${\displaystyle (0,1)}$.

Замечание. Данное следствие является в то же время и обобщением. При ${\displaystyle n=1}$ из него получается сама теорема Лагранжа о конечных приращениях.

• Если функция ${\displaystyle n}$ переменных ${\displaystyle f(x_{1},x_{2},\dots ,x_{n})}$ дважды дифференцируема в окрестности точки О и все её вторые смешанные производные непрерывны в точке О, тогда в этой точке справедливо равенство:

${\displaystyle {\frac {\partial ^{2}f}{\partial x_{i}\partial x_{j}}}={\frac {\partial ^{2}f}{\partial x_{j}\partial x_{i}}}}$

Доказательство для ${\displaystyle n=2}$. Зафиксируем значения ${\displaystyle \Delta x}$ и ${\displaystyle \Delta y}$ и рассмотрим разностные операторы

${\displaystyle \Delta _{x}:f(x,y)\rightarrow {\frac {f(x+\Delta x,y)-f(x,y)}{\Delta x}}}$ и ${\displaystyle \Delta _{y}:f(x,y)\rightarrow {\frac {f(x,y+\Delta y)-f(x,y)}{\Delta y}}}$.

По теореме Лагранжа существуют числа ${\displaystyle \theta _{1},\theta _{2}\in (0,1)}$, такие что

${\displaystyle \Delta _{y}\Delta _{x}f(x,y)=\Delta _{y}{\frac {\partial f}{\partial x}}(x+\theta _{1}\Delta x,y)={\frac {\partial }{\partial y}}{\frac {\partial f}{\partial x}}(x+\theta _{1}\Delta x,y+\theta _{2}\Delta y)\rightarrow {\frac {\partial }{\partial y}}{\frac {\partial f}{\partial x}}(x,y)}$

при ${\displaystyle (\Delta x,\Delta y)\rightarrow 0}$ в силу непрерывности вторых производных функции ${\displaystyle f(x,y)}$.

Аналогично доказывается, что ${\displaystyle \Delta _{x}\Delta _{y}f(x,y)\rightarrow {\frac {\partial }{\partial x}}{\frac {\partial f}{\partial y}}(x,y)}$.

Но так как ${\displaystyle \Delta _{y}\Delta _{x}f(x,y)=\Delta _{x}\Delta _{y}f(x,y)}$, (что проверяется непосредственно), то эти пределы совпадают.

Замечание. Следствием этой формулы является тождество ${\displaystyle d^{2}=0}$ для оператора внешнего дифференциала, определённого на дифференциальных формах.

• Формула Ньютона — Лейбница. Если функция ${\displaystyle f(x)}$ дифференцируема на отрезке ${\displaystyle [a,b]}$ и её производная интегрируема по Риману на этом отрезке, то справедлива формула: ${\displaystyle \int \limits _{a}^{b}f'(x)dx=f(b)-f(a)}$.

Доказательство. Пусть ${\displaystyle T}$ — произвольное разбиение ${\displaystyle a=x_{0}<x_{1}<x_{2}<...<x_{n}=b}$ отрезка ${\displaystyle [a,b]}$. Применяя теорему Лагранжа, на каждом из отрезков ${\displaystyle [x_{k-1},x_{k}]}$ найдём точку ${\displaystyle \xi _{k}}$ такую, что ${\displaystyle f'(\xi _{k})(x_{k}-x_{k-1})=f(x_{k})-f(x_{k-1})}$.

Суммируя эти равенства, получим: ${\displaystyle \sum \limits _{k=1}^{n}f'(\xi _{k})(x_{k}-x_{k-1})=\sum \limits _{k=1}^{n}(f(x_{k})-f(x_{k-1}))=f(b)-f(a)}$

Слева стоит интегральная сумма Римана для интеграла ${\displaystyle \int \limits _{a}^{b}f'(x)dx}$ и заданного отмеченного разбиения. Переходя к пределу по диаметру разбиения, получим формулу Ньютона-Лейбница.

Замечание. Следствием (и обобщением) формулы Ньютона-Лейбница является формула Стокса, а следствием формулы Стокса является интегральная теорема Коши — основная теорема теории аналитических функций (ТФКП).

• Теорема об оценке конечных приращений. Пусть отображение ${\displaystyle F:\Omega \rightarrow \mathbb {R} ^{m}}$ непрерывно дифференцируемо в выпуклой компактной области ${\displaystyle \Omega }$ пространства ${\displaystyle \mathbb {R} ^{n}}$. Тогда ${\displaystyle |F(y)-F(x)|\leq \sup \limits _{\xi \in \Omega }|DF(\xi )|\cdot |y-x|}$.

Замечание. Без использования теоремы об оценке конечных приращений не обходятся доказательства таких теорем, как теорема об обратном отображении, теорема о неявной функции, теорема о существовании и единственности решения задачи Коши для обыкновенных дифференциальных уравнений.

• Лагранж, Жозеф Луи
• Теорема Коши — расширенный вариант этой теоремы.