
Гамма-функция — математическая функция. Была введена Леонардом Эйлером, а своим обозначением гамма-функция обязана Лежандру.
Когере́нтность — в физике скоррелированность (согласованность) нескольких колебательных или волновых процессов во времени, проявляющаяся при их сложении. Колебания когерентны, если разность их фаз постоянна во времени, и при сложении колебаний получается колебание той же частоты.
Ниже приведён список интегралов от экспоненциальной функции. В списке везде опущена константа интегрирования.

Фу́нкции Бе́сселя в математике — семейство функций, являющихся каноническими решениями дифференциального уравнения Бесселя:

Эллипти́ческий интегра́л — некоторая функция  над полем действительных или комплексных чисел, которая может быть формально представлена в следующем виде:
над полем действительных или комплексных чисел, которая может быть формально представлена в следующем виде:
 ,
,
Гипергеометри́ческая фу́нкция — одна из специальных функций. Определяется внутри круга  как сумма гипергеометрического ряда
как сумма гипергеометрического ряда


Сферические функции представляют собой угловую часть семейства ортогональных решений уравнения Лапласа, записанную в сферических координатах. Они широко используются для изучения физических явлений в пространственных областях, ограниченных сферическими поверхностями и при решении физических задач, обладающих сферической симметрией. Сферические функции имеют большое значение в теории дифференциальных уравнений в частных производных и теоретической физике, в частности в задачах расчёта электронных орбиталей в атоме, гравитационного поля геоида, магнитного поля планет и интенсивности реликтового излучения.

Модифици́рованные фу́нкции Бе́сселя — это функции Бесселя от чисто мнимого аргумента.
В математике Дзета-функция Гурвица, названная в честь Адольфа Гурвица, — это одна из многочисленных дзета-функций, являющихся обобщениями дзета-функции Римана. Формально она может быть определена степенным рядом для комплексных аргументов s, при Re(s) > 1, и q, Re(q) > 0:

Пропагатор в квантовой механике и квантовой теории поля (КТП) — функция, характеризующая распространение релятивистского поля от одного акта взаимодействия до другого. Эта функция определяет амплитуду вероятности перемещения частицы из одного места пространства в другое за заданный промежуток времени или перемещения частицы с определённой энергией и импульсом. Для расчёта частоты столкновений в КТП используются виртуальные частицы, представленные в диаграммах Фейнмана пропагаторами, вносят свой вклад в вероятность рассеяния, описываемого соответствующей диаграммой. Их также можно рассматривать как оператор, обратный волновому оператору, соответствующему частице, и поэтому их часто называют (причинными) функциями Грина.
Функция Вебера — неэлементарная функция, которая является частным решением неоднородного уравнения Бесселя:


Функция Струве — неэлементарная функция, которая является частным решением неоднородного уравнения Бесселя:

Функция Бурже — неэлементарная фу́нкция, которая является интегральным обобщением бесселевых функций. Введена Ж. Бурже в 1861 г. Она определяется следующим образом:

Функции Кельвина — группа бесселевых функций. Каждая их пара представляют решения дифференциального уравнения:

Статическая изотропная метрика — это метрика, определяющая статическое изотропное гравитационное поле. Частным случаем этой метрики является метрика Шварцшильда, на случай пустого пространства-времени.

Тета-функции — это специальные функции от нескольких комплексных переменных. Они играют важную роль во многих областях, включая теории абелевых многообразий, пространства модулей и квадратичных форм. Они применяются также в теории солитонов. После обобщения к алгебре Грассмана функции появляются также в квантовой теории поля.

Сфери́ческий сегме́нт — поверхность, часть сферы, отсекаемая от неё некоторой плоскостью. Плоскость отсекает два сегмента: меньший сегмент называется также сферическим кругом. Если секущая плоскость проходит через центр сферы, то высота обоих сегментов равна радиусу сферы, и каждый из таких сферических сегментов называют полусферой.
Векторными сферическими гармониками являются векторные функции, преобразующиеся при вращениях системы координат так же, как скалярные сферические функции с теми же индексами, или определенные линейные комбинации таких функций.
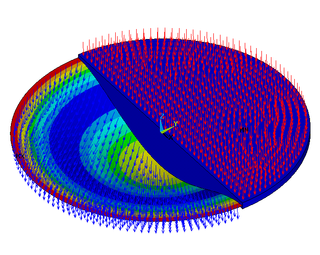
Изгиб пластин в теории упругости относится к расчёту деформаций в пластинах, под действием перпендикулярных к плоскости пластины внешних сил и моментов. Величину отклонения можно определить, решив дифференциальные уравнения соответствующей теории пластин в зависимости от допущений на малость тех или иных параметров. По этим прогибам можно рассчитать напряжения в пластине. При известных напряжениях можно использовать теорию разрушения, чтобы определить, нарушение целостности плиты при данной нагрузке. Деформация пластины является функцией двух координат, поэтому теория пластин формулируется в общем случае в терминах дифференциальных уравнений в двумерном пространстве. Также считается, что пластина изначально имеет плоскую форму.




























