Э́ллипс — замкнутая плоская кривая, исторически определённая как одно из конических сечений . Название эллипсу дал Аполлоний Пергский в своей «Конике».
Выпуклая функция — функция, надграфик или подграфик которой является выпуклым множеством.
Численное интегрирование — вычисление значения определённого интеграла. Под численным интегрированием понимают набор численных методов для нахождения значения определённого интеграла.
Экстре́мум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. В математическом анализе выделяют также понятие локальный экстремум .
Губка Менгера — геометрический фрактал, один из трёхмерных аналогов ковра Серпинского.
Критической точкой дифференцируемой функции 
называется точка, в которой её дифференциал обращается в нуль. Это условие эквивалентно тому, что в данной точке все частные производные первого порядка обращаются в нуль, геометрически оно означает, что касательная гиперплоскость к графику функции горизонтальна. В простейшем случае n=1 это значит, что производная 
в данной точке равна нулю. Это условие является необходимым для того, чтобы внутренняя точка области могла быть точкой локального минимума или максимума дифференцируемой функции.
Точка перегиба — точка плоской кривой, в которой её ориентированная кривизна меняет знак. Если кривая является графиком функции, то в этой точке выпуклая часть функции отделяется от вогнутой.
Оптимизация — задача нахождения экстремума целевой функции в некоторой области конечномерного векторного пространства, ограниченной набором линейных и/или нелинейных равенств или неравенств.
Градиентный спуск, метод градиентного спуска — численный метод нахождения локального минимума или максимума функции с помощью движения вдоль градиента, один из основных численных методов современной оптимизации.
Билине́йная интерполя́ция — в вычислительной математике — обобщение линейной интерполяции одной переменной для функций двух переменных.
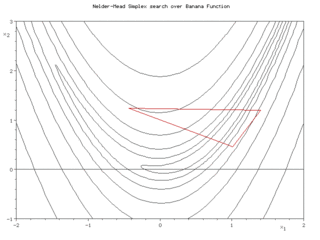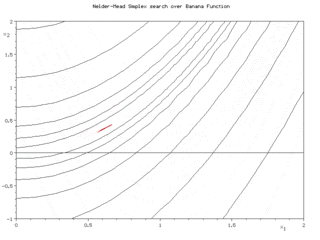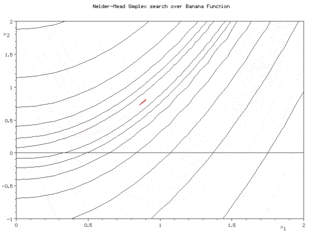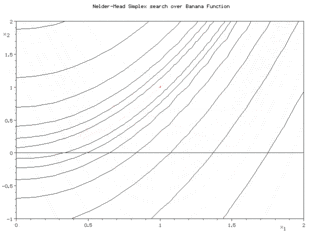
Метод Нелдера — Мида, также известный как метод деформируемого многогранника и симплекс-метод, — метод безусловной оптимизации функции от нескольких переменных, не использующий производной функции, а поэтому легко применим к негладким и/или зашумлённым функциям.
Дифференциа́льная эволю́ция — метод многомерной математической оптимизации, относящийся к классу стохастических алгоритмов оптимизации и использующий некоторые идеи генетических алгоритмов.
Функция Розенброка — невыпуклая функция, используемая для оценки производительности алгоритмов оптимизации, предложенная Ховардом Розенброком в 1960 году. Считается, что поиск глобального минимума для данной функции является нетривиальной задачей.
Многокритериальная оптимизация, или программирование — это процесс одновременной оптимизации двух или более конфликтующих целевых функций в заданной области определения.
Алгоритм Бройдена — Флетчера — Гольдфарба — Шанно (BFGS) — итерационный метод численной оптимизации, предназначенный для нахождения локального максимума/минимума нелинейного функционала без ограничений.
В теории оптимизации допустимая область, допустимое множество, пространство поиска или пространство решений — это множество всех возможных точек задачи оптимизации, которые удовлетворяют ограничениям задачи. Эти ограничения могут включать неравенства, равенства и требование целочисленности решения . Область допустимых решений является начальной областью поиска кандидатов в решение задачи, и эта область во время поиска может сужаться.
Нелинейная регрессия — это вид регрессионного анализа, в котором экспериментальные данные моделируются функцией, являющейся нелинейной комбинацией параметров модели и зависящей от одной и более независимых переменных. Данные аппроксимируются методом последовательных приближений.
Выпуклое программирование — это подобласть математической оптимизации, которая изучает задачу минимизации выпуклых функций на выпуклых множествах. В то время как многие классы задач выпуклого программирования допускают алгоритмы полиномиального времени, математическая оптимизация в общем случае NP-трудна.
В математике множество уровня вещественной функции f от n вещественных переменных — это множество вида
