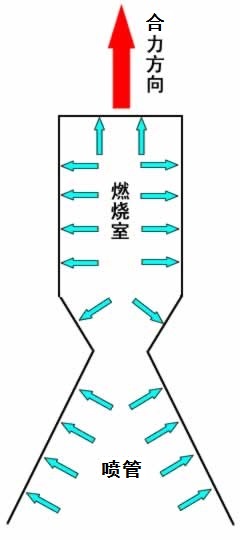
Характеристическая скорость орбитального манёвра
Характеристи́ческая ско́рость орбита́льного манёвра — в астродинамике и ракетодинамике изменение скорости космического аппарата, которое необходимо для выполнения орбитального манёвра (изменения траектории). Является скаляром и имеет размерность скорости. Обозначается в формулах как Δv (дельта-v; произносится как де́льта-вэ́). В случае реактивного двигателя изменение скорости достигается путём выброса рабочего тела для производства реактивной тяги, которая и ускоряет корабль в космосе.
Сумма́рная характеристи́ческая ско́рость — сумма характеристических скоростей всех манёвров, необходимых для поддержания работоспособности космического аппарата или системы (орбитальной группировки) на протяжении всего периода эксплуатации[1].
Определение
где
Особые случаи
При отсутствии внешних сил (вакуум, гравитация небесных тел пренебрежимо мала, электромагнитные поля слабы):
где a — ускорение. Когда тяга приложена в постоянном направлении (без рысканья и тангажа), уравнение упрощается до
то есть просто до изменения скорости (относительно точки отчета в инерционной системе).
Орбитальные манёвры
Орбитальные манёвры, как правило, выполняются выбросом из ракетного двигателя рабочего тела (газов) для создания противосилы, действующей на корабль. Значение этой силы равно
где
- Vи — скорость истечения газа (рабочего тела),
- — массовый расход рабочего тела.
Ускорение (производная от скорости) корабля, вызванное этой силой, равно
где m — масса корабля.
Меняя переменную уравнения с времени t на массу корабля m, получаем:
Если считать скорость истечения газа Vи постоянной и не зависящей от остатков топлива, времени работы двигателя, это уравнение интегрируется в форму
которая и есть формула Циолковского.
Если, к примеру, 25 % начальной массы корабля — это топливо со скоростью истечения газов в районе 2100 м/с (обычное значение для гидразина), то достижимое для корабля полное изменение скорости равно:
- м/с = 604 м/с.
Все приведённые формулы хорошо сходятся с реальностью для импульсных манёвров, характерных для химических реактивных двигателей (то есть с реакцией окисления горючего). Но для двигателей с малой тягой (например, ионных двигателей), а также двигателей, использующих электрические поля, солнечный ветер и т. п., эти упрощенные расчеты менее точны, особенно если периоды работы двигателей (создания тяги) превышают несколько часов.
Также для химических двигателей с большой тягой действует эффект Оберта — включение ракетного двигателя при движении с высокой скоростью создаёт больше полезной энергии, чем такой же ракетный двигатель при медленной скорости. При движении с высокой скоростью топливо имеет больше кинетической энергии (она может даже превысить потенциальную химическую энергию), и эта энергия может использоваться для получения большей механической мощности.
Дельта-v для разных целей
Выход на земную орбиту
Запуск на низкую околоземную орбиту (НОО) с поверхности Земли требует дельта-v около 7,8 км/с плюс от 1,5 до 2,0 км/с, затрачиваемых на преодоление сопротивления атмосферы, гравитационные потери и манёвры по тангажу. Надо учитывать, что при запуске с поверхности Земли в восточном направлении к скорости ракеты-носителя добавляется от 0 (на полюсах) до 0,4651 км/с (на экваторе) скорости вращения Земли, а при старте в западном направлении (на ретроградную орбиту) скорость ракеты при старте уменьшается на ту же величину, что приводит к уменьшению полезной нагрузки ракеты-носителя (как у израильской ракеты «Шавит»).
Орбитальные процедуры
| Манёвр | Требуемая Δv за год [м/с] | ||
|---|---|---|---|
| Средняя | Макс. | ||
| Компенсация сопротивления атмосферы на высоте орбиты… | 400—500 км | < 25 | < 100 |
| 500—600 км | < 5 | < 25 | |
| > 600 км | < 7.5 | ||
| Контроль положения аппарата (по трём осям) на орбите | 2—6 | ||
| Удержание аппарата в орбитальной позиции на ГСО | 50—55 | ||
| Удержание аппарата в точках Лагранжа L1/L2 | 30—100 | ||
| Удержание аппарата на окололунной орбите[2] | 0—400 | ||
Космические перелёты
Все скорости в таблице ниже указаны в км/с. Диапазоны скоростей указаны, так как Δv вывода на орбиту зависит от места запуска на поверхности Земли и параметров переходных орбит.
| Δv [км/с] от (ниже) и к: | НОО (наклонение 28°) | НОО (экваториальная) | ГСО | Точка Лагранжа L1 | Точка Лагранжа L2 | Точки Лагранжа L4 и L5 | Орбита Луны | Поверхность Луны | Вторая космическая скорость |
|---|---|---|---|---|---|---|---|---|---|
| Поверхность Земли | 9,3—10,0 | 9,3—10,0 | 13,2—18,2 | 13,9—15,6 | |||||
| НОО Земли, 28° | X | 4,24 | 4,33 | 3,77 | 3,43 | 3,97 | 4,04 | 5,93 | 3,22 |
| НОО Земли, экватор | 4,24 | X | 3,90 | 3,77 | 3,43 | 3,99 | 4,04 | 5,93 | 3,22 |
| ГСО | 2,06 | 1,63 | X | 1,38 | 1,47 | 1,71 | 2,05 | 3,92 | 1,30 |
| Точка Лагранжа L1 | 0,77 | 0,77 | 1,38 | X | 0,14 | 0,33 | 0,64 | 2,52 | 0,14 |
| Точка Лагранжа L2 | 0,33 | 0,33 | 1,47 | 0,14 | X | 0,34 | 0,64 | 2,52 | 0,14 |
| Точки Лагранжа L4 и L5 | 0,84 | 0,98 | 1,71 | 0,33 | 0,34 | X | 0,98 | 2,58 | 0,43 |
| Низкая орбита Луны (LLO) | 1,31 | 1,31 | 2,05 | 0,64 | 0,65 | 0,98 | X | 1,87 | 1,40 |
| Поверхность Луны | 2,74 | 2,74 | 3,92 | 2,52 | 2,53 | 2,58 | 1,87 | X | 2,80 |
| Вторая космическая скорость для Земли | 2,9 | 1,30 | 0,14 | 0,14 | 0,43 | 1,40 | 2,80 | X |
Примечания
- ↑ Архивированная копия. Дата обращения: 5 марта 2017. Архивировано из оригинала 6 марта 2017 года. Архивная копия от 6 марта 2017 на Wayback Machine
- ↑ Frozen lunar orbits Архивировано 9 февраля 2007 года.
- ↑ list of delta-v (недоступная ссылка)
- ↑ L2 Halo lunar orbit. Дата обращения: 28 января 2015. Архивировано из оригинала 25 декабря 2015 года. Архивная копия от 25 декабря 2015 на Wayback Machine
- ↑ Strategic Considerations for Cislunar Space Infrastructure. Дата обращения: 28 января 2015. Архивировано из оригинала 22 февраля 2013 года. Архивная копия от 22 февраля 2013 на Wayback Machine
Литература
- Мещерский И. В. Работы по механике тел переменной массы. — М.—Л.: ГИТТЛ, 1949. (2-е изд. 1952.)
- Космодемьянский А. А. Механика тел переменной массы (Теория реактивного движения). Ч. 1. — М., 1947.
- Михайлов Г. К. К истории динамики систем переменного состава // Известия АН СССР: Механика твердого тела. — 1975. — № 5. — С. 41—51.
- Гурин А. И. Основы механики тел переменной массы и ракетодинамике. — М., 1960. — 222 с.
- Мандрыка А. П. Генезис современной ракетодинамики. — Л.: Наука, 1971. — 216 с.
Ссылки
- Журнал «Астронавтика и ракетодинамика» ВИНИТИ (недоступная ссылка)