Цена стабильности

Цена стабильности (англ. price of stability, PoS) для игры — отношение оптимального значения целевой функции в одном из её равновесных состояний и оптимального исхода. Цена стабильности имеет смысл для игр, которые имеют некую высшую силу или условия игры, которые каким-либо образом влияют на положение игроков и могут помочь им сойтись к равновесию Нэша. При измерении эффективности равновесия Нэша в какой-либо игре имеет смысл рассматривать и цену анархии (англ. Price of Anarchy, PoA).

PoS можно выразить следующим образом:

${\displaystyle PoS={\frac {N}{S}},\ PoS\geqslant 0.}$

Здесь ${\textstyle N}$ — значение лучшего равновесия Нэша, ${\textstyle S}$ — значение оптимального решения.

В приведённой ниже игре «Дилемма заключённого» игроки не всегда будут сотрудничать друг с другом, даже если это в их интересах, поскольку имеется единственное равновесие (${\textstyle B}$, ${\textstyle R}$), мы имеем ${\displaystyle PoS=PoA={\tfrac {1}{2}}}$.

Дилемма заключённого

	${\textstyle L}$	${\textstyle R}$
${\textstyle T}$	(2,2)	(0,3)
${\textstyle B}$	(3,0)	(1,1)

Этот пример является версией игры «битва полов». В нем имеются две точки равновесия, (${\textstyle T}$, ${\textstyle L}$) и (${\textstyle B}$, ${\textstyle R}$) со значениями 3 и 15 соответственно. Оптимальным значением является 15. Тогда ${\displaystyle PoS=1}$, в то время как ${\displaystyle PoA={\tfrac {1}{5}}}$.

Битва полов

	${\textstyle L}$	${\textstyle R}$
${\textstyle T}$	(2,1)	(0,0)
${\textstyle B}$	(0,0)	(5,10)

Цену стабильности первыми изучили А. Шульцан и Н. Мозес, а сам термин появился в работах Е. Аншелевича. Они показали, что равновесие Нэша всегда существует в чистых стратегиях, и цена стабильности этой игры не превосходит n-го гармонического числа в ориентированных графах. Для неориентированных графов Аншелевич и другие представили определили жёсткую границу стабильности в 4/3 для случая одного источника и двух игроков. Йен Ли доказал, что для таких графов с различными точками назначения для всех игроков, с которыми все игроки должны иметь связь, цена стабильности потока игры на построение сети Шепли равна ${\displaystyle O(\log n/\log \log n),}$ где ${\displaystyle n}$ — число игроков. С другой стороны, цена анархии для игры равна примерно ${\displaystyle n}$.

Игры построения сети имеют естественное обоснование для цены стабильности. В этих играх цена анархии может быть намного меньше цены стабильности.

Пример следующей игры:

• ${\displaystyle n}$ игроков;
• целью каждого ${\displaystyle i}$-го игрока является соединение вершин ${\displaystyle s_{i}}$ и ${\displaystyle t_{i}}$ в ориентированном графе ${\displaystyle G=(V,E)}$;
• стратегиями ${\displaystyle P_{i}}$ для игрока являются все пути из ${\displaystyle s_{i}}$ в ${\displaystyle t_{i}}$ в графе ${\displaystyle G}$;
• каждая дуга имеет цену ${\displaystyle c_{i}}$;
• «справедливое распределение цен»: Если ${\displaystyle n_{e}}$ игроков выбирают дугу ${\displaystyle e}$, то цена ${\displaystyle d_{e}(n_{e})={\frac {c_{e}}{n_{e}}}}$ распределяется равно между ними;
• цена для игрока составляет ${\displaystyle C_{i}(S)=\sum _{e\in P_{i}}{\frac {c_{e}}{n_{e}}}}$;
• социальная цена равна сумме цен для игроков: ${\displaystyle SC(S)=\sum _{i}C_{i}(S)=\sum _{e\in S}n_{e}{\frac {c_{e}}{n_{e}}}=\sum _{e\in S}c_{e}}$.

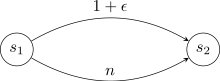
Цена анархии может составлять ${\displaystyle \Omega (n)}$. Пример следующей игры на построение сети.

В этой игре есть 2 различных равновесия. Если все разделяют дугу ${\displaystyle 1+\varepsilon }$, то социальная цена равна ${\displaystyle 1+\varepsilon }$. Более того, это равновесие оптимально. Однако, разделение всеми дуги ${\displaystyle n}$ является также равновесием Нэша. Любой агент имеет цену ${\displaystyle 1}$ в равновесной стратегии, и переключение его на другую дугу повышает его цену до ${\displaystyle 1+\varepsilon }$.

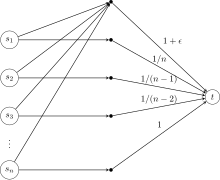
Здесь приведена патологическая игра с таким же поведением, но уже для цены стабильности. Присутствует ${\displaystyle n}$ игроков, каждый из которых начинает с вершины ${\displaystyle s_{i}}$ и пытается соединить её с вершиной ${\displaystyle t}$. Допустим, цены непомеченных дуг равны 0.

Оптимальной стратегией для всех игроков является общее использование дуги ${\displaystyle 1+\varepsilon }$, что даёт социальную цену ${\displaystyle 1+\varepsilon }$. Однако имеется единственная стратегия с равновесием Нэша для этой игры. В случае оптимальности, каждый игрок платит ${\displaystyle \textstyle {\frac {1+\varepsilon }{n}}}$ и игрок 1 может уменьшить свою цену путём переключения на дугу ${\displaystyle {\tfrac {1}{n}}}$. Если это происходит, то игроку 2 становится выгодным переключиться на дугу ${\displaystyle {\tfrac {1}{n-1}}}$ и так далее. В конце концов, агенты достигнут равновесия Нэша, оплачивая свою собственную отдельную дугу. Такое распределение имеет социальную цену ${\displaystyle 1+{\tfrac {1}{2}}+\cdots +{\tfrac {1}{n}}=H_{n}}$, где ${\displaystyle H_{n}}$ является ${\displaystyle n}$-ым гармоническим числом, что равно ${\displaystyle \Theta (\log n)}$. Хотя это значение не ограничено, цена стабильности экспоненциально лучше цены анархии в этой игре.

По определению игры на построение сети являются играми на переполнение^[англ.], поэтому они допускают потенциальную функцию ${\displaystyle \Phi =\sum _{e}\sum _{i=1}^{n_{e}}{\frac {c_{e}}{i}}}$.

Теорема. [Теорема 19.13 из книги 1] Предположим, что существует константы ${\displaystyle A}$ и ${\displaystyle B}$, такие, что для любой стратегии ${\displaystyle S}$

${\displaystyle A\cdot SC(S)\leqslant \Phi (S)\leqslant B\cdot SC(S).}$

Тогда цена стабильности меньше ${\displaystyle B/A}$.

Доказательство. Глобальный минимум ${\displaystyle NE}$ функции ${\displaystyle \Phi }$ является равновесием Нэша, так что

${\displaystyle SC(NE)\leqslant 1/A\cdot \Phi (NE)\leqslant 1/A\cdot \Phi (OPT)\leqslant B/A\cdot SC(OPT).}$

Социальная цена была определена как сумма цен по дугам, так что

${\displaystyle \Phi (S)=\sum _{e\in S}\sum _{i=1}^{n_{e}}{\frac {c_{e}}{i}}=\sum _{e\in S}c_{e}H_{n_{e}}\leqslant \sum _{e\in S}c_{e}H_{n}=H_{n}\cdot SC(S).}$

Тривиально получаем ${\displaystyle A=1}$ и вычисления выше дают ${\displaystyle B=H_{n}}$, так что можно привлечь теорему для верхней границы цены стабильности.

• Распределение объектов (конкурентная игра)^[англ.] — игра без цены стабильности.