Центробежная сила

Центробе́жная си́ла в механике — многозначное понятие, сложившееся как исторически, так и в связи с неупорядоченностью научно-технической терминологии и разногласиями в научной-технической среде.

Центробежные силы относятся к криволинейному движению тела или материальной точки и, согласно Большой советской энциклопедии и ряду других энциклопедических источников, определяются следующим образом:

Центробежная сила — сила, с которой движущаяся материальная точка действует на тело (связь), стесняющее свободу движения точки и вынуждающее её двигаться криволинейно. Численно Ц. с. равна ${\displaystyle mv^{2}/r}$, где ${\displaystyle m}$ — масса точки, ${\displaystyle v}$, — её скорость, ${\displaystyle r}$ — радиус кривизны траектории, и направлена по главной нормали к траектории от центра кривизны (от центра окружности при движении точки по окружности). Ц. с. и центростремительная сила численно равны друг другу и направлены вдоль одной прямой в противоположные стороны, но приложены к разным телам, как силы действия и противодействия. Например, при вращении в горизонтальной плоскости привязанного к верёвке груза центростремительная сила действует со стороны верёвки на груз, вынуждая его двигаться по окружности, а Ц. с. действует со стороны груза на верёвку, натягивает её.

При применении к решению задач динамики д’Аламбера термину Ц. с. придают иногда другой смысл и называют Ц. с. составляющую силы инерции материальной точки, направленную по главной нормали к траектории.

Изредка Ц. с. называют также нормальную составляющую переносной силы инерции при составлении уравнений относительного движения

— Центробежная сила (БСЭ), 1978

По существу в этом определении под словосочетанием центробежная сила имеются в виду три различных значения этого термина. Рассмотрим их подробнее.

1) Центробежная сила в первом значении — ньютонова центробежная сила. На рисунке изображены: диск, равномерно вращающийся вокруг вертикальной оси, верёвка, один конец которой соединён с центром диска, а к другому концу привязан шарик. (Система отсчёта инерциальная, связанная с поверхностью Земли).

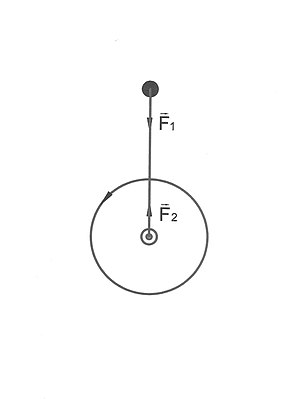
На шарик действует сила натяжения верёвки ${\displaystyle {\vec {F}}_{1}}$, направленная к центру вращения, которая искривляет траекторию движения шарика и заставляет его двигаться по окружности. Эта сила называется центростремительной. Центробежная сила также создается натяжением верёвки, но она приложена к другому телу — диску. Таким образом, центробежная и центростремительная силы в первом значении приложены к разным телам. (Верёвка в данном примере полагается нерастяжимой).

Центростремительная и центробежная силы в данном контексте выступают как обычные силы действия и противодействия по третьему закону Ньютона. Своим названием они обязаны исключительно направлению, по которому они действуют (к центру или от центра) и никакой другой смысловой нагрузки не несут. Некоторые авторы, следуя академику Ишлинскому, называют эти силы ньютоновыми или «настоящими» силами.

2) Центробежная сила во втором её значении называется д’аламберова центробежная сила.

Д’Аламберова центробежная сила является частным случаем д’аламберовой силы инерции, которая мысленно вводится в расчётную схему сил для получения формальной возможности записи уравнений динамики в виде более простых уравнений статики. Она не существует в действительности, не может быть ни ощутима, ни измерена, и относится к категории фиктивных, ненастоящих или псевдосил.

3) В третьем значении центробежной силой называется «нормальная составляющая переносной силы инерции при составлении уравнений относительного движения»^[1]. Эта сила представляет собой частный случай инерционных сил, возникающих в неинерциальных системах отсчёта.

Поясним это на примере.

Представим себе диск, равномерно вращающийся вокруг вертикальной оси с угловой скоростью ${\displaystyle \omega }$. На диске в радиальном направлении установлена направляющая, на которую надеты шарик и пружина растяжения. Шарик имеет возможность перемещения вдоль направляющей. Один конец пружины соединён с шариком, а другой зацеплён за ось диска. Относительно вращающегося диска шарик с пружиной находятся в состоянии покоя. При равномерном вращении диска тангенциальные силы и ускорение отсутствуют, а сила растяжения пружины ${\displaystyle {\vec {F}}_{\text{пр}}}$, действующая на шарик в радиальном направлении равна произведению массы шарика ${\displaystyle m}$ на нормальное (центростремительное) ускорение ${\displaystyle {\vec {F}}_{\text{пр}}=m{\vec {a}}_{\text{ц}}}$ или

${\displaystyle {\vec {F}}_{\text{пр}}=m\omega ^{2}{\vec {r}}}$,

где ${\displaystyle {\vec {r}}}$ — радиус-вектор, проведённый из центра шарика к центру диска.

Такую картину увидит наблюдатель, покоящийся в инерционной системе отсчёта, ${\displaystyle K}$, связанной с поверхностью Земли. Если выбрать неинерциальную систему отсчёта ${\displaystyle K'}$, связанную с диском, то, с точки зрения наблюдателя, находящегося в этой системе, диск вместе с шариком покоятся, а равновесие шарика объясняется действием двух сил: силы, стремящейся удалить его от центра диска — центробежной силы инерции ${\displaystyle {\vec {F}}_{\text{ц}}}$ и силы растяжения пружины, ${\displaystyle {\vec {F}}_{\text{пр}}}$, направленной к центру:

${\displaystyle {\vec {F}}_{\text{пр}}+{\vec {F}}_{\text{ц}}=0}$ или ${\displaystyle {\vec {F}}_{\text{ц}}=-{\vec {F}}_{\text{пр}}}$

По терминологии, предложенной академиком А. Ю. Ишлинским, центробежные силы инерции, иногда называют эйлеровыми силами. (Как известно, Л. Эйлер впервые использовал подвижные системы координат для решения сложных задач механики). ^[2] Примерами этих центробежных сил инерции являются силы, действующие на пассажиров транспорта на крутых поворотах, на лётчиков, совершающих виражи и фигуры высшего пилотажа, и на участников различных цирковых и парковых аттракционов (американские горки, центрифуга, карусели и т. п.). В отличие от фиктивных д’аламберовых сил, эйлеровы центробежные силы инерции имеют признаки, сближающие их с реальными силами. Эти силы можно ощутить и измерить. Вопрос о признании эйлеровых сил «настоящими» силами до сих пор остаётся дискуссионным.

Fц =m(V^2)/r = m(w^2)r = m(V/r)wr = mVw = Pw,

где P - импульс массивного тела m, движущегося со скорость V,

w - угловая скорость изменения в пространстве направления вектора импульса движущегося массивного тела m.

Центробежная сила возникает при изменении направления в пространстве вектора импульса Р, движущегося массивного тела m, со скоростью V, при воздействии на тело m внешней силы, выводящей его из состояния равномерного и прямолинейного движения. Или, при воздействии на это тело m, связи, вынуждающей его двигаться по криволинейной траектории. Центробежная сила, является реальной физической силой, обусловленной свойством инертности массы.

Историческая справка

Понятия силы инерции и центробежная сила впервые упоминаются у Ньютона в его классической книге «Математические начала натуральной философии». Говоря о «врождённой силе материи», то есть о свойстве любого тела сохранять своё состояние покоя или равномерного прямолинейного движения в отсутствии действия каких-либо сил, Ньютон не даёт чёткого определения силы инерции и смешивает понятие инерция — состояние, в котором находится тело, с понятием инертность — свойство тела. Ньютон также использует термин центробежная сила, но рассматривает её как реальную физическую силу, то есть в первом значении, согласно БСЭ. Подобное смешение терминов сохраняется и по сей день.^[3]

В 1743 г. д’Аламбер предложил другой подход к силам инерции, в частности, к центробежной силе инерции. Он сформулировал фундаментальный принцип д’Аламбера, суть которого состоит в том, что, для упрощения решения динамической задачи в инерциальной системе отсчёта, к реально действующим силам ${\displaystyle {\vec {F}}_{i}}$ искусственно добавлялись фиктивные силы инерции, равные им по величине, но противоположно направленные ${\displaystyle {\vec {F}}_{u}=-m{\vec {a}}}$, где ${\displaystyle {\vec {a}}}$ — ускорение тела. В результате уравнение движения тела принимает вид ${\displaystyle \sum ({\vec {F}}_{i}+{\vec {F}}_{u})=0}$, и сводится к решению задачи статической.^[3]

Пожалуй, ни одно из положений теоретической механики не вызывало столько споров и путаницы, как принцип д’Аламбера. В 20-е годы прошлого века против него выступили философы, обвинявшие автора в недиалектичности, поскольку изучение движения по д’Аламберу сводится к изучению статической задачи — равновесия, которое является частным случаем задачи динамической. ^[4]

В 1936—1937 годах в советской прессе возникла дискуссия о силах инерции, в частности, о центробежной силе, между инженерами-практиками и механиками-теоретиками по вопросу критики взглядов на инерцию известного советского учёного — механика Л. Б. Левенсона, который писал о том, что практики давно уже ведут расчёты машин, учитывая реальность сил инерции, а теоретики, не считаясь с фактами, настаивают на нереальности сил инерции и утверждают, что эти силы вовсе не существуют. В 1940 г. вышла книга профессора С. Э. Хайкина «Что такое силы инерции», в которой он выступал с позиций учёных — сторонников реальности инерционных сил. ^[5]

Известны несколько ожесточённых дискуссий в среде специалистов по механике по поводу того, следует ли считать силы инерции реальными силами или же относить их к воображаемым или фиктивным. Последняя такая дискуссия прошла в Институте проблем механики АН СССР между сторонниками академика А. Ю. Ишлинского (считал, что силы инерции фиктивны) и сторонниками академика Л. И. Седова (считал, что силы инерции реальны) на Всесоюзном совещании «Основы классической механики и их роль в преподавании механики» (Москва, 1-8 октября 1985 г). Выдающиеся учёные разругались и разошлись, не решив окончательно проблемы.

Многочисленные дискуссии по поводу центробежных сил носят, по существу, терминологический характер, так как всё зависит от способа определения понятия сила и оттого, что, именно, понимается под термином центробежная сила. Рассмотрим мнения и доводы обеих сторон. Сторонники Ишлинского «настоящей» центробежной силой называют силу противодействия, которая в инерционной системе отсчёта, согласно третьему закону механики, приложена к связи. д’Аламберовы и эйлеровы центробежные силы считаются ненастоящими, фиктивными, поскольку д’аламберовы силы не подчиняются второму и третьему законам Ньютона, а эйлеровы (инерционные) центробежные силы не подчиняются третьему закону Ньютона.

Например, в курсе физики Фриш и Тиморевой т. I § 21 утверждается: «центростремительная и центробежная силы — это те две силы, существование которых обусловлено третьим законом Ньютона; приложены они к разным телам. Например, в случае вращения камня, привязанного к верёвке, центростремительная сила приложена к камню, а центробежная — к верёвке».^[6] К этому следует добавить, что речь идёт об инерциальной системе отсчёта. Аналогичное определение центростремительной и центробежной сил даётся и в школьном курсе физики Пёрышкина.^[7]

В следующем параграфе (§ 22) курса физики Фриш и Тиморевой говорится уже об инерционной центробежной силе, действующей во вращательной системе, которую, по мнению авторов, «иногда называют инерциальной центробежной силой. Её не следует смешивать с той действительной центробежной силой, о которой шла речь в § 21».^[8]

Против названий центростремительная и центробежная для «ньютоновых» сил взаимодействия, при вращательном движении в инерциальной системе отсчёта, у противников Ишлинского есть ряд возражений. По мнению Хайкина эти названия, строго говоря, не нужны. Вполне достаточно знать, что сила, приложенная к вращающему телу со стороны верёвки, есть действующая, а сила, приложенная к верёвке со стороны тела — противодействующая. Названия сил центростремительная и центробежная никакой смысловой нагрузки, кроме указания направления их действия не несут, зато создают ложное впечатление о существовании каких-то новых специфических сил, относящихся исключительно к вращательному движению, что является вредным заблуждением: центробежные и центростремительные силы в инерциальной системе это обычные силы взаимодействия.^[9]

Кстати, во многих учебниках и учебных пособиях силу, создающую центростремительное ускорение в инерциальной системе называют центростремительной, но противодействующую ей силу, действующую на связь, называют силой реакции, либо, вообще, никак не называют за ненадобностью.^[10], ^{[11] [12]}

Однако, главной точкой противостояния сторонников Ишлинского и сторонников Седова является вопрос реальности или фиктивности эйлеровых центробежных сил инерции. Если по вопросу фиктивности д’аламберовых сил инерции нет особых разногласий, то вопрос о реальности эйлеровых сил инерции находится в центре дискуссии. Использование эйлеровых сил инерции, в частности, центробежной силы инерции, позволяет применять второй закон Ньютона в неинерциальных системах отсчёта. Но, в отличие от д’аламберовых сил, вводимых искусственно, эйлеровы центробежные силы инерции возникают при переходе из инерциальной системы отсчёта в неинерциальную и исчезают при обратном переходе. Эти силы имеют признаки, сближающие их с настоящими силами, поскольку их можно ощутить и измерить, а в определённых случаях невозможно отличить от настоящих сил. Единственным серьёзным доводом не считать центробежные силы инерции силами настоящими является тот факт, что источник их происхождения неизвестен из-за отсутствия взаимодействующего тела. Поэтому они не подчиняются третьему закону Ньютона — равенства сил действия и противодействия.

По мнению Д. В. Сивухина: движение тел под действием сил инерции аналогично движению во внешних силовых полях. Силы инерции всегда являются внешними по отношению к любой движущейся системе материальных тел. Что касается реальности или фиктивности сил инерции, то ответ на этот вопрос зависит от смысла, который вкладывается в слова реальный и фиктивный. Если придерживаться ньютоновской механики, согласно которой все силы должны быть результатом взаимодействия тел, то на силы инерции следует смотреть как на фиктивные силы, исчезающие в инерциальных системах отсчёта. Однако, такая точка зрения необязательна. Все взаимодействия осуществляются посредством силовых полей и передаются с конечными скоростями. И на силы инерции можно смотреть как на действия, которым подвергаются тела со стороны каких-то реальных силовых полей.^[13] Аналогичное мнение высказал Г. В. Егоров: «Многочисленные дискуссии по поводу реальности сил инерции носят, по существу, терминологический характер, так как всё зависит от способа определения понятия сила. Если, как это обычно делается, определять силу как физическую величину, являющуюся мерой количественного действия других тел или полей на данное тело, то сила инерции является воображаемой силой, потому что мы не можем указать её источник — тело, со стороны которого она действует. Однако, если силу трактовать как причину ускорения тела, то сила инерции ничем не хуже других сил. Неприменимость третьего закона Ньютона в этом случае принципиального значения не имеет, так как для любой физической системы силы инерции всегда будут внешними силами, а третий закон Ньютона существенен только для внутренних сил, действующих между телами, входящими в систему. Для любого из тел, находящихся в неинерциальной системе отсчёта, силы инерции являются внешними; следовательно, здесь нет замкнутых систем.».^[3].

Отсутствие единой общепризнанной терминологии в учебниках и научной литературе по физике и механике, касающейся центробежных сил инерции, приводит к путанице понятий, ошибкам, парадоксам, а иногда и к полному непониманию сути изучаемого вопроса. Один из примеров такого рода описан в Общем курсе физики Д. В. Сивухина. Автор пишет:

«Центробежные силы, как и всякие силы инерции, существуют лишь в ускоренно движущихся (вращающихся) системах отсчёта и исчезают при переходе к инерциальным системам. Забыв это, можно прийти к парадоксам, которые часто ставят в тупик школьников. Вот один из самых распространённых парадоксов такого типа. Пусть тело движется по окружности. На него действуют две силы: центростремительная ${\displaystyle {\vec {F}}_{1}}$, направленная к центру окружности, и центробежная ${\displaystyle {\vec {F}}_{2}}$, направленная в противоположную сторону. Эти силы равны по модулю и уравновешивают друг друга. ${\displaystyle {\vec {F}}_{1}+{\vec {F}}_{2}=0.}$ По закону инерции тело должно двигаться прямолинейно и равномерно. Противоречие возникло потому, что движение стали относить к неподвижной (инерциальной) системе отсчёта. А в этой системе никаких центробежных сил не существует. Есть только одна центростремительная сила ${\displaystyle {\vec {F}}_{1}}$, которая и сообщает телу ускорение.

Путаница происходит из-за того, что в технической механике термин центробежная сила иногда употребляют в совершенно другом смысле. Центробежной силой называют силу реакции, с которой тело A, вращающееся по окружности, действует на тело B, принуждающее его совершать это вращение. Равную и противоположно направленную силу, с которой тело B действует на вращающееся тело A, называют центростремительной…. Центростремительная и центробежная силы, так понимаемые, всегда приложены к разным телам…».

Однако, понимая центробежную силу в этом смысле, которая в учебнике Фриш и Тиморевой названа «действительной» центробежной силой, и считать, что она удаляет вращающееся тело от центра, совершенно абсурдно, поскольку эта сила к телу не приложена.^[14]

Единственно, в чём можно «упрекнуть» Сивухина, это то, что указанный им парадокс относится лишь к незадачливым школьникам. Такое же «понимание» центробежных и центростремительных сил нередко встречается у студентов, аспирантов, инженеров и даже у преподавателей физики.

Вот пример из широко распространённой в США книги Л. Эллиот и У. Уилкокса «Физика», которая вышла в переводе на русский язык под ред. А. И. Китайгородского в 1975 году. В главе 17 этой книги рассматривается простейший случай равномерного движения по окружности шарика, привязанного к верёвке. К шарику приложены четыре силы: ${\displaystyle {\vec {F}}_{1}}$ — движущая сила, направленная по касательной к окружности и, равная ей по величине, но противоположно направленная, сила инерции ${\displaystyle {\vec {F}}_{2},}$ а также сила ${\displaystyle {\vec {F}}_{4}}$, направленная к центру окружности и, равная ей по величине, сила ${\displaystyle {\vec {F}}_{3}}$, направленная в противоположную сторону (от центра). Далее, по тексту: «Сила ${\displaystyle {\vec {F}}_{4}}$, тянущая тело к центру и сворачивающая тело с прямолинейного пути, называется центростремительной силой. Но центростремительная сила — это не единственная сила, действующая во время движения по окружности, потому что, согласно третьему закону Ньютона, силы всегда действуют парами. Если существует центростремительная сила, то должна быть и другая сила ${\displaystyle {\vec {F}}_{3}}$, равная ей по величине, но противоположная по направлению. Эта сила называется центробежной силой…» ^[15] Казалось бы, исходя из написанного, речь идёт об инерциальной системе и центробежной силе в её первом значении, согласно БСЭ. Но, в следующем абзаце читаем: «Действие центробежной силы ощущают на себе пассажиры, едущие в автобусе или автомобиле, когда машина делает крутой поворот.» Стало быть речь идёт о неинерциальной системе отсчёта и уже о центробежной силе инерции во втором её значении, а это как раз тот же самый, описанный Сивухиным случай путаницы и неразберихи, но уже не в голове школьника, а в учебной литературе. Из всего сказанного можно сделать вывод: пока не будет разработана единая система терминологии, следует внимательно относиться к выражению центробежная сила и в каждом конкретном случае выяснять, к какому понятию оно относится.

• Центробежная сила // Большая Советская Энциклопедия. — Советская Энциклопедия, 1978. — Т. 28. — С. 525.
• Гулиа Н. В. Инерция. — М.: Наука, 1982. — 152 с.
• Егоров Г. В. Силы инерции. — Вестник Брянского государственного университета, 2013. — № 1.
• Ишлинский А. Ю. Классическая механика и силы инерции. — М.: Наука, 1987. — 320 с.
• Ландсберг Г. С. Элементарный учебник физики. — М.: Наука, 1985. — Т. 1. — 606 с.
• Милковская Л. Б. Повторим физику. — М.: Высшая школа, 1972. — 608 с.
• Пёрышкин А. В. Курс физики (часть вторая). — 9-е изд. — М.: Учпедгиз, 1957. — 216 с.
• Савельев И. В. Курс физики. — М.: Наука, 1989. — Т. 1. — 496 с. — ISBN 5-02-014052-x:5-02-014430-4.
• Селезнёв Ю. А. Основы элементарной физики. — 3-е изд. — М.: Наука, 1969. — 496 с.
• Сивухин, Д.В. Общий курс физики. — 4-е изд. — М.: Физматлит; МФТИ, 2005. — Т. 1. — 560 с. — ISBN 5-9221-0225-7;5-89155-078-4.
• Фриш С. Э.,Тиморева А. В. Курс общей физики. — 10-е изд. — М.: Физматлит, 1962. — Т. 1. — 468 с.
• Хайкин, С.Э. Силы инерции и невесомость. — М.: Наука, 1967. — 312 с.
• Эллиот Л., Уилкокс У. Физика. — М., 1975. — 736 с.