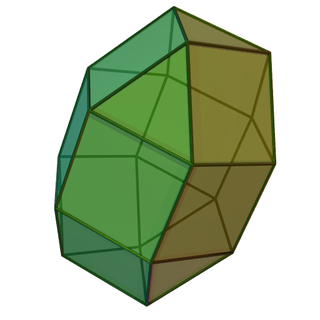
Четырёхскатный купол

Четырёхскатный купол
Четырёхскатный купол
Тип	Многогранник Джонсона J3 - J4 - J5
Свойства	выпуклый
Комбинаторика
Элементы	20 рёбер 12 вершин
Грани	4 треугольников,<1 + 4 квадратов 1 восьмиугольник
Конфигурация вершины	8(3.4.8) 4(3.43)
Развёртка
Классификация
Символ Шлефли	{4}||t{4}
Группа симметрии	C4v, [4], (*44)
Группа вращения	C4, [4]+, (44)

Четырёхска́тный ку́пол — один из многогранников Джонсона (J₄ = (по Залгаллеру) М₅). Его можно получить как срез ромбокубооктаэдра. Как и у всех куполов, многоугольник в основании имеет удвоенное число рёбер и вершин по сравнению с верхним многоугольником. В нашем случае основанием является восьмиугольник.

Многогранник Джонсона — один из 92 строго выпуклых многогранников, имеющих правильные грани, но не являющийся однородным (то есть он не правильный, не архимедов, не призма или антипризма). Название многограннику дал Норман Джонсон, который первым перечислил эти многогранники в 1966 году^[1].

Следующие формулы для объёма, площади поверхности и радиуса описанной сферы могут быть использованы, если все грани являются правильными многоугольниками со сторонами a^[2]:

${\displaystyle V=(1+{\frac {2{\sqrt {2}}}{3}})a^{3}\approx 1.94281...a^{3}}$

${\displaystyle A=(7+2{\sqrt {2}}+{\sqrt {3}})a^{2}\approx 11.5605...a^{2}}$

${\displaystyle C=({\frac {1}{2}}{\sqrt {5+2{\sqrt {2}}}})a\approx 1.39897...a}$

Семейство выпуклых куполов

n	2	3	4	5	6
Название	{2} || t{2}	{3} || t{3}	{4} || t{4}	{5} || t{5}	{6} || t{6}
Купол	Диагональный купол	Трёхскатный купол	Четырёхскатный купол	Пятискатный купол	Шестискатный купол (плоский)
Связанные однородные многогранники	Треугольная призма	Кубооктаэдр	Ромбокубо- октаэдр	Ромбоикосо- додекаэдр	Ромботри- шестиугольная мозаика[англ.]

Двойственный многогранник для четырёхскатного купола имеет 8 треугольных и 4 дельтоидных граней:

Двойственный многогранник для четырёхскатного купола	Развёртка двойственного многогранника

Скрещённый квадратный купол^[англ.] — один из невыпуклых изоморфов многогранника Джонсона, который топологически идентичен выпуклому четырёхскатному куполу. Он может быть получен как срез невыпуклого большого ромбокубооктаэдра^[англ.] или квазиромбокубооктаэдра, что аналогично получению купола как среза ромбокубооктаэдра. Как и у всех куполов, многоугольник в основании имеет удвоенное число рёбер и вершин по сравнению с верхним многоугольником. В нашем случае основанием является октаграмма.

Четырёхскатный купол является компонентой некоторых неоднородных заполняющих пространство рёшёток:

• с тетраэдрами;
• с кубами и кубооктаэдрами
• с тетраэдрами, квадратными пирамидами и различными комбинациями кубов, удлинённых четырёхугольных пирамид и удлинённых четырёхугольных бипирамид^[3].

• Четырёхскатный купол, Многогранник Джонсона (англ.) Вайсстайн, Эрик, MathWorld