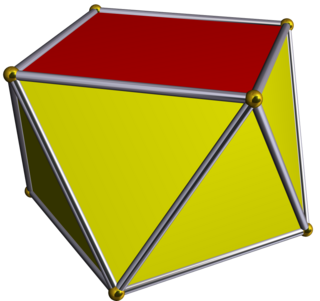
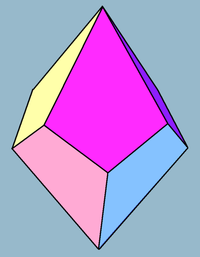
Четырёхугольный трапецоэдр
| Четырёхугольный трапецоэдр | |
|---|---|
 | |
| Тип | трапецоэдр |
| Конвей | dA4 |
| Диаграмма Коксетера | |
| Грани | 8 дельтоидов |
| Рёбер | 16 |
| Вершин | 10 |
| Конфигурация граней | V4.3.3.3 |
| Группа симметрии | D4d, [2+,8], (2*4), order 16 |
| Группа вращений | D4, [2,4]+, (224), order 8 |
| Двойственный многогранник | Квадратная антипризма |
| Свойства | выпуклый, транзитивин по граням |
Четырёхугольный трапецоэдр или дельтоэдр — это второй многогранник в бесконечной серии многогранников с однородными гранями, которые являются двойственными антипризмам. Многогранник имеет восемь граней, которые конгруэнтны дельтоидам. Многогранник двойственен квадратной антипризме.
Использование для генерации сеток
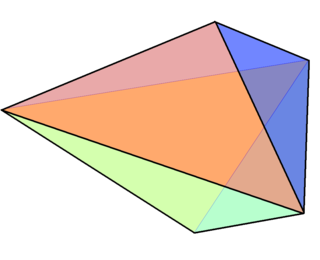
Это тело используется как тестовый случай при генерации шестиугольных расчётных сеток[1][2][3][4][5], что упрощает тестирование по сравнению с тестом Роба Шнайдера в виде квадратной пирамиды с границами, поделёнными на 16 четырёхугольников. В этом контексте четырёхугольный трапецоэдр называют также кубическим октаэдром[3], четырёхугольным октаэдром[4], или восьмиугольным веретеном[5], поскольку тело имеет восемь четырёхугольных граней и однозначно определяется как комбинаторный многогранник этим свойством[3]. Добавление четырёх кубоидов (тел, топологически эквивалентных кубу) в сетку для кубического октаэдра даёт сетку для пирамиды Шнайдера[2]. Будучи простосвязным многогранником (то есть любой путь из рёбер разбивает грани на два несвязных множества) с чётным числом граней, кубический октаэдр может быть разложен на топологические кубоиды с кривыми гранями, которые прилегают друг к друг полными гранями и не нарушают границы четырёхугольников [1][5][6], что позволяет построить явно сетку для этого типа[4]. Однако неясно, можно ли получить такое разложение, в котором все кубоиды будут выпуклыми многогранниками с плоскими гранями[1][5].
Связанные многогранники
| Семейство трапецоэдров V.n.3.3.3 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Многогранники |  |  |  |  |  |  |  |  | ||
| Мозаики |  |  |  |  |  |  |  |  |  | |
| Конфиг. | V2.3.3.3 | V3.3.3.3 | V4.3.3.3 | V5.3.3.3 | V6.3.3.3 | V7.3.3.3 | V8.3.3.3 | ...V10.3.3.3 | ...V12.3.3.3 | ...V∞.3.3.3 |
Четырёхугольный трапецоэдр является первым телом в серии двойственных плосконосых многогранников и мозаик с конфигурацией граней V3.3.4.3.n.
| 4n2 симметрии плосконосых мозаик: 3.3.4.3.n | ||||||||
|---|---|---|---|---|---|---|---|---|
| Симметрия 4n2 | Сферическая | Евклидова | Компактная гиперболическая | Paracomp. | ||||
| 242 | 342 | 442 | 542 | 642 | 742 | 842 | ∞42 | |
| Плосконосые мозаики |  |  |  |  |  |  |  |  |
| Конфиг. | 3.3.4.3.2 | 3.3.4.3.3 | 3.3.4.3.4 | 3.3.4.3.5 | 3.3.4.3.6 | 3.3.4.3.7 | 3.3.4.3.8 | 3.3.4.3.∞ |
| Гиро- мозаики |  |  |  |  | ||||
| Конфиг. | V3.3.4.3.2 | V3.3.4.3.3 | V3.3.4.3.4 | V3.3.4.3.5 | V3.3.4.3.6 | V3.3.4.3.7 | V3.3.4.3.8 | V3.3.4.3.∞ |
Примечания
- ↑ 1 2 3 Eppstein, 1996, с. 58–67.
- ↑ 1 2 Mitchell, 1999, с. 228–235.
- ↑ 1 2 3 Schwartz, Ziegler, 2004, с. 385–413.
- ↑ 1 2 3 Carbonera, Shepherd, 2006, с. 435–452.
- ↑ 1 2 3 4 Erickson, 2013, с. 37–46.
- ↑ Mitchell, 1996, с. 465–476.
Литература
- David Eppstein. Linear complexity hexahedral mesh generation // Proceedings of the Twelfth Annual Symposium on Computational Geometry (SCG '96). — New York, NY, USA: ACM, 1996. — С. 58–67. — doi:10.1145/237218.237237.
- Mitchell S. A. The all-hex geode-template for conforming a diced tetrahedral mesh to any diced hexahedral mesh // Engineering with Computers. — 1999. — Т. 15, вып. 3. — С. 228–235. — doi:10.1007/s003660050018.
- Alexander Schwartz, Günter M. Ziegler. Construction techniques for cubical complexes, odd cubical 4-polytopes, and prescribed dual manifolds // Experimental Mathematics. — 2004. — Т. 13, вып. 4. — С. 385–413.
- Carlos D. Carbonera, Jason F. Shepherd,. A constructive approach to constrained hexahedral mesh generation // Proceedings of the 15th International Meshing Roundtable. — Berlin: Springer, 2006. — С. 435–452. — doi:10.1007/978-3-540-34958-7_25.
- Jeff Erickson. Efficiently hex-meshing things with topology // Proceedings of the Twenty-ninth Annual Symposium on Computational Geometry (SoCG '13). — New York, NY, USA: ACM, 2013. — С. 37–46. — doi:10.1145/2462356.2462403. Архивная копия от 10 августа 2017 на Wayback Machine
- Scott A. Mitchell. A characterization of the quadrilateral meshes of a surface which admit a compatible hexahedral mesh of the enclosed volume // STACS 96: 13th Annual Symposium on Theoretical Aspects of Computer Science Grenoble, France, February 22–24, 1996, Proceedings. — Berlin: Springer, 1996. — Т. 1046. — С. 465–476. — (Lecture Notes in Computer Science). — doi:10.1007/3-540-60922-9_38.
Ссылки
- Paper model tetragonal (square) trapezohedron
- Weisstein, Eric W. Trapezohedron (англ.) на сайте Wolfram MathWorld.