Число́ Рейнольдса , — безразмерная величина, характеризующая отношение инерционных сил к силам вязкого трения в вязких жидкостях и газах.
Ламина́рное тече́ние — течение, при котором жидкость или газ перемещаются слоями без перемешивания и пульсаций.
Те́нзор эне́ргии-и́мпульса (ТЭИ) — симметричный тензор второго ранга (валентности), описывающий плотность и поток энергии и импульса полей материи и определяющий взаимодействие этих полей с гравитационным полем.
Эллиптические функции Якоби — это набор основных эллиптических функций комплексного переменного и вспомогательных тета-функций, которые имеют прямое отношение к некоторым прикладным задачам. Они также имеют полезные аналогии с тригонометрическими функциями, как показывает соответствующее обозначение 
для 
. Они не дают самый простой способ развить общую теорию, как замечено недавно: это может быть сделано на основе эллиптических функций Вейерштрасса. Эллиптические функции Якоби имеют в основном параллелограмме по два простых полюса и два простых нуля.
Альтернативными теориями гравитации принято называть теории гравитации, существующие как альтернативы общей теории относительности (ОТО) или существенно изменяющие её. К альтернативным теориям гравитации часто относят вообще любые теории, не совпадающие с общей теорией относительности хотя бы в деталях или как-то обобщающие её. Тем не менее, нередко теории гравитации, особенно квантовые, совпадающие с общей теорией относительности в низкоэнергетическом пределе, «альтернативными» не называют.
Эллипти́ческий интегра́л — некоторая функция 
над полем действительных или комплексных чисел, которая может быть формально представлена в следующем виде:
,
Модуль сдвига — физическая величина, характеризующая способность материала сопротивляться сдвиговой деформации. Является вторым параметром Ламе. Модуль сдвига определяется следующим соотношением:
Критерий подобия — безразмерная величина, составленная из размерных физических параметров, определяющих рассматриваемое физическое явление. Равенство всех однотипных критериев подобия для двух физических явлений и систем — необходимое и достаточное условие их физического подобия.
Тензор электромагнитного поля — это антисимметричный дважды ковариантный тензор, являющийся обобщением напряжённости электрического и индукции магнитного поля для произвольных преобразований координат. Он используется для инвариантной формулировки уравнений электродинамики, в частности, с его помощью можно легко обобщить электродинамику на случай наличия гравитационного поля.
Число Экмана (Ek) — критерий подобия в гидродинамике, равный отношению внутреннего трения в жидкости к силе Кориолиса. Оно выражается следующим образом:
Число Уомерсли — критерий подобия в гидродинамике, определяющий соотношение между темпом пульсации потока жидкости и её вязкостью. Оно определяется следующим образом:
,
Число Тейлора (Ta) — два сходных критерия подобия в гидродинамике.
Число Лундквиста — критерий подобия в магнитной гидродинамике, равный отношению воздействия альфвеновских волн на жидкость к вязкому трению. Оно определяется следующим образом:
,
Число Ричардсона — критерий подобия в гидродинамике, равный отношению потенциальной энергии тела, погружённого в жидкость к его кинетической энергии. Под «телом» здесь обычно понимается рассматриваемая жидкость или газ.
Нелине́йное, или куби́ческое, уравне́ние Шрёдингера (НУШ) — нелинейное уравнение в частных производных второго порядка, играющее важную роль в теории нелинейных волн, в частности, в нелинейной оптике и физике плазмы.
Функции Кельвина — группа бесселевых функций. Каждая их пара представляют решения дифференциального уравнения:
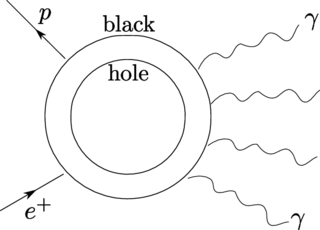
Виртуальная чёрная дыра — гипотетический объект квантовой гравитации: чёрная дыра, возникшая в результате квантовой флуктуации пространства-времени. Является одним из примеров так называемой квантовой пены и гравитационным аналогом виртуальных электрон-позитронных пар в квантовой электродинамике.
Течение Хеле-Шоу определяется как течение жидкости или газа, происходящее между двумя параллельными плоскими пластинами, разделёнными узким зазором, удовлетворяющим определенным условиям. Оно названо в честь Генри Селби Хеле-Шоу, который изучал эту задачу в 1898 году. Различные проблемы механики жидкости можно аппроксимировать течениями Хеле-Шоу, поэтому исследование этих течений имеет важное значение. Аппроксимирование течением Хеле-Шоу особенно важно для микропотоков. Это связано с технологией производства, которая создает неглубокие плоские конфигурации, и обычно низкими числами Рейнольдса микропотоков.
