Кинема́тика точки — раздел кинематики, изучающий математическое описание движения материальных точек. Основной задачей кинематики является описание движения при помощи математического аппарата без выяснения причин, вызывающих это движение.

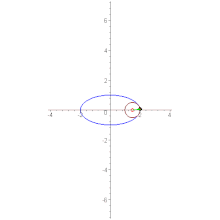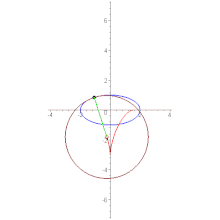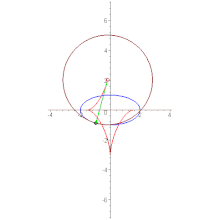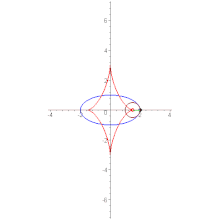
Э́ллипс — замкнутая плоская кривая, исторически определённая как одно из конических сечений . Название эллипсу дал Аполлоний Пергский в своей «Конике».
Дифференциа́льная геоме́трия кривы́х — раздел дифференциальной геометрии, который занимается исследованием гладких пространственных и плоских кривых в евклидовом пространстве аналитическими методами.
Эпицикло́ида — плоская кривая, образуемая фиксированной точкой окружности, катящейся по внешней стороне другой окружности без скольжения.

Цикло́ида — плоская трансцендентная кривая.
Кривизна́ — собирательное название ряда характеристик, описывающих отклонение того или иного геометрического «объекта» от соответствующих «плоских» объектов.

Пряма́я — одно из фундаментальных понятий евклидовой геометрии. При систематическом изложении геометрии прямые линии обычно принимаются за одно из исходных (неопределяемых) понятий, их свойства и связь с другими понятиями определяются аксиомами геометрии.

Пове́рхность в геометрии и топологии — двумерное топологическое многообразие. Наиболее известными примерами поверхностей являются границы геометрических тел в обычном трёхмерном евклидовом пространстве. С другой стороны, существуют поверхности, которые нельзя вложить в трёхмерное евклидово пространство без привлечения сингулярности или самопересечения.

Поде́ра кривой относительно точки — некоторая кривая, составленная из оснований перпендикуляров, опущенных из данной точки на касательные к данной кривой.
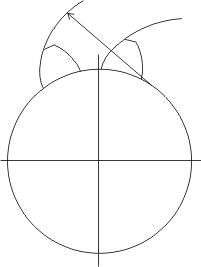
.

Эвольвентой окружности является траектория любой точки прямой линии, перекатываемой по окружности без скольжения. По эвольвенте обрабатывают профиль зубьев зубчатых колёс. Эвольвенту окружности можно получить, сматывая натянутую нить с цилиндрической поверхности. Конец этой нити будет описывать эвольвенту.
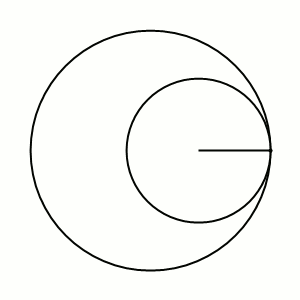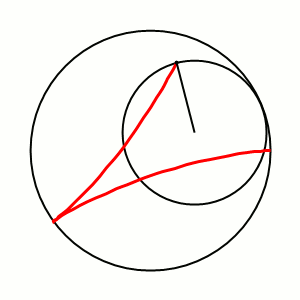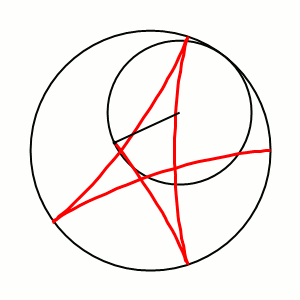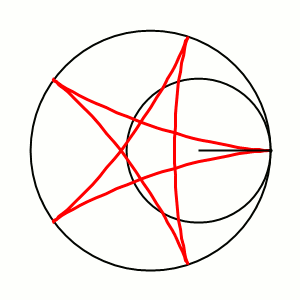
Гипоцикло́ида — плоская кривая, образуемая точкой окружности, катящейся по внутренней стороне другой окружности без скольжения.
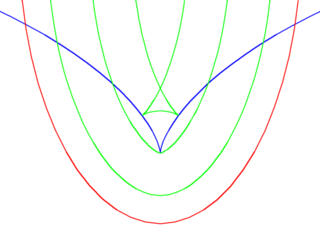
Параллельная кривая или эквидистанта плоской кривой — огибающая семейства окружностей равного радиуса, центры которых лежат на заданной кривой. Понятие параллельной кривой — обобщение понятия параллельной прямой на случай плоских кривых.
Волновое уравнение в физике — линейное гиперболическое дифференциальное уравнение в частных производных, задающее малые поперечные колебания тонкой мембраны или струны, а также другие колебательные процессы в сплошных средах и электромагнетизме (электродинамике). Находит применение и в других областях теоретической физики, например при описании гравитационных волн. Является одним из основных уравнений математической физики.
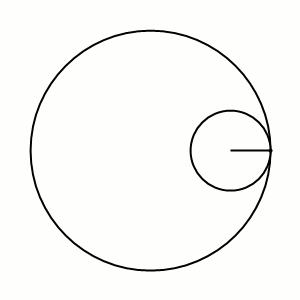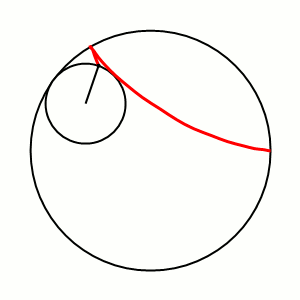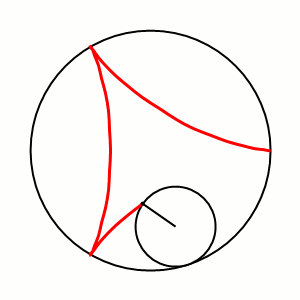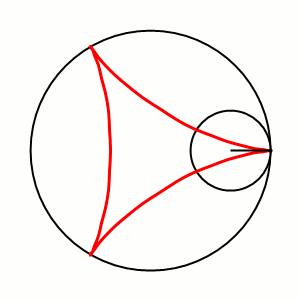
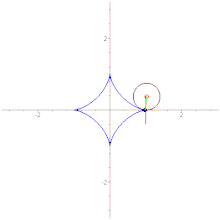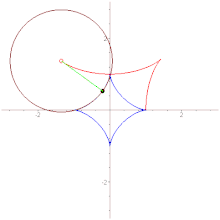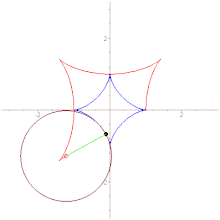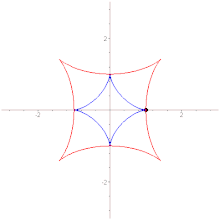
Дельтоида — плоская алгебраическая кривая, описываемая фиксированной точкой окружности, катящейся по внутренней стороне другой окружности, радиус которой втрое больше радиуса первой.

Суперэллипс — геометрическая кривая, задаваемая в декартовых координатах уравнением


Инверсия кривой — результат применения операции инверсии к заданной кривой C. По отношению к фиксированной окружности с центром O и радиусом k инверсия точки Q — это точка P, лежащая на луче OQ, и OP•OQ = k2. Инверсия кривой C — это множество всех точек P, являющихся инверсиями точек Q, принадлежащих кривой C. Точка O в этом построении называется центром инверсии, окружность называется окружностью инверсии, а k — радиусом инверсии.

Элеме́нт длины́ — понятие математического анализа и дифференциальной геометрии, точнее — интегрального исчисления, элемент интегрирования, главная линейная часть приращения длины кривой, то есть малый отрезок касательной к кривой в рассматриваемой точке. Синонимы: дифференциал длины дуги, дифференциал дуги, элемент дуги, линейный элемент.