
Практическое построение окружности возможно с помощью циркуля. Окру́жность — замкнутая плоская кривая, все точки которой равноудалены от заданной точки, лежащей в той же плоскости, что и кривая: эта точка называется центром окружности. Отрезок, соединяющий центр с какой-либо точкой окружности, называется радиусом; радиусом называется также и длина этого отрезка. Окружность разбивает плоскость на две части — конечную внутреннюю и бесконечную внешнюю. Внутренность окружности называется кругом; граничные точки, в зависимости от подхода, круг может включать или не включать.
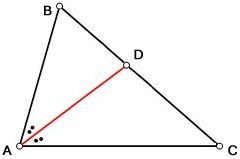
Биссектри́са угла — луч, исходящий из вершины угла и делящий этот угол на два равных угла. Можно также определить биссектрису как геометрическое место точек внутри угла, равноудалённых от сторон этого угла.

Вневпи́санная окружность треугольника — окружность, касающаяся одной из сторон треугольника и продолжений двух других его сторон. У любого треугольника существует три вневписанных окружности.

Окружность называют вписанной в угол, если она лежит внутри угла и касается его сторон. Центр окружности, вписанной в угол, лежит на биссектрисе этого угла.

Серединный треугольник — треугольник, построенный на серединах сторон данного треугольника, частный случай серединного многоугольника.

Описанная окру́жность многоугольника — окружность, содержащая все вершины многоугольника. Центром является точка пересечения серединных перпендикуляров к сторонам многоугольника.

Точка Нагеля — точка пересечения отрезков, соединяющих вершины треугольника с точками касания противоположных сторон с соответствующими вневписанными окружностями.

Центр вписанной окружности треугольника (инцентр) — одна из замечательных точек треугольника, точка пересечения биссектрис треугольника. Центр вписанной в треугольник окружности также иногда называют инцентром.

Прямая Симсона — прямая, проходящая через основания перпендикуляров на стороны треугольника из точки на его описанной окружности. Её существование опирается на теорему Симсона.

Треуго́льник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Указанные три точки называются вершинами треугольника, а отрезки — сторонами треугольника. Часть плоскости, ограниченная сторонами, называется внутренностью треугольника: нередко треугольник рассматривается вместе со своей внутренностью.

Изогона́льное сопряже́ние — геометрическое преобразование, получаемое отражением прямых, соединяющих исходные точки с вершинами заданного треугольника относительно биссектрис углов треугольника.

Формула Эйлера — теорема планиметрии, связывает расстояние между центрами вписанной и описанной окружностей и их радиусами.

Вписанная в треугольник окружность — окружность внутри треугольника, касающаяся всех его сторон; наибольшая окружность, которая может находиться внутри треугольника. Центр этой окружности является точкой пересечения биссектрис треугольника и называется инцентром треугольника.

В евклидовой геометрии описанный четырёхугольник — это выпуклый четырёхугольник, стороны которого являются касательными к одной окружности внутри четырёхугольника. Эта окружность называется вписанной в четырёхугольник. Описанные четырёхугольники являются частным случаем описанных многоугольников.

Набор окружностей Джонсона состоит из трёх окружностей одинакового радиуса r, имеющих одну общую точку пересечения H. В такой конфигурации окружности обычно имеют четыре точки пересечения — это общая точка пересечения H, через которую проходят все три окружности, и по дополнительной точке для каждой пары окружностей. Если любые две окружности не пересекаются они имеют лишь одну общую точку — H, и в этом случае считается, что H является и их попарной точкой пересечения также. Если же окружности совпадают, принимается за попарную точку пересечения точка, диаметрально противоположная точке H. Три точки попарных пересечений окружностей Джонсона образуют опорный треугольник Δ ABC фигуры. Конфигурация названа именем Роджера Артура Джонсона.

Центр Шпикера — замечательная точка треугольника, определяемая как центр масс периметра треугольника; то есть центр тяжести однородной проволоки, проходящей по периметру треугольника.
Важной составной частью геометрии треугольника является теория фигур и кривых, вписанных в треугольник или описанных около него — окружностей, эллипсов и других.

Описанное коническое сечение или описанная коника для треугольника — это коническое сечение, проходящее через три вершины треугольника, а вписанное коническое сечение или вписанная коника — это вписанное в треугольник коническое сечение, т.е. касающееся сторон треугольника

Треугольник точек касания вневписанных окружностей треугольника образован соединением точек, в которых вневписанные окружности касаются треугольника. Для краткости в статье будем называть этот треугольник треугольником внекасаний.

Точка Фейербаха — точка касания вписанной окружности к окружности девяти точек треугольника. Точка Фейербаха является касательной точкой треугольника, что означает то, что её определение не зависит от расположения и размеров треугольника. Точка внесена с кодом X(11) в энциклопедию центров треугольника Кларка Кимберлинга и названа именем Карла Вильгельма Фейербаха.
























