Явление Макроскопического Квантования амплитуд

Явление Квантования Амплитуд Макроскопических Колебательных Систем возникает при взаимодействии по меньшей мере двух макроскопических колебательных систем, связь между которыми имеет особый фазово-зависимый характер [1][2][3][4][5][6][7][8][9][10][11][12][13][14][15][16][17][18][19][20][21][22][23][24][25][26][27][28][29]. Такое взаимодействие формирует условия возбуждения резонансных колебаний осцилляторов с дискретным рядом устойчивых квантованных амплитуд, которые принадлежат к новому классу – так называемым «аргументным колебаниям» [30][31][32][33][34][35][36][37][38][39][40][41].
Новые физические принципы привлекли внимание ученых и исследователей многих стран [42][43][44][45][46][47][48][49][50][50][51][52][53][54][55][56][57][58][59].
Это явление было открыто экспериментально Данилом и Яковом Дубошинскими в 1967 – 1968 годах.
Классическим примером, демонстрирующим явление квантования амплитуд, является аргументный (магнитный) маятник Дубошинского [44][60][61][62][63][64][65][66].
В физической энциклопедии аргументный (магнитный) маятник Дубошинского представлен достаточно подробно[67]. Поэтому ограничимся кратким описанием основных свойств и особенностей этого маятника, характеризующих рассматриваемое явление.
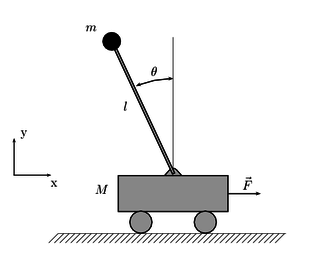
Устройство, принципиальная схема которого представлена на Рис. 1, состоит из механического маятника с низким трением, движущегося в вертикальной плоскости, на свободном конце которого закреплен небольшой постоянный магнит. Под самой низкой точкой движения маятника (эта точка определяется положением равновесия маятника) установлена индуктивная катушка (электромагнит), питаемая от источника переменного тока монохроматической частоты. Ось катушки электромагнита расположена горизонтально к плоскости движения маятника. Таким образом, в каждый момент времени электромагнит оказывает ускоряющее или замедляющее воздействие на магнит, закрепленный на свободном конце маятника, в зависимости от полярности тока в электромагните и от направления движения маятника. Ширина электромагнита должна быть меньше длины маятника, с таким расчетом, чтобы воздействие электромагнита на маятник было значительным лишь на небольшом отрезке траектории его движения, когда постоянный магнит находится в относительно небольшой зоне взаимодействия [-X0, X0], примерно соответствующей ширине электромагнита. Такая пространственная неоднородность поля, воздействующего на маятник, играет ключевую роль в возникновении явления квантования амплитуд.
Электромагнит соединяется с источником синусоидального переменного тока, частота Ω и амплитуда А которого могут варьироваться в широком диапазоне значений (обычно Ω от 20 до 3000 Гц при собственном периоде маятника порядка 0,5 Гц).
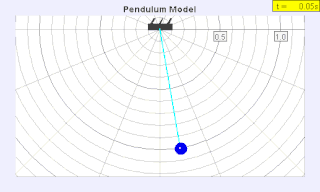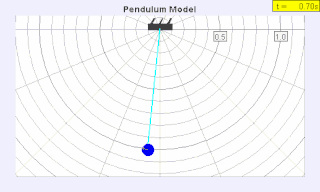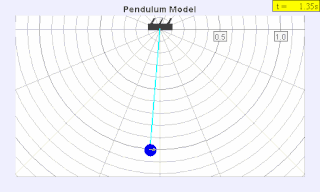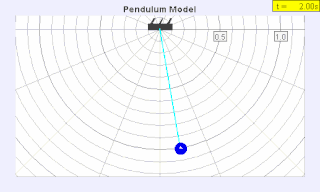
Приводя маятник в движение, легко наблюдать следующие особенности его поведения:
1. Из заданного начального положения маятник реализует устойчивый режим колебаний, квантованная амплитуда которого принимает одно из дискретного множества n возможных значений[15]:
где:
n = 2m + к, m = 0, 1, 2, ... , к = 1, 3, 5, ... ,
w0 - собственная частота колебаний осциллятора,
Ω - частота высокочастотного (или низкочастотного) воздействия.
Устойчивость каждой из квантованных амплитуд поддерживается фазовой самонастройкой между маятником и электромагнитом, аналогом которой является автофазировка Векслера – Макмиллана в приборах СВЧ и ускорителях заряженных частиц. В процессе взаимодействия с переменным полем электромагнита маятник извлекает такое количество энергии (порцию энергии), которая компенсирует его диссипативные потери энергии за каждый период (или ряд периодов) его колебаний.
2. Значения квантовых амплитуд и соответствующих порций поглощаемой маятником энергии для каждого устойчивого дискретного режима его колебаний практически не зависят от амплитуды А переменного тока, подаваемого на электромагнит, при ее изменении в очень большом диапазоне значений. При этом, механизм компенсации изменения напряженности магнитного поля электромагнита основан на саморегулируемом изменении фаз взаимодействия, что позволяет обеспечить устойчивые значения амплитуды и частоты колебаний маятника. Если постепенно снижать амплитуду тока, подаваемого на электромагнит, то достигается порог, ниже которого стабильный режим больше не будет поддерживаться, и маятник переместится на более низкий квантованный режим устойчивых колебаний.
3. Значения устойчивых квантовых амплитуд n колебаний маятника и их количество существенно зависят от частоты Ω переменного тока, питающего электромагнит. Чем выше частота Ω, тем большеe количество устойчивых амплитуд колебаний маятника, которые могут быть возбуждены.
4. Воспроизведение устойчивых квантовых амплитуд аргументным маятником связано с режимом резонансного обмена энергией [17] между механическим звеном и электромагнитом, который принципиально отличается от известного классического случая "вынужденных колебаний" осциллятора под действием периодической внешней силы. В классическом случае эффективный обмен энергией между осциллятором и внешним воздействием происходит только тогда, когда частота внешней силы совпадает с собственной частотой осциллятора или очень к ней близка. В случае аргументного маятника, устойчивые колебания реализуются, когда собственная частота w0 маятника и частота Ω внешнего воздействия могут отличаться на два и более порядка. При этом, в устойчивом режиме маятник всегда колеблется на частоте, близкой к его собственной частоте w0.
В соответствие с теорией аргументных колебаний, обобщенной в работах[2][13][15][29], были получены результаты, позволившие: сформулировать закон квантованного распределения расстояний планет и спутников планет солнечной системы[8][9][14]; сформулировать закон квантованного распределения частот биологических ритмов на планете Земля[68]; показать возможность вычисления квантованных амплитуд при взаимодействии СВЧ и лазерного излучений[2][7], осуществить генерацию энергии с дискретным спектром устойчивых амплитуд[34][35] и др.
Примечания
- ↑ Doubochinski D.B., Doubochinski J.B. et al. Quantification des amplitudes et de l'énergie absorbée par les systèmes oscillatoires macroscopiques sous l'action de la force périodique. Comptes rendus de la Xeme Conférence Internationale sur l'acoustique électronique. Tachkent, URSS, 1978.
- ↑ 1 2 3 Дубошинский Д.Б., Дубошинский Я.Б., Шабанский В.П. О дискретных стационарных колебаниях системы в поле неоднородной высокочастотной силы. ЖТФ, 49, 6, 1160, 1979. [Sov. Phys.-Tech. Phys. 24, 642(1979). USA].
- ↑ Дубошинский Д.Б., Дубошинский Я.Б О возбуждении волной колебаний осциллятора с дискретным рядом устойчивых амплитуд. ДАН СССР, 1982, т. 265, N°3, стр. 605 – 607; [Sov. Phys. Doklady 46, 149 (1982). USA].
- ↑ Doubochinski D.B., Doubochinski J.B., Damgov V.N. Absorption par l'oscillateur d'une portion d'énergie en interaction avec l'onde électromagnétique. Comptes-rendus de l'Académie Вulgare des Sciences, 1984, Vol. 37, No. 6, pp. 745 - 747.
- ↑ Doubochinski D.B., Doubochinski J.B., Damgov V.N., Amorçage des oscillations entretenues avec la série discrète des amplitudes stables. Comptes-rendus de l'Académie Bulgare des Sciences. Tome 39, No. 9, 1986.
- ↑ Doubochinski D.B., Doubochinski J.B. Amorçage argumentaire d'oscillations entretenues avec série discrète d'amplitudes stables. E.D.F.- BULLETIN de la direction des études et recherches - Série C, N°1, France. 1991.
- ↑ 1 2 Дубошинский Д.Б., Дубошинский Я.Б., Дамгов В.Н. Микроволновый генератор. Авторское свид. Болгарии № 80259, 1988.
- ↑ 1 2 Doubochinski D.B., Damgov V.N. On the wave nature and dynamical quantization (in the large) of the solar system planet and satellite arrangement. NASA ADS Astronomy Abstract Service. Report (ISSN 0861-1459), vol. 45, no. 2, 1992, p. 27-30.
- ↑ 1 2 Doubochinski D.B., Damgov V.N. The wave nature and dynamical quantization of the solar system. NASA ADS Astronomy Abstract Service. Earth, Moon, and Planets (ISSN 0167-9295), vol. 56, no. 3, March 1992, p. 233-242.
- ↑ Tennenbaum J. Amplitudes quantiques – une propriété élémentaire des systèmes vibratoires (découvert de Doubochinski). FUSION, La science, passionnément, N° 85, Paris, France. 2001.
- ↑ Tennenbaum J. Amplitudes Quantization – As an Elementary Property of Macroskopic Vibrating systems vibratoires. 21st CENTURY. SCIENCE & TECHNOLOGY. Winter 2005 – 2006.
- ↑ Doubochinski D., Tennenbaum J. Physique d’interaction: une nouvelle approche à la compréhension et à l'utilisation techniques des effets de quantification dans le macro- et micro-monde. Portail : International Scientifique Ecole de développement durable (numéro d'enregistrement d'état 0220712064). Une unité interdisciplinaire permanente «La science contemporaine", Octobre 21, 2006.
- ↑ 1 2 Doubochinski D., Tennenbaum J. The Macroscopic Quantum Effect in Nonlinear Oscillating Systems: a Possible Bridge between Classical and Quantum Physics. Cornell University Library «ARXIV», November 2007. Дата обращения: 12 сентября 2021. Архивировано 12 сентября 2021 года.
- ↑ 1 2 Дубошинский Д.Б. Макрофизичесая квантовая модель солнечной системы, SciTecLibrary, April 07, 2011. Дата обращения: 12 сентября 2021. Архивировано 12 сентября 2021 года.
- ↑ 1 2 3 Doubochinski D.B. Doubochinski’s Macrophysical Quantum Effect (DMQE): Experimental and Theoretical Argumentation. Monographe. Sciteclibrary, June 12, 2012. Дата обращения: 12 сентября 2021. Архивировано 12 сентября 2021 года.
- ↑ Doubochinski D.B. About relation between the continuous and discrete in Nature from the perspective of Doubochinski’s macrophysical quantum effect. SciTecLibrary. 2013. Дата обращения: 12 сентября 2021. Архивировано 12 сентября 2021 года.
- ↑ Дубошинский Д.Б. Аргументный резонанс Дубошинского. Sciteclibrary. Moscou. 2018. Дата обращения: 2 августа 2021. Архивировано 12 сентября 2021 года.
- ↑ Yao Luo, Wenkai Fan, Chenghao Feng, Sihui Wang, Yinlong Wang. Multi-stability in Doubochinski's Pendulum. Cornell University, ArXiv, 2019
- ↑ Cretin B., Vernier D. Quantized amplitudes in a nonlinear resonant electrical circuit. Cornell University Library «ARXIV», Jan. 8, 2008. Дата обращения: 12 сентября 2021. Архивировано 12 сентября 2021 года.
- ↑ Weldon J. Wilson. RECENT TALKS: Amplitude Quantization as a Fundamental Property of Coupled Oscillator Systems - Doubochinski's pendulum. Oklahoma University, 2012 - 2015. Дата обращения: 12 сентября 2021. Архивировано 12 сентября 2021 года.
- ↑ Jason Yeisley, Andrew McFarlin, Chris Conley, Chris Stewart. Disscovering Amplitude Quantization as an Elementary Property of Macroscopic Vibrating Systems through Doubochinski’s Pendulum. University of Central Oklahoma. 2014. Дата обращения: 12 сентября 2021. Архивировано 24 января 2015 года.
- ↑ Дубошинсий Д.Б. Явление квантования энергии в макросопических системах. SciTecLibrary. Москва, 27.01. 2021. Дата обращения: 12 сентября 2021. Архивировано 12 сентября 2021 года.
- ↑ Madsen, M.L., Andersen, J.E.V., Nielsen, Investigation of argumental oscillations of a physical pendulum. 2021. European Journal of Physics
- ↑ Thiago de Cacio Luchese, Marcelo Nunes Schneider. Dynamics of a physical pendulum with a magnet in the presence of a coil. Revista Brasileira de Ensino de Física. Rev. Bras. Ensino Fís. vol.42 São Paulo, Epub 25-Maio-2020
- ↑ Дубошинский Д.Б., Дубошинский Я.Б., Галкин Ю.В. Аргументные колебания. Ученые записки ВГПИ, Серия «Физика», Владимир, 1972. T. 40, Вып. 6, стp. 50 - 57
- ↑ Дубошинский Д.Б. и др, Возбуждение незатухающих асинхронных колебаний. Успехи Физических Наук. Т. 109, Вып. 402.1973 [Sov. Phys. Usp. 16, 158 (1973). USA].
- ↑ Дубошинский Д.Б., Дубошинский Я.Б., Ашкеназе С.И. Введение в физику аргументных колебаний. Сборник «Вопросы возбуждения незатухающих колебаний», N° 2. Владимир, 1974. Стр. 53 – 37.
- ↑ Doubochinski D.B. The argumental paradigm of bioeffective interactions. Sciteclibrary. 2019. Дата обращения: 2 августа 2021. Архивировано 12 сентября 2021 года.
- ↑ 1 2 Doubochinski D.B. Oscillations argumantaire, Maсro-physical quantum effect. Monograph. SciTechLibrary. Moscou, 2015. Дата обращения: 2 августа 2021. Архивировано 12 сентября 2021 года.
- ↑ Дубошинский Д.Б., Дубошинский Я.Б., Пеннер Д.И. Аргументные колебания. Известия АН СССР- Механика твердого тела, N° 1, 1975, c. 18 [Sov Phys. Isv. 7, 54(1975). USA].
- ↑ Дубошинский Д.Б., Турсунов Ш.С. Возбуждение аргументных колебаний в электрических системах. Межвузовский сборник научных трудов „Радиопомехи КНЧ диапазона и их природа“. Владимир, 1980. Стp. 59 - 64.
- ↑ Doubochinski D.B., Doubochinski J.B., Damgov V.N. Amorçage argumentaire des oscillations entretenues. Comptes‑rendus de l'Académie Bulgare des Sciences, 1984, Vol. 37, No. 5, pp. 586.
- ↑ Shumaev A.I. and Maizelis Z.A. Distribution functions of argumental oscillations of the Duboshinskiy pendulum. Journal of Applied Physics. 2017
- ↑ 1 2 Дубошинский Д.Б., Дубошинский Я.Б. и др. Способ возбуждения аргументных незатухающих колебаний. Авторское свидетельство No. 355598, СССР, декабрь 1972.
- ↑ 1 2 Дубошинский Д.Б., Дубошинский Я.Б. и др. Аргументный мотор с множеством скоростей. Сборник «Вопросы возбуждения незатухающих колебаний. N° 2, Владимир, СССР, 1974. Стр. 60 – 69.
- ↑ Дубошинский Д.Б., Турсунов Ш. Возбуждение аргументных колебаний в электрических системах. Межуниверситетский сборник «Радиопомехи в области низких частот и их происхождение». Vladimir, СССР, 1980, стр. 59 - 64.
- ↑ Дубошинский Д.Б. Введение в аргументную топологию взаимодействий (Об аогументно-связанной природе физических объектов). SciTecLibrary. Москва. 2019. Дата обращения: 2 августа 2021. Архивировано 12 сентября 2021 года.
- ↑ Дубошинский Д.Б. Новые принципы аргументной самоорганизации. Монография. SciTecLibrary. Москва, 26.09. 2020. Дата обращения: 2 августа 2021. Архивировано 12 сентября 2021 года.
- ↑ Doubochinski D.B. Doubochinski’s oscillator and equation of argumental oscillations. SciTecLibrary. Моscou. 2020. (недоступная ссылка)
- ↑ Дубошинсий Д.Б. Явление квантования энергии в макроскопических системах. SciTecLibrary. Москва, 27.01. 2021. Дата обращения: 12 сентября 2021. Архивировано 12 сентября 2021 года.
- ↑ Дубошинский Д.Б. Аргументная концепция взаимодействий – возможный мост между классической и квантовой физикой. SciTecLibrary. Москва, 13.04.2021. Дата обращения: 12 сентября 2021. Архивировано 12 сентября 2021 года.
- ↑ Daniel Cintra, Pierre Argoul. Nonlinear argumental oscillators: A few examples of modulation via spatial position. Journal jf Vibration and Control. 2016.
- ↑ Chandrashekar Ram. National Centre for Biological Sciences. June 2016 – August 2016 (3 months) Bangalore, Analyst at KPMG India: We designed and built an Argumental oscillator system, the so-called Doubochinski's Pendulum. (Mechanical & Electrical versions).
- ↑ 1 2 International Young Physicists Tournement. Word Scientific Publiching Company. 2018. Chapter 8, p.p. 107-118, 167: Doubochinski’s Pendulum. Дата обращения: 2 августа 2021. Архивировано 12 сентября 2021 года.
- ↑ College Physics. Volum 1; Books.google.be. 2017. Doubochinski’s pendulum
- ↑ Tranquillo Janisch. Construction and Characterization of a Doubochinski Pendulum (Bachelorvortrag). Univrsity of Zurich. Physik-Institut. Seminar in Physics. 2016.
- ↑ Chandrashekar Ram. National Centre for Biological Sciences. June 2016 – August 2016 (3 months) Bangalore, Analyst at KPMG India: We designed and built an Argumental oscillator system, the so-called Doubochinski's Pendulum. (Mechanical & Electrical versions).
- ↑ Pendulum in physic, Chapitre 4. 2017. Doubochinski’s Pandulum. Дата обращения: 2 августа 2021. Архивировано 12 сентября 2021 года.
- ↑ Files schematic of the doubochinski pendulum. Png. Indonezia. Oleh Indo Surat Diposting pada 5. 2018
- ↑ 1 2 Lan Ziheng, Chen Jiahao, Gao Yantai, et al. The principle of electromagnetic "quantum" pendulum, and its experimetal study. Mechanics in Engineering, China. 2016, 38(4): 471-475. Дата обращения: 2 августа 2021. Архивировано 12 сентября 2021 года.
- ↑ Bajaj N.K. The Physics of Waves and Oscillations. Doubochinski’s pendulum. A Text-book of Physics by Exum Percival Lewis. 2014. Дата обращения: 2 августа 2021. Архивировано 24 марта 2015 года.
- ↑ Martin Beech. The Pendulum Paradigm: Variations on a Theme and the Measure of Heaven and Earth. Brown Walker Press, USA. 2014. Doubochinski pendulum: p. 231-235, 242, 279.
- ↑ Mendel Gymnasium, Opava, contributory organization. Oscillatory modes of an excited nonlinear oscillator, § 3.9. Pendulum Doubochinski. Moravian-Silesian Region – The Czech Republiс, Opava – 2018. Дата обращения: 2 августа 2021. Архивировано 12 сентября 2021 года.
- ↑ Yao Luo. Subharmonic frequency response in a magnetic pendulum Doubochinski. American Journal of Physics 88, 115 (2020);
- ↑ Minghui Xu, Hang Li, Zaiqiao Bai. Magnetic Pendulum - Experimental Study on The Phase Locking of Magnetic Pendulum. Department of Physics, Beijing Normal University, Beijing, China. 2020. Дата обращения: 12 сентября 2021. Архивировано 12 сентября 2021 года.
- ↑ Krystian Polczyński, Adam Wijata, Jan Awrejcewicz. Theoretical and numerical analysis of different modes in a system of a “kicked” magnetic pendulum. Lodz University of Technology. Theor. Approaches Non-Linear Dyn. Syst. 2021.
- ↑ World Technologies. A Comprehensive Introduction to Pressure (Fundamental Physics Concept), Concepts of Mechanical Vibrations and Pendulum in Physics. Chapter 13, Page 44 Doubochinski's pendulum. Edition Ocean Media, 2021. Дата обращения: 12 сентября 2021. Архивировано 12 сентября 2021 года.
- ↑ Henrik B Pedersen, Magnus Linnet Madsen, John E V Andersen. Investigation of argumental oscillations of a physical pendulum. 10 February 2021. European Physical Society. European Journal of Physics, Volume 42, Number 2.
- ↑ Doubochinski’s Pendulum. World History. 15 Apr. 2021, Discovery Media. Дата обращения: 2 августа 2021. Архивировано 12 сентября 2021 года.
- ↑ Базовый маятник Дубошинского. Дата обращения: 2 августа 2021. Архивировано 12 сентября 2021 года.
- ↑ Магнитный маятник Дубошинского. Международный конкурс старшеклассников, 2018 год. Видео: снято для задачи турнира юных физиков 2015 года "Магнитный маятник" командой "СШ №1 г. п. Смиловичи" (Беларусь). Дата обращения: 12 сентября 2021. Архивировано 12 сентября 2021 года.
- ↑ DOUBLE TRIPLE OR MULTIPLE DOUBOCHINSKI PENDULUMS. Дата обращения: 12 сентября 2021. Архивировано 12 сентября 2021 года.
- ↑ Стохастический (хаотический) маятник Дубошинского
- ↑ Магнитный маятник Дубошинского, Часть 1. Физика в опытах и экспериментах.
- ↑ Магнитный маятник Дубошинского, Часть 2.
- ↑ College Physics. Volum 1; Books.google.be. 2017. Doubochinski’s pendulum.
- ↑ Словари и энциклопедии на Академике. Маятник Дубошинского.
- ↑ Дубошинский Д.Б. Аргументная парадигма биоэффективных взаимодействий. Sciteclibrary. 2019. Дата обращения: 2 августа 2021. Архивировано 12 сентября 2021 года.
![{\displaystyle a_{n}\approx {\sqrt {8\cdot [1-({\frac {\Omega }{n\omega _{0}}})^{2})]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91a444c29a5117449fa1072f1571cbae4867a999)