3,4-дуопризма
Однородные 3,4-дуопризмы 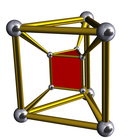 Диаграммы Шлегеля | |
|---|---|
| Тип | Призматический однородный 4-мерный многогранник[англ.] |
| Символ Шлефли | |
| Диаграмма Коксетера — Дынкина | |
| Ячеек | 3 квадратных призмы, 4 треугольные призмы |
| Граней | 15 квадратов, 4 треугольника |
| Рёбер | 24 |
| Вершин | 12 |
| Вершинная фигура |  Дигональный дисфеноид[англ.] |
| Симметрия[англ.] | [3,2,4], порядок 48 |
| Двойственный многогранник | 3,4-дуопирамида |
| Свойства | выпуклый, вершинно транзитивен |
3,4-дуопризма — вторая из наименьших -дуопризм, четырёхмерный многогранник, получающийся в результате прямого произведения треугольника и квадрата. Существует в некоторых однородных 5-многогранниках в семействе B5[англ.].
Изображения
 Развёртка |  3D-проекция с 3 различными вращениями |
Связанные комплексные многогранники

Квазиправильный комплексный многогранник , ![]()
![]()
![]() , в пространстве имеет вещественное представление как 3,4-дуопризма в четырёхмерном пространстве. Он имеет 12 вершин и 4 3-ребра и 3 4-ребра. Его симметрия равна , порядок симметрии 12[1].
, в пространстве имеет вещественное представление как 3,4-дуопризма в четырёхмерном пространстве. Он имеет 12 вершин и 4 3-ребра и 3 4-ребра. Его симметрия равна , порядок симметрии 12[1].
Связанные многогранники
Биспрямлённый 5-куб[англ.], ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() имеет однородную 3,4-дуопризму в качестве вершинной фигуре:
имеет однородную 3,4-дуопризму в качестве вершинной фигуре:
3,4-дуопирамида
| 3,4-дуопирамида | |
|---|---|
| Тип | Дуопирамида[англ.] |
| Символ Шлефли | {3}+{4} |
| Диаграмма Коксетера — Дынкина | |
| Ячеек | 12 Дигональный дисфеноид[англ.] |
| Гранией | 24 равнобедренных треугольника |
| Рёбер | 19 (12+3+4) |
| Вершин | 7 (3+4) |
| Симметрия[англ.] | [3,2,4], порядок 48 |
| Двойственный многогранник | 3,4-дуопризма |
| Свойства | выпуклый, гране транзитивный |
Двойственный многогранник 3,4-дуопризмы называется 3,4-дуопирамидой[англ.]. Он имеет 12 ячеек в виде дигонального дисфеноида[англ.], 24 грани в виде равнобедренных граней, 12 рёбер и 7 вершин.
 Ортогональная проекция |  Вершинно-центрированная перспектива |
См. также
Примечания
Литература
- Coxeter H. S. M. Regular Complex Polytopes. — Cambridge University Press, 1974.
- Coxeter H. S. M. Regular Polytopes. — New York: Dover Publications, Inc., 1973. — С. 124.
- Coxeter H. S. M. Chapter 5: Regular Skew Polyhedra in three and four dimensions and their topological analogues // The Beauty of Geometry: Twelve Essays. — Dover Publications, 1999. — ISBN 0-486-40919-8.
- Coxeter H. S. M. Regular Skew Polyhedra in Three and Four Dimensions // Proc. London Math. Soc.. — 1937. — Вып. 43. — С. 33—62.
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass. Chapter 26 // The Symmetries of Things. — 2008. — ISBN 978-1-56881-220-5.
- Norman Johnson. Uniform Polytopes. — 1991. — (Рукопись).
- N.W. Johnson. The Theory of Uniform Polytopes and Honeycombs. — University of Toronto, 1966. — (Ph.D. Dissertation).
Ссылки
- The Fourth Dimension Simply Explained описывает дуопризмы как «двойные призмы» и дуоцилиндры как "двойные цилиндры"
- Polygloss — словарь терминов пространств высокой размерности
- Exploring Hyperspace with the Geometric Product




![{\displaystyle _{3}[2]_{4}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b512f8aa95c5415e6f55c23de009fd284274432f)