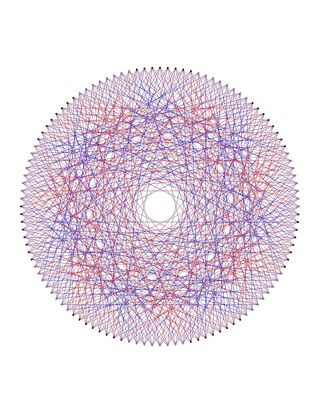
3-регулярный граф Клейна

3-регулярный граф Кляйна

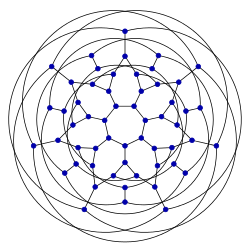Назван в честь	Феликс Кляйн
Вершин	56
Рёбер	84
Радиус	6
Диаметр	6
Обхват	7
Автоморфизмы	336
Хроматическое число	3
Хроматический индекс	3
Свойства	симметричный кубический гамильтонов граф Кэли
Книжная толщина	3
Число очередей	2

3-регулярный граф Клейна — кубический граф с 56 вершинами и 84 рёбрами; назван по имени Феликса Клейна с двойственным ему 7-регулярным графом.

Граф гамильтонов, имеет хроматическое число 3, хроматический индекс 3, радиус 6, диаметр 6 и обхват 7. Является также вершинно 3-связным и рёберно 3-связным. Имеет толщину книги 3 и Число очередей 2^[1].

Граф, как и двойственный ему 7-регулярный, можно вложить в ориентируемую поверхность рода 3, где он образует карту с 24 семиугольными гранями. Символ Шлефли — {7,3}₈.

Согласно списку Фостера, где граф обозначен как F056B, является единственным кубическим симметричным графом с 56 вершинами, который не является двудольным^[2].

Может быть получен из графа Коксетера с 28 вершинами^[3].

Группой автоморфизмов 3-регулярного графа Клейна является группа PGL₂(7) порядка 336, которая имеет PSL₂(7) в качестве нормальной подгруппы. Эта группа действует транзитивно на полурёбра, так что граф Кляйна является симметричным.

Характеристическим многочленом этого графа с 56 вершинами является:

x^{7}\,(x-3)\,(x+2)^{6}\left(x^{2}-2\right)^{6}\left(x^{2}+x-4\right)^{7}\left(x^{2}-2x-1\right)^{8}

Гамильтонов путь, раскрашенный в 3 цвета рёбер (что показывает хроматический индекс, равный 3)

Литература

Jessica Wolz. Engineering Linear Layouts with SAT. — University of Tübingen, 2018. — (Master Thesis).
Conder M., Dobcsányi P. Trivalent symmetric graphs up to 768 vertices // J. Combin. Math. Combin. Comput.. — 2002. — Т. 40. — С. 41–63.
Italo Dejter. From the Coxeter graph to the Klein graph // CiteSeer. — 2010. — arXiv:1002.1960.
Egon Schulte, Wills J. M. A Polyhedral Realization of Felix Klein's Map {3, 7}₈ on a Riemann Surface of Genus 3 // J. London Math. Soc.. — 1985. — Т. s2-32, вып. 3. — С. 539–547. — doi:10.1112/jlms/s2-32.3.539.
Andries Brouwer, Arjeh Cohen, Arnold Neumaier. Distance-Regular Graphs. — Springer-Verlag, 1989. — С. 398. — ISBN 978-0-387-50619-7.
van Dam E. R., Haemers W. H., Koolen J. H., Spence E. Characterizing distance-regularity of graphs by the spectrum // J. Combin. Theory Ser. A. — 2006. — Т. 113, вып. 8. — С. 1805–1820. — doi:10.1016/j.jcta.2006.03.008.

Похожие исследовательские статьи

Граф Хивуда — ненаправленный граф с 14 вершинами и 21 ребром, названный в честь Перси Джона Хивуда.

Симметричный граф (или транзитивный относительно дуг граф) — граф G, для любых двух пар смежных вершин которого u₁—v₁ и u₂—v₂ имеется автоморфизм:

f : V(G) → V(G)

<span class="mw-page-title-main">Дистанционно-транзитивный граф</span> такой граф, что для любых двух заданных вершин v и w, находящихся на расстоянии i, и любых двух вершин x и y, находящихся на том же расстоянии, су

Дистанционно-транзитивный граф — граф, в котором любая упорядоченная пара вершин переводится в любую другую упорядоченную пару вершин с тем же расстоянием между вершинами одним из автоморфизмов графа.

В теории графов графом Паппа называется двудольный 3-регулярный неориентированный граф с 18 вершинами и 27 рёбрами, являющийся графом Леви конфигурации Паппа. Он назван в честь Паппа Александрийского, математика Древней Греции, который верил, что доказал «теорему о шестиугольнике», в которой описывал конфигурацию Паппа. Все кубические дистанционно-регулярные графы известны. Граф Паппа — один из тринадцати таких графов.

Граф Дика — 3-регулярный граф с 32 вершинами и 48 рёбрами, назван в честь Вальтера фон Дика .

Граф Фостера — двудольный 3-регулярный граф с 90 вершинами и 135 рёбрами. Граф Фостера является гамильтоновым, имеет хроматическое число 2, хроматический индекс 3, радиус 8, диаметр 8 и обхват 10. Также является вершинно 3-связным и рёберно 3-связным.

Граф Биггса — Смита — 3-регулярный граф с 102 вершинами и 153 рёбрами. Назван в честь Биггса и Смита, описавших граф в 1971 году.

Граф Коксетера — 3-регулярный граф с 28 вершинами и 42 рёбрам Все кубические дистанционно-регулярные графы известны, граф Коксетера — один из 13-ти таких графов.

В теории графов граф Науру — это симметричный двудольный кубический граф с 24 вершинами и 36 рёбрами. Граф был назван Дэвидом Эпштейном по аналогии с двенадцатилучевой звездой на флаге Науру.

Граф F26A — симметричный двудольный кубический граф с 26 вершинами и 39 рёбрами.

В теории графов граф Харриса или (3-10)-клетка Харриса — это 3-регулярный неориентированный граф с 70 вершинами и 105 рёбрами.

Граф Хортона — 3-регулярный граф с 96 вершинами и 144 рёбрами, открытый Джозефом Хортоном. Бонди и Мурти опубликовали в 1976 этот граф в качестве контрпримера гипотезе Татта, что любой кубический 3-связный двудольный граф является гамильтоновым.

12-клетка Татта — 3-регулярный граф с 126 вершинами и 189 рёбрами, названный в честь Уильяма Татта.

Граф Любляны — неориентированный двудольный граф с 112 вершинами и 168 рёбрами.

Граф Фолкмана — это двудольный 4-регулярный граф с 20 вершинами и 40 рёбрами.

Граф Шрикханде — граф, найденный С. С. Шрикханде в 1959 году. Граф сильно регулярен, имеет 16 вершин и 48 рёбер и каждая вершина имеет степень 6. Каждая пара узлов имеет ровно два общих соседа, независимо от того, связана эта пара ребром или нет.

Граф Хоффмана является 4-регулярным графом с 16 вершинами и 32 рёбрами, который открыл Алан Хоффман и опубликовал в 1963. Граф коспектрален графу гиперкуба Q₄.

Граф Мередита — 4-регулярный неориентированный граф с 70 вершинами и 140 рёбрами, обнаруженный Гаем Мередитом в 1973 году.

<span class="mw-page-title-main">Граф Деджтера</span>

Граф Деджтера — это 6-регулярный граф с 112 вершинами, 336 рёбрами и обхватом 4. Граф Деджтера получается путём удаления копии кода Хэмминга длины 7 из бинарного 7-куба.

7-регулярный граф Клейна — регулярный граф степени 7 с 24 вершинами и 84 рёбрами; назван, наряду с двойственным ему 3-регулярным графом, по имени Феликса Клейна.

Эта страница основана на статье Википедии.
Текст доступен на условиях лицензии CC BY-SA 4.0; могут применяться дополнительные условия.
Изображения, видео и звуки доступны по их собственным лицензиям.